HSDF-Lane: Height-Aligned Signed Distance Field with Semantic Lane Prior for 3D Lane Detection

Monocular 3D lane detection plays a critical role in autonomous driving, yet recovering reliable 3D geometry from a single image remains challenging due to inherent depth ambiguity. Prior methods project image features into Bird's-Eye-View (BEV) space under a flat-ground assumption, causing geometric distortion on real-world roads. Recent methods instead predict explicit height maps to capture non-planar surfaces, but still rely on sparse anchor-based regression and exploit the recovered geometry merely for spatial transformation rather than semantic understanding. To overcome these limitations, we propose HSDF-Lane, which implicitly models the road surface as a Height-aligned Signed Distance Field (HSDF) over a densely sampled 3D feature volume. Through differentiable rendering, the HSDF jointly produces an accurate height map and surface-aligned features. We further introduce Lane-aware Semantic Positional Encoding (LSPE), which injects a lane-existence prior derived from the surface-aligned features into the transformer queries, coupling geometric structure with semantic guidance. Extensive experiments on the OpenLane benchmark show that HSDF-Lane achieves state-of-the-art performance in both 3D lane detection and height map estimation.

Stable Surface Regularization for Fast Few-Shot NeRF

This paper proposes an algorithm for synthesizing novel views under few-shot setup. The main concept is to develop a stable surface regularization technique called Annealing Signed Distance Function (ASDF), which anneals the surface in a coarse-to-fine manner to accelerate convergence speed. We observe that the Eikonal loss - which is a widely known geometric regularization - requires dense training signal to shape different level-sets of SDF, leading to low-fidelity results under few-shot training. In contrast, the proposed surface regularization successfully reconstructs scenes and produce high-fidelity geometry with stable training. Our method is further accelerated by utilizing grid representation and monocular geometric priors. Finally, the proposed approach is up to 45 times faster than existing few-shot novel view synthesis methods, and it produces comparable results in the ScanNet dataset and NeRF-Real dataset.

Deep Point Cloud Reconstruction

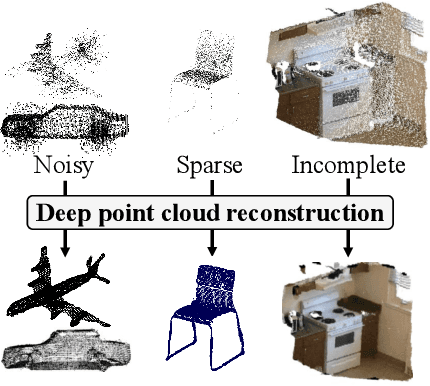
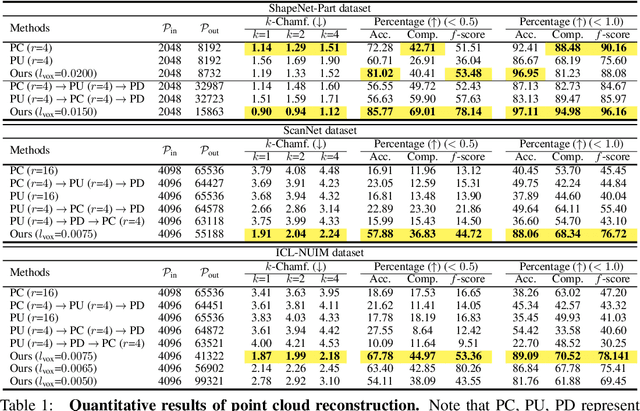
Point cloud obtained from 3D scanning is often sparse, noisy, and irregular. To cope with these issues, recent studies have been separately conducted to densify, denoise, and complete inaccurate point cloud. In this paper, we advocate that jointly solving these tasks leads to significant improvement for point cloud reconstruction. To this end, we propose a deep point cloud reconstruction network consisting of two stages: 1) a 3D sparse stacked-hourglass network as for the initial densification and denoising, 2) a refinement via transformers converting the discrete voxels into 3D points. In particular, we further improve the performance of transformer by a newly proposed module called amplified positional encoding. This module has been designed to differently amplify the magnitude of positional encoding vectors based on the points' distances for adaptive refinements. Extensive experiments demonstrate that our network achieves state-of-the-art performance among the recent studies in the ScanNet, ICL-NUIM, and ShapeNetPart datasets. Moreover, we underline the ability of our network to generalize toward real-world and unmet scenes.