Nonlinear Multi-objective Reinforcement Learning with Provable Guarantees

We describe RA-E3 (Reward-Aware Explicit Explore or Exploit), an algorithm with provable guarantees for solving a single or multi-objective Markov Decision Process (MDP) where we want to maximize the expected value of a nonlinear function over accumulated rewards. This allows us to model fairness-aware welfare optimization for multi-objective reinforcement learning as well as risk-aware reinforcement learning with nonlinear Von Neumann-Morgenstern utility functions in the single objective setting. RA-E3 extends the classic E3 algorithm that solves MDPs with scalar rewards and linear preferences. We first state a distinct reward-aware version of value iteration that calculates a non-stationary policy that is approximately optimal for a given model of the environment. This sub-procedure is based on an extended form of Bellman optimality for nonlinear optimization that explicitly considers time and current accumulated reward. We then describe how to use this optimization procedure in a larger algorithm that must simultaneously learn a model of the environment. The algorithm learns an approximately optimal policy in time that depends polynomially on the MDP size, desired approximation, and smoothness of the nonlinear function, and exponentially on the number of objectives.

Do Not Harm Protected Groups in Debiasing Language Representation Models

Language Representation Models (LRMs) trained with real-world data may capture and exacerbate undesired bias and cause unfair treatment of people in various demographic groups. Several techniques have been investigated for applying interventions to LRMs to remove bias in benchmark evaluations on, for example, word embeddings. However, the negative side effects of debiasing interventions are usually not revealed in the downstream tasks. We propose xGAP-DEBIAS, a set of evaluations on assessing the fairness of debiasing. In this work, We examine four debiasing techniques on a real-world text classification task and show that reducing biasing is at the cost of degrading performance for all demographic groups, including those the debiasing techniques aim to protect. We advocate that a debiasing technique should have good downstream performance with the constraint of ensuring no harm to the protected group.

Welfare and Fairness in Multi-objective Reinforcement Learning

We study fair multi-objective reinforcement learning in which an agent must learn a policy that simultaneously achieves high reward on multiple dimensions of a vector-valued reward. Motivated by the fair resource allocation literature, we model this as an expected welfare maximization problem, for some non-linear fair welfare function of the vector of long-term cumulative rewards. One canonical example of such a function is the Nash Social Welfare, or geometric mean, the log transform of which is also known as the Proportional Fairness objective. We show that even approximately optimal optimization of the expected Nash Social Welfare is computationally intractable even in the tabular case. Nevertheless, we provide a novel adaptation of Q-learning that combines non-linear scalarized learning updates and non-stationary action selection to learn effective policies for optimizing nonlinear welfare functions. We show that our algorithm is provably convergent, and we demonstrate experimentally that our approach outperforms techniques based on linear scalarization, mixtures of optimal linear scalarizations, or stationary action selection for the Nash Social Welfare Objective.

Proportionally Fair Clustering

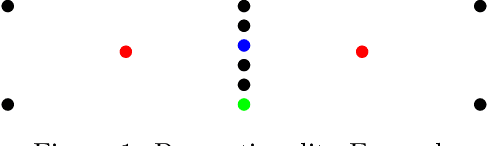
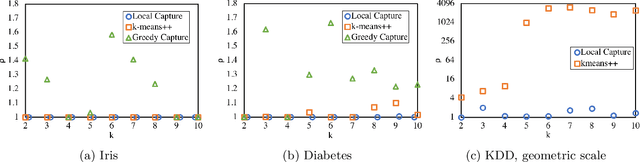
We extend the fair machine learning literature by considering the problem of proportional centroid clustering in a metric context. For clustering $n$ points with $k$ centers, we define fairness as proportionality to mean that any $n/k$ points are entitled to form their own cluster if there is another center that is closer in distance for all $n/k$ points. We seek clustering solutions to which there are no such justified complaints from any subsets of agents, without assuming any a priori notion of protected subsets. We present and analyze algorithms to efficiently compute, optimize, and audit proportional solutions. We conclude with an empirical examination of the tradeoff between proportional solutions and the $k$-means objective.

Random Dictators with a Random Referee: Constant Sample Complexity Mechanisms for Social Choice

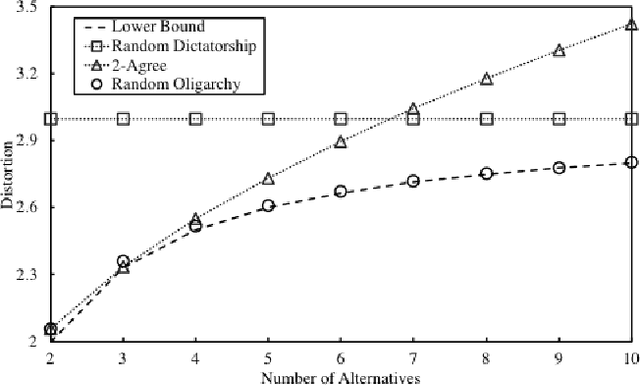
We study social choice mechanisms in an implicit utilitarian framework with a metric constraint, where the goal is to minimize \textit{Distortion}, the worst case social cost of an ordinal mechanism relative to underlying cardinal utilities. We consider two additional desiderata: Constant sample complexity and Squared Distortion. Constant sample complexity means that the mechanism (potentially randomized) only uses a constant number of ordinal queries regardless of the number of voters and alternatives. Squared Distortion is a measure of variance of the Distortion of a randomized mechanism. Our primary contribution is the first social choice mechanism with constant sample complexity \textit{and} constant Squared Distortion (which also implies constant Distortion). We call the mechanism Random Referee, because it uses a random agent to compare two alternatives that are the favorites of two other random agents. We prove that the use of a comparison query is necessary: no mechanism that only elicits the top-k preferred alternatives of voters (for constant k) can have Squared Distortion that is sublinear in the number of alternatives. We also prove that unlike any top-k only mechanism, the Distortion of Random Referee meaningfully improves on benign metric spaces, using the Euclidean plane as a canonical example. Finally, among top-1 only mechanisms, we introduce Random Oligarchy. The mechanism asks just 3 queries and is essentially optimal among the class of such mechanisms with respect to Distortion. In summary, we demonstrate the surprising power of constant sample complexity mechanisms generally, and just three random voters in particular, to provide some of the best known results in the implicit utilitarian framework.