Batch Effects In Brain Foundation Model Embeddings

Foundation models show strong potential for large-scale, high-dimensional biomedical applications, yet their ability to capture relevant neurobiological characteristics remains underexplored. We systematically evaluate embeddings from two neuroimaging foundation models, BrainLM and SwiFT, across multi-site fMRI datasets using a comprehensive evaluation framework. Our results show that foundation model embeddings encode substantial batch-related variability, often dominating diagnosis-related information across heterogeneous datasets. We further investigate how harmonization, applied to reduce batch effects, influences these embeddings. In addition, we find that BrainLM prefers to capture fine-grained regional activity, whereas SwiFT tends to represent interactions between regions, consistent with their respective model architectures. Our study highlights the importance of accounting for batch effects in foundation models and motivates future work on disentangling biologically meaningful signals from acquisition-related variability.

Spectral Introspection Identifies Group Training Dynamics in Deep Neural Networks for Neuroimaging

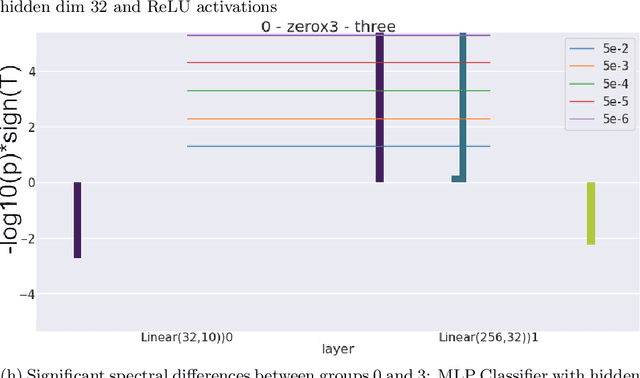
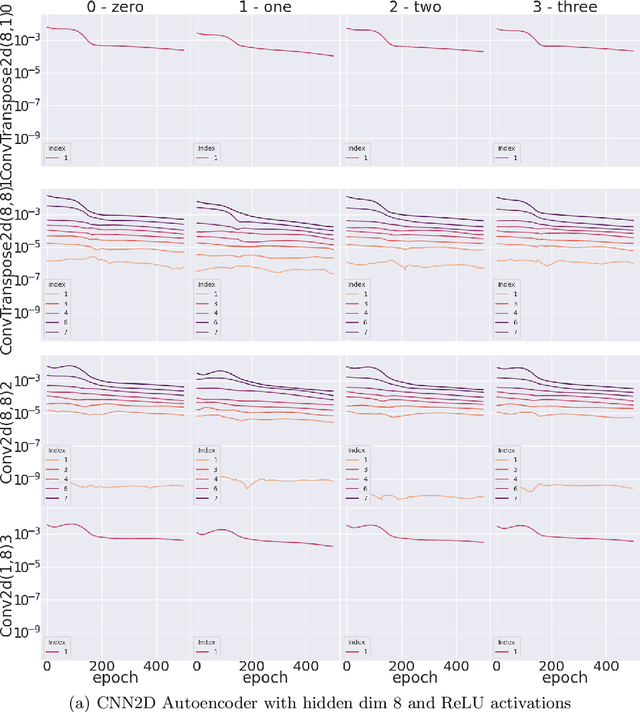
Neural networks, whice have had a profound effect on how researchers study complex phenomena, do so through a complex, nonlinear mathematical structure which can be difficult for human researchers to interpret. This obstacle can be especially salient when researchers want to better understand the emergence of particular model behaviors such as bias, overfitting, overparametrization, and more. In Neuroimaging, the understanding of how such phenomena emerge is fundamental to preventing and informing users of the potential risks involved in practice. In this work, we present a novel introspection framework for Deep Learning on Neuroimaging data, which exploits the natural structure of gradient computations via the singular value decomposition of gradient components during reverse-mode auto-differentiation. Unlike post-hoc introspection techniques, which require fully-trained models for evaluation, our method allows for the study of training dynamics on the fly, and even more interestingly, allow for the decomposition of gradients based on which samples belong to particular groups of interest. We demonstrate how the gradient spectra for several common deep learning models differ between schizophrenia and control participants from the COBRE study, and illustrate how these trajectories may reveal specific training dynamics helpful for further analysis.

Multiscale Neuroimaging Features for the Identification of Medication Class and Non-Responders in Mood Disorder Treatment

In the clinical treatment of mood disorders, the complex behavioral symptoms presented by patients and variability of patient response to particular medication classes can create difficulties in providing fast and reliable treatment when standard diagnostic and prescription methods are used. Increasingly, the incorporation of physiological information such as neuroimaging scans and derivatives into the clinical process promises to alleviate some of the uncertainty surrounding this process. Particularly, if neural features can help to identify patients who may not respond to standard courses of anti-depressants or mood stabilizers, clinicians may elect to avoid lengthy and side-effect-laden treatments and seek out a different, more effective course that might otherwise not have been under consideration. Previously, approaches for the derivation of relevant neuroimaging features work at only one scale in the data, potentially limiting the depth of information available for clinical decision support. In this work, we show that the utilization of multi spatial scale neuroimaging features - particularly resting state functional networks and functional network connectivity measures - provide a rich and robust basis for the identification of relevant medication class and non-responders in the treatment of mood disorders. We demonstrate that the generated features, along with a novel approach for fast and automated feature selection, can support high accuracy rates in the identification of medication class and non-responders as well as the identification of novel, multi-scale biomarkers.

Low-Rank Learning by Design: the Role of Network Architecture and Activation Linearity in Gradient Rank Collapse

Our understanding of learning dynamics of deep neural networks (DNNs) remains incomplete. Recent research has begun to uncover the mathematical principles underlying these networks, including the phenomenon of "Neural Collapse", where linear classifiers within DNNs converge to specific geometrical structures during late-stage training. However, the role of geometric constraints in learning extends beyond this terminal phase. For instance, gradients in fully-connected layers naturally develop a low-rank structure due to the accumulation of rank-one outer products over a training batch. Despite the attention given to methods that exploit this structure for memory saving or regularization, the emergence of low-rank learning as an inherent aspect of certain DNN architectures has been under-explored. In this paper, we conduct a comprehensive study of gradient rank in DNNs, examining how architectural choices and structure of the data effect gradient rank bounds. Our theoretical analysis provides these bounds for training fully-connected, recurrent, and convolutional neural networks. We also demonstrate, both theoretically and empirically, how design choices like activation function linearity, bottleneck layer introduction, convolutional stride, and sequence truncation influence these bounds. Our findings not only contribute to the understanding of learning dynamics in DNNs, but also provide practical guidance for deep learning engineers to make informed design decisions.

Efficient Distributed Auto-Differentiation

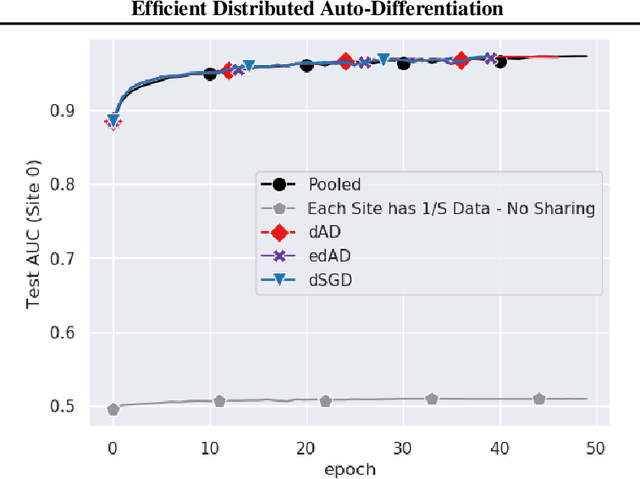
Although distributed machine learning has opened up numerous frontiers of research, the separation of large models across different devices, nodes, and sites can invite significant communication overhead, making reliable training difficult. The focus on gradients as the primary shared statistic during training has led to a number of intuitive algorithms for distributed deep learning; however, gradient-based algorithms for training large deep neural networks (DNNs) are communication-heavy, often requiring additional modifications via sparsity constraints, compression, quantization, and other similar approaches, to lower bandwidth. We introduce a surprisingly simple statistic for training distributed DNNs that is more communication-friendly than the gradient. The error backpropagation process can be modified to share these smaller intermediate values instead of the gradient, reducing communication overhead with no impact on accuracy. The process provides the flexibility of averaging gradients during backpropagation, enabling novel flexible training schemas while leaving room for further bandwidth reduction via existing gradient compression methods. Finally, consideration of the matrices used to compute the gradient inspires a new approach to compression via structured power iterations, which can not only reduce bandwidth but also enable introspection into distributed training dynamics, without significant performance loss.