Low-Rank Learning by Design: the Role of Network Architecture and Activation Linearity in Gradient Rank Collapse
Paper and Code
Feb 09, 2024
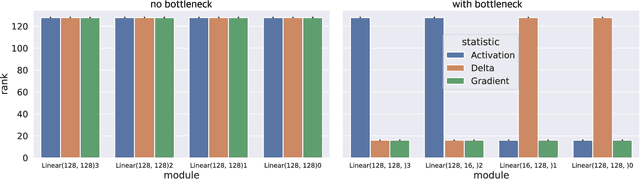

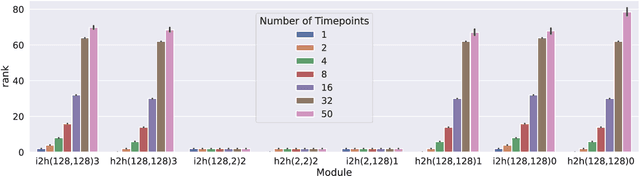
Our understanding of learning dynamics of deep neural networks (DNNs) remains incomplete. Recent research has begun to uncover the mathematical principles underlying these networks, including the phenomenon of "Neural Collapse", where linear classifiers within DNNs converge to specific geometrical structures during late-stage training. However, the role of geometric constraints in learning extends beyond this terminal phase. For instance, gradients in fully-connected layers naturally develop a low-rank structure due to the accumulation of rank-one outer products over a training batch. Despite the attention given to methods that exploit this structure for memory saving or regularization, the emergence of low-rank learning as an inherent aspect of certain DNN architectures has been under-explored. In this paper, we conduct a comprehensive study of gradient rank in DNNs, examining how architectural choices and structure of the data effect gradient rank bounds. Our theoretical analysis provides these bounds for training fully-connected, recurrent, and convolutional neural networks. We also demonstrate, both theoretically and empirically, how design choices like activation function linearity, bottleneck layer introduction, convolutional stride, and sequence truncation influence these bounds. Our findings not only contribute to the understanding of learning dynamics in DNNs, but also provide practical guidance for deep learning engineers to make informed design decisions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge