WisWheat: A Three-Tiered Vision-Language Dataset for Wheat Management

Wheat management strategies play a critical role in determining yield. Traditional management decisions often rely on labour-intensive expert inspections, which are expensive, subjective and difficult to scale. Recently, Vision-Language Models (VLMs) have emerged as a promising solution to enable scalable, data-driven management support. However, due to a lack of domain-specific knowledge, directly applying VLMs to wheat management tasks results in poor quantification and reasoning capabilities, ultimately producing vague or even misleading management recommendations. In response, we propose WisWheat, a wheat-specific dataset with a three-layered design to enhance VLM performance on wheat management tasks: (1) a foundational pretraining dataset of 47,871 image-caption pairs for coarsely adapting VLMs to wheat morphology; (2) a quantitative dataset comprising 7,263 VQA-style image-question-answer triplets for quantitative trait measuring tasks; and (3) an Instruction Fine-tuning dataset with 4,888 samples targeting biotic and abiotic stress diagnosis and management plan for different phenological stages. Extensive experimental results demonstrate that fine-tuning open-source VLMs (e.g., Qwen2.5 7B) on our dataset leads to significant performance improvements. Specifically, the Qwen2.5 VL 7B fine-tuned on our wheat instruction dataset achieves accuracy scores of 79.2% and 84.6% on wheat stress and growth stage conversation tasks respectively, surpassing even general-purpose commercial models such as GPT-4o by a margin of 11.9% and 34.6%.

SCORE: Soft Label Compression-Centric Dataset Condensation via Coding Rate Optimization

Dataset Condensation (DC) aims to obtain a condensed dataset that allows models trained on the condensed dataset to achieve performance comparable to those trained on the full dataset. Recent DC approaches increasingly focus on encoding knowledge into realistic images with soft labeling, for their scalability to ImageNet-scale datasets and strong capability of cross-domain generalization. However, this strong performance comes at a substantial storage cost which could significantly exceed the storage cost of the original dataset. We argue that the three key properties to alleviate this performance-storage dilemma are informativeness, discriminativeness, and compressibility of the condensed data. Towards this end, this paper proposes a \textbf{S}oft label compression-centric dataset condensation framework using \textbf{CO}ding \textbf{R}at\textbf{E} (SCORE). SCORE formulates dataset condensation as a min-max optimization problem, which aims to balance the three key properties from an information-theoretic perspective. In particular, we theoretically demonstrate that our coding rate-inspired objective function is submodular, and its optimization naturally enforces low-rank structure in the soft label set corresponding to each condensed data. Extensive experiments on large-scale datasets, including ImageNet-1K and Tiny-ImageNet, demonstrate that SCORE outperforms existing methods in most cases. Even with 30$\times$ compression of soft labels, performance decreases by only 5.5\% and 2.7\% for ImageNet-1K with IPC 10 and 50, respectively. Code will be released upon paper acceptance.

Color-Oriented Redundancy Reduction in Dataset Distillation

Dataset Distillation (DD) is designed to generate condensed representations of extensive image datasets, enhancing training efficiency. Despite recent advances, there remains considerable potential for improvement, particularly in addressing the notable redundancy within the color space of distilled images. In this paper, we propose AutoPalette, a framework that minimizes color redundancy at the individual image and overall dataset levels, respectively. At the image level, we employ a palette network, a specialized neural network, to dynamically allocate colors from a reduced color space to each pixel. The palette network identifies essential areas in synthetic images for model training and consequently assigns more unique colors to them. At the dataset level, we develop a color-guided initialization strategy to minimize redundancy among images. Representative images with the least replicated color patterns are selected based on the information gain. A comprehensive performance study involving various datasets and evaluation scenarios is conducted, demonstrating the superior performance of our proposed color-aware DD compared to existing DD methods. The code is available at \url{https://github.com/KeViNYuAn0314/AutoPalette}.

An Efficient Newton Method for Extreme Similarity Learning with Nonlinear Embeddings

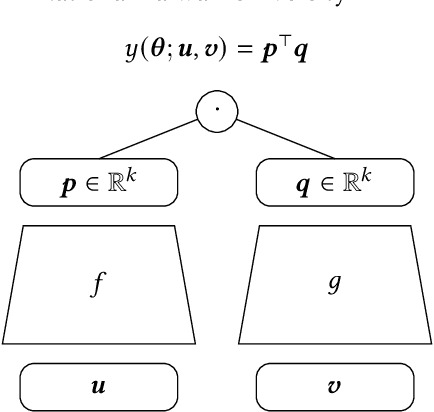
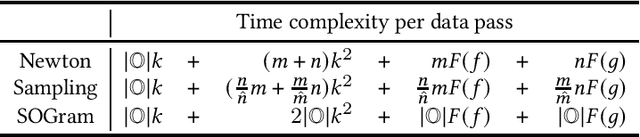
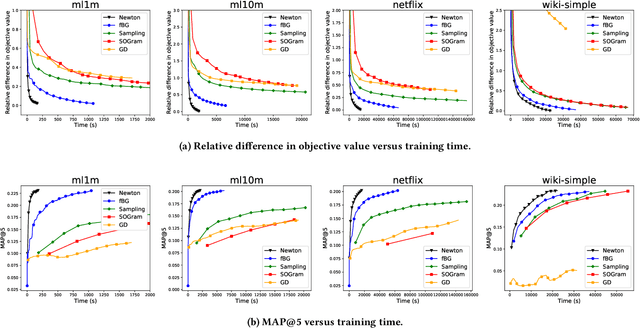
We study the problem of learning similarity by using nonlinear embedding models (e.g., neural networks) from all possible pairs. This problem is well-known for its difficulty of training with the extreme number of pairs. Existing optimization methods extended from stochastic gradient methods suffer from slow convergence and high complexity per pass of all possible pairs. Inspired by some recent works reporting that Newton methods are competitive for training certain types of neural networks, in this work, we novelly apply the Newton method for this problem. A prohibitive cost depending on the extreme number of pairs occurs if the Newton method is directly applied. We propose an efficient algorithm which successfully eliminates the cost. Our proposed algorithm can take advantage of second-order information and lower time complexity per pass of all possible pairs. Experiments conducted on large-scale data sets demonstrate that the proposed algorithm is more efficient than existing algorithms.