Boris Mitavskiy
A Polynomial Time Approximation Scheme for a Single Machine Scheduling Problem Using a Hybrid Evolutionary Algorithm
Apr 22, 2014Abstract:Nowadays hybrid evolutionary algorithms, i.e, heuristic search algorithms combining several mutation operators some of which are meant to implement stochastically a well known technique designed for the specific problem in question while some others playing the role of random search, have become rather popular for tackling various NP-hard optimization problems. While empirical studies demonstrate that hybrid evolutionary algorithms are frequently successful at finding solutions having fitness sufficiently close to the optimal, many fewer articles address the computational complexity in a mathematically rigorous fashion. This paper is devoted to a mathematically motivated design and analysis of a parameterized family of evolutionary algorithms which provides a polynomial time approximation scheme for one of the well-known NP-hard combinatorial optimization problems, namely the "single machine scheduling problem without precedence constraints". The authors hope that the techniques and ideas developed in this article may be applied in many other situations.
Combining Drift Analysis and Generalized Schema Theory to Design Efficient Hybrid and/or Mixed Strategy EAs
Apr 15, 2014Abstract:Hybrid and mixed strategy EAs have become rather popular for tackling various complex and NP-hard optimization problems. While empirical evidence suggests that such algorithms are successful in practice, rather little theoretical support for their success is available, not mentioning a solid mathematical foundation that would provide guidance towards an efficient design of this type of EAs. In the current paper we develop a rigorous mathematical framework that suggests such designs based on generalized schema theory, fitness levels and drift analysis. An example-application for tackling one of the classical NP-hard problems, the "single-machine scheduling problem" is presented.
A Theoretical Assessment of Solution Quality in Evolutionary Algorithms for the Knapsack Problem
Apr 14, 2014Abstract:Evolutionary algorithms are well suited for solving the knapsack problem. Some empirical studies claim that evolutionary algorithms can produce good solutions to the 0-1 knapsack problem. Nonetheless, few rigorous investigations address the quality of solutions that evolutionary algorithms may produce for the knapsack problem. The current paper focuses on a theoretical investigation of three types of (N+1) evolutionary algorithms that exploit bitwise mutation, truncation selection, plus different repair methods for the 0-1 knapsack problem. It assesses the solution quality in terms of the approximation ratio. Our work indicates that the solution produced by pure strategy and mixed strategy evolutionary algorithms is arbitrarily bad. Nevertheless, the evolutionary algorithm using helper objectives may produce 1/2-approximation solutions to the 0-1 knapsack problem.
Geiringer Theorems: From Population Genetics to Computational Intelligence, Memory Evolutive Systems and Hebbian Learning
May 11, 2013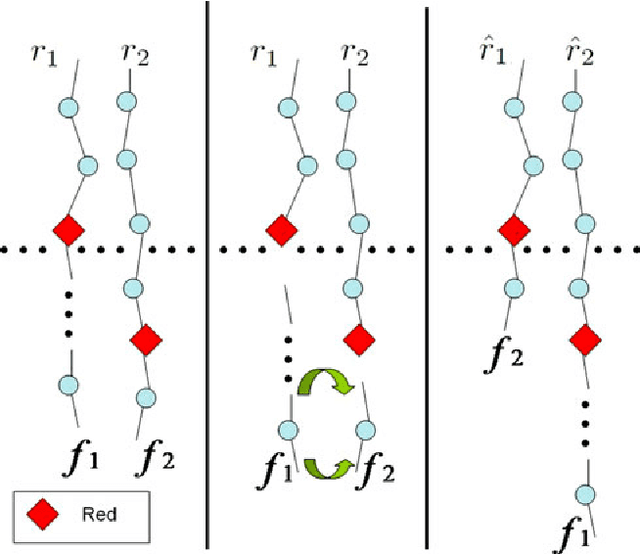
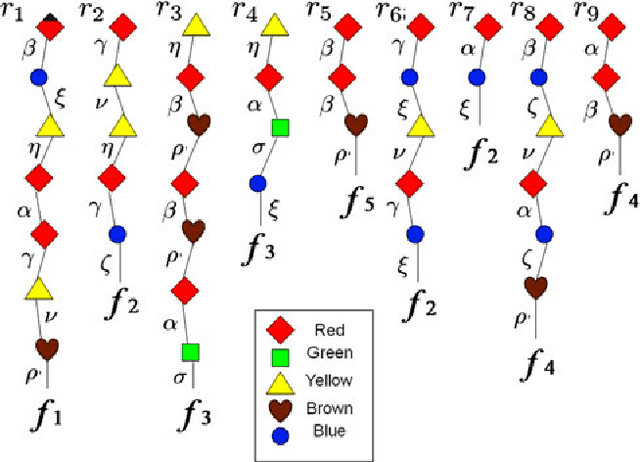
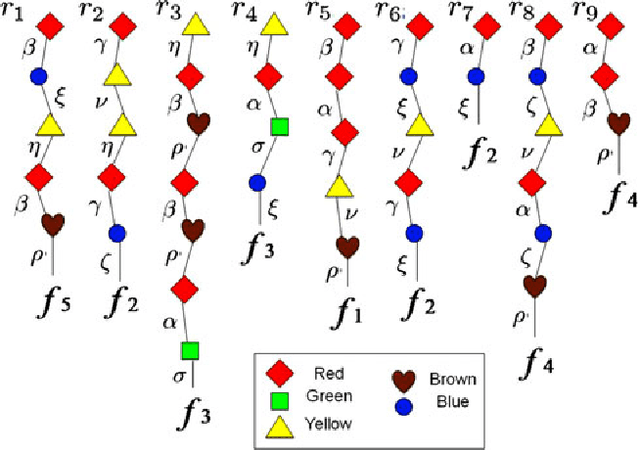
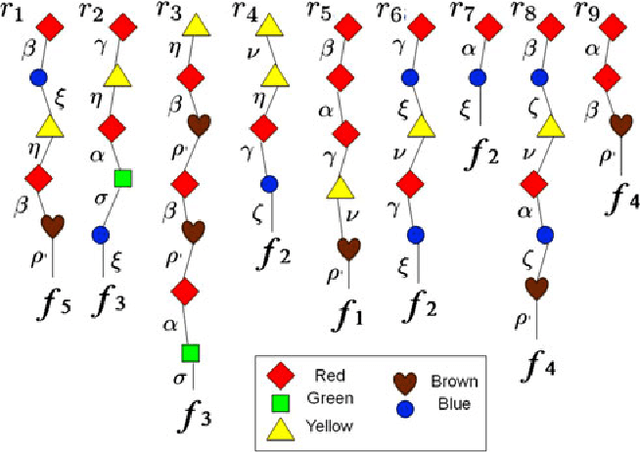
Abstract:The classical Geiringer theorem addresses the limiting frequency of occurrence of various alleles after repeated application of crossover. It has been adopted to the setting of evolutionary algorithms and, a lot more recently, reinforcement learning and Monte-Carlo tree search methodology to cope with a rather challenging question of action evaluation at the chance nodes. The theorem motivates novel dynamic parallel algorithms that are explicitly described in the current paper for the first time. The algorithms involve independent agents traversing a dynamically constructed directed graph that possibly has loops. A rather elegant and profound category-theoretic model of cognition in biological neural networks developed by a well-known French mathematician, professor Andree Ehresmann jointly with a neurosurgeon, Jan Paul Vanbremeersch over the last thirty years provides a hint at the connection between such algorithms and Hebbian learning.
* arXiv admin note: text overlap with arXiv:1110.4657
A Further Generalization of the Finite-Population Geiringer-like Theorem for POMDPs to Allow Recombination Over Arbitrary Set Covers
May 11, 2013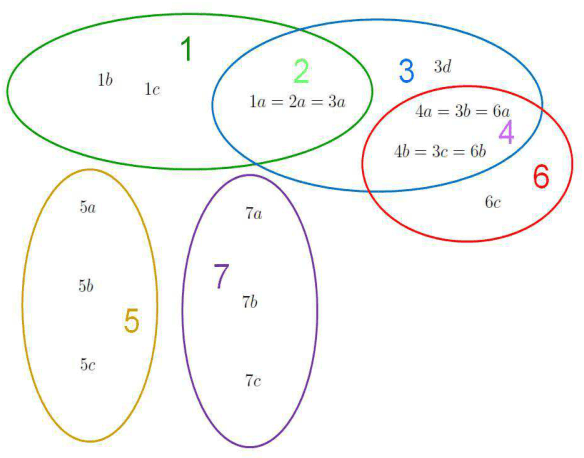
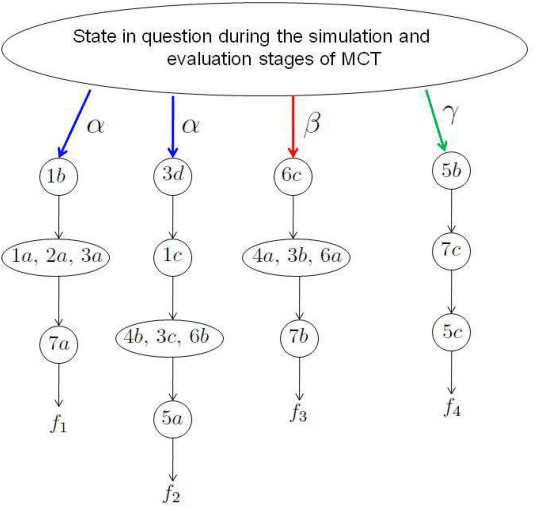
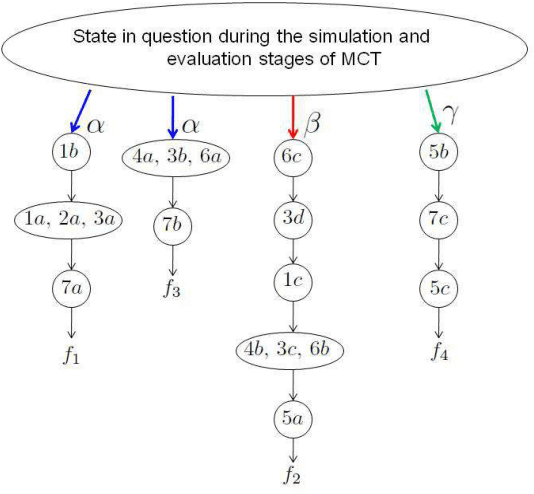
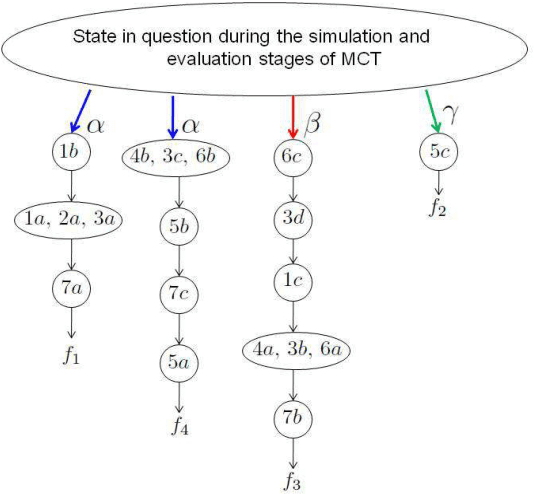
Abstract:A popular current research trend deals with expanding the Monte-Carlo tree search sampling methodologies to the environments with uncertainty and incomplete information. Recently a finite population version of Geiringer theorem with nonhomologous recombination has been adopted to the setting of Monte-Carlo tree search to cope with randomness and incomplete information by exploiting the entrinsic similarities within the state space of the problem. The only limitation of the new theorem is that the similarity relation was assumed to be an equivalence relation on the set of states. In the current paper we lift this "curtain of limitation" by allowing the similarity relation to be modeled in terms of an arbitrary set cover of the set of state-action pairs.
Novel Analysis of Population Scalability in Evolutionary Algorithms
May 10, 2013



Abstract:Population-based evolutionary algorithms (EAs) have been widely applied to solve various optimization problems. The question of how the performance of a population-based EA depends on the population size arises naturally. The performance of an EA may be evaluated by different measures, such as the average convergence rate to the optimal set per generation or the expected number of generations to encounter an optimal solution for the first time. Population scalability is the performance ratio between a benchmark EA and another EA using identical genetic operators but a larger population size. Although intuitively the performance of an EA may improve if its population size increases, currently there exist only a few case studies for simple fitness functions. This paper aims at providing a general study for discrete optimisation. A novel approach is introduced to analyse population scalability using the fundamental matrix. The following two contributions summarize the major results of the current article. (1) We demonstrate rigorously that for elitist EAs with identical global mutation, using a lager population size always increases the average rate of convergence to the optimal set; and yet, sometimes, the expected number of generations needed to find an optimal solution (measured by either the maximal value or the average value) may increase, rather than decrease. (2) We establish sufficient and/or necessary conditions for the superlinear scalability, that is, when the average convergence rate of a $(\mu+\mu)$ EA (where $\mu\ge2$) is bigger than $\mu$ times that of a $(1+1)$ EA.
A Version of Geiringer-like Theorem for Decision Making in the Environments with Randomness and Incomplete Information
Oct 20, 2011
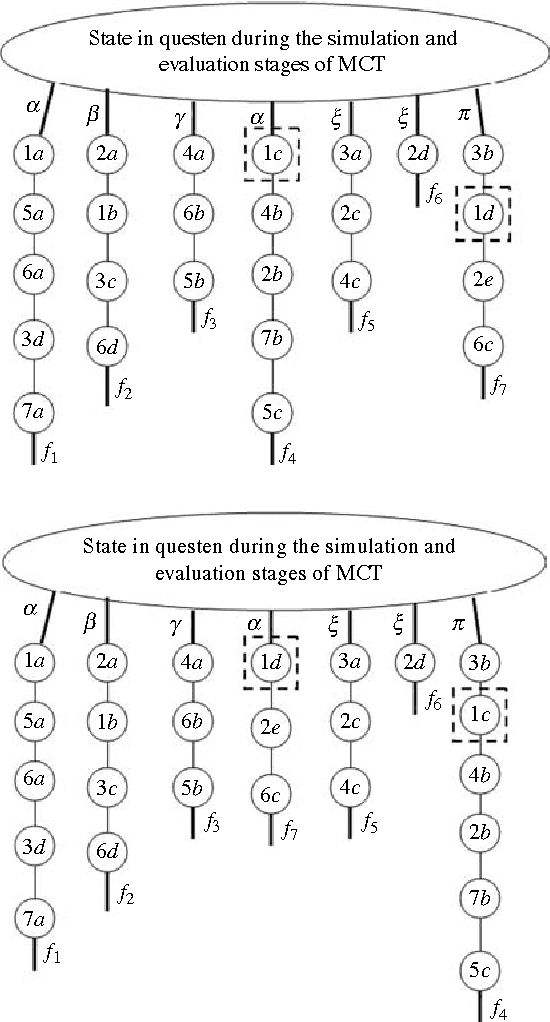

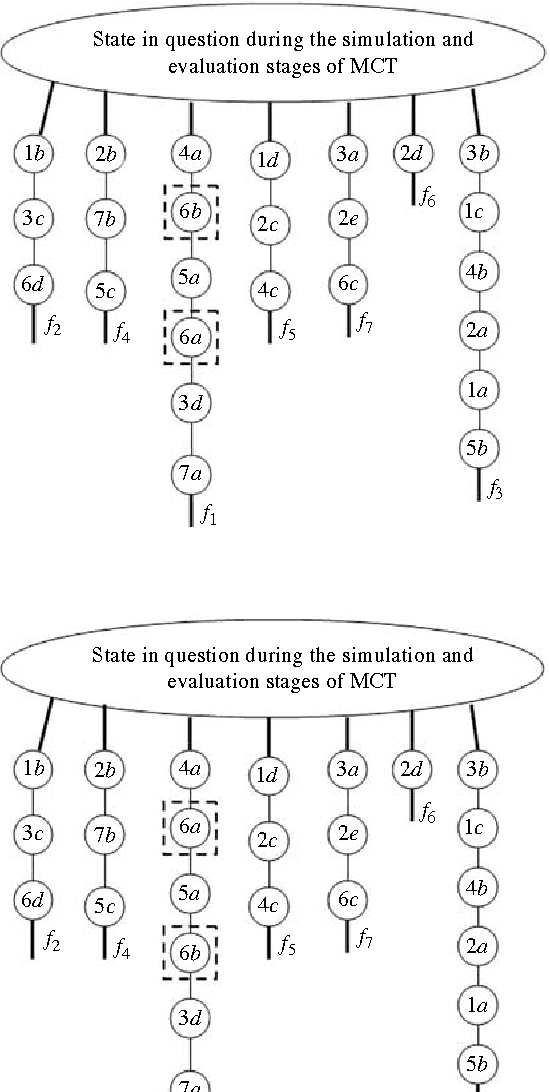
Abstract:Purpose: In recent years Monte-Carlo sampling methods, such as Monte Carlo tree search, have achieved tremendous success in model free reinforcement learning. A combination of the so called upper confidence bounds policy to preserve the "exploration vs. exploitation" balance to select actions for sample evaluations together with massive computing power to store and to update dynamically a rather large pre-evaluated game tree lead to the development of software that has beaten the top human player in the game of Go on a 9 by 9 board. Much effort in the current research is devoted to widening the range of applicability of the Monte-Carlo sampling methodology to partially observable Markov decision processes with non-immediate payoffs. The main challenge introduced by randomness and incomplete information is to deal with the action evaluation at the chance nodes due to drastic differences in the possible payoffs the same action could lead to. The aim of this article is to establish a version of a theorem that originated from population genetics and has been later adopted in evolutionary computation theory that will lead to novel Monte-Carlo sampling algorithms that provably increase the AI potential. Due to space limitations the actual algorithms themselves will be presented in the sequel papers, however, the current paper provides a solid mathematical foundation for the development of such algorithms and explains why they are so promising.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge