Jonathan Rowe
Geiringer Theorems: From Population Genetics to Computational Intelligence, Memory Evolutive Systems and Hebbian Learning
May 11, 2013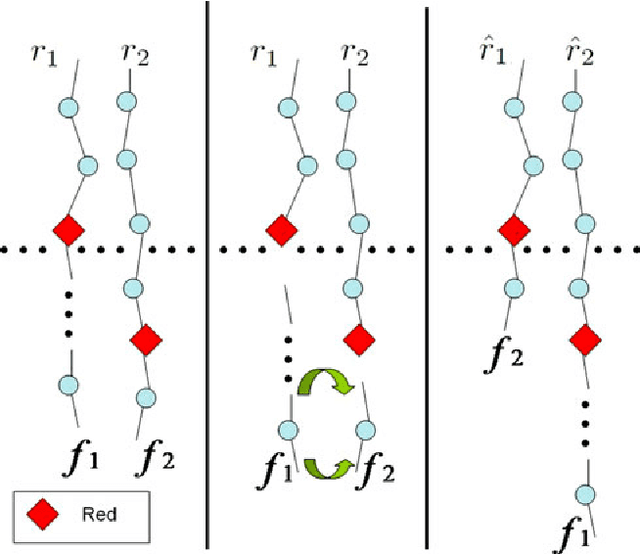
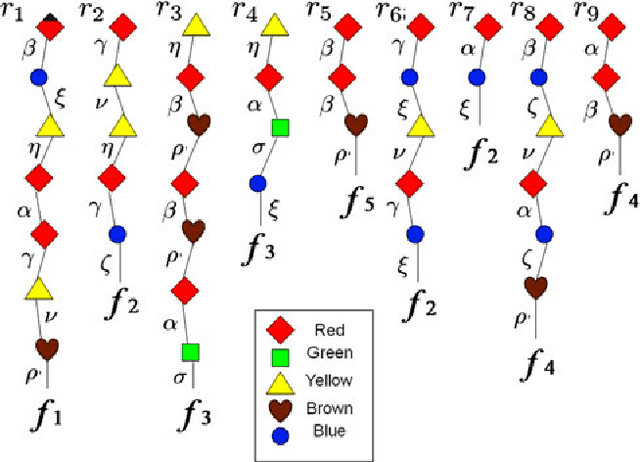
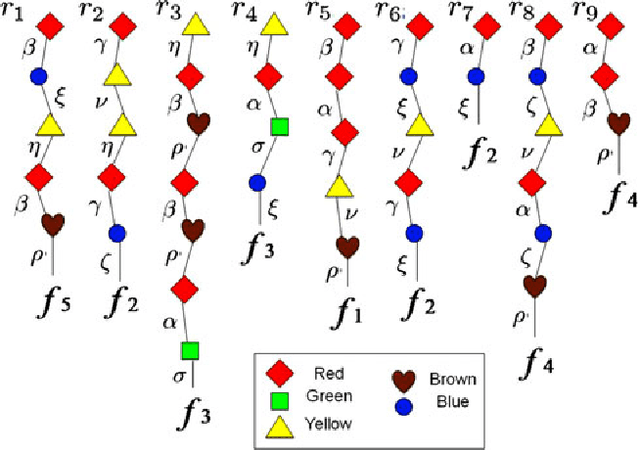
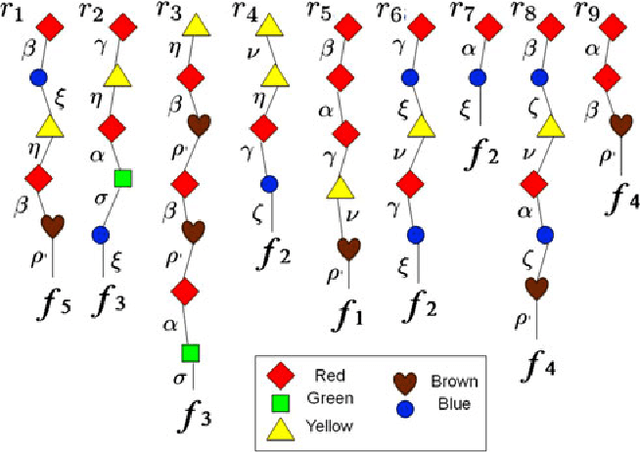
Abstract:The classical Geiringer theorem addresses the limiting frequency of occurrence of various alleles after repeated application of crossover. It has been adopted to the setting of evolutionary algorithms and, a lot more recently, reinforcement learning and Monte-Carlo tree search methodology to cope with a rather challenging question of action evaluation at the chance nodes. The theorem motivates novel dynamic parallel algorithms that are explicitly described in the current paper for the first time. The algorithms involve independent agents traversing a dynamically constructed directed graph that possibly has loops. A rather elegant and profound category-theoretic model of cognition in biological neural networks developed by a well-known French mathematician, professor Andree Ehresmann jointly with a neurosurgeon, Jan Paul Vanbremeersch over the last thirty years provides a hint at the connection between such algorithms and Hebbian learning.
* arXiv admin note: text overlap with arXiv:1110.4657
A Version of Geiringer-like Theorem for Decision Making in the Environments with Randomness and Incomplete Information
Oct 20, 2011
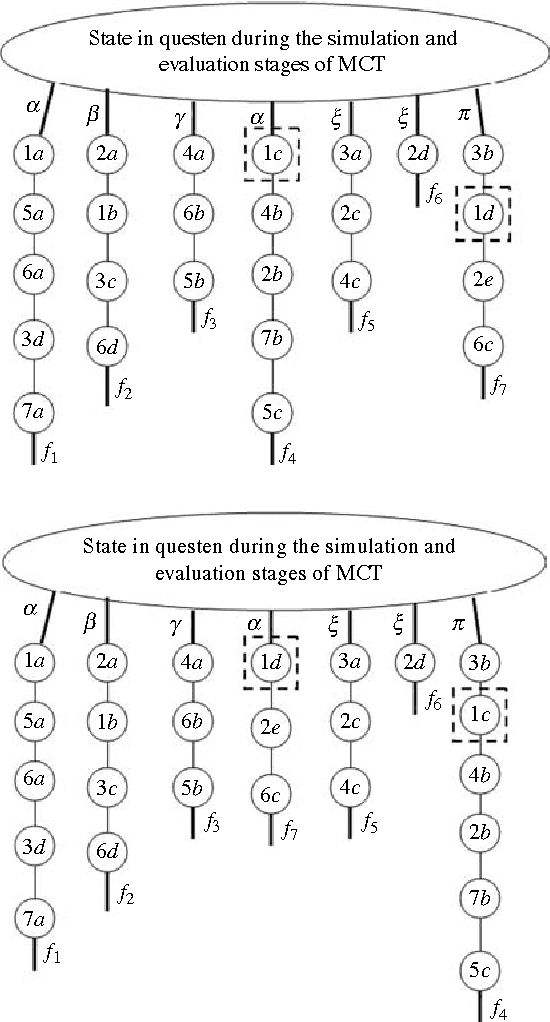

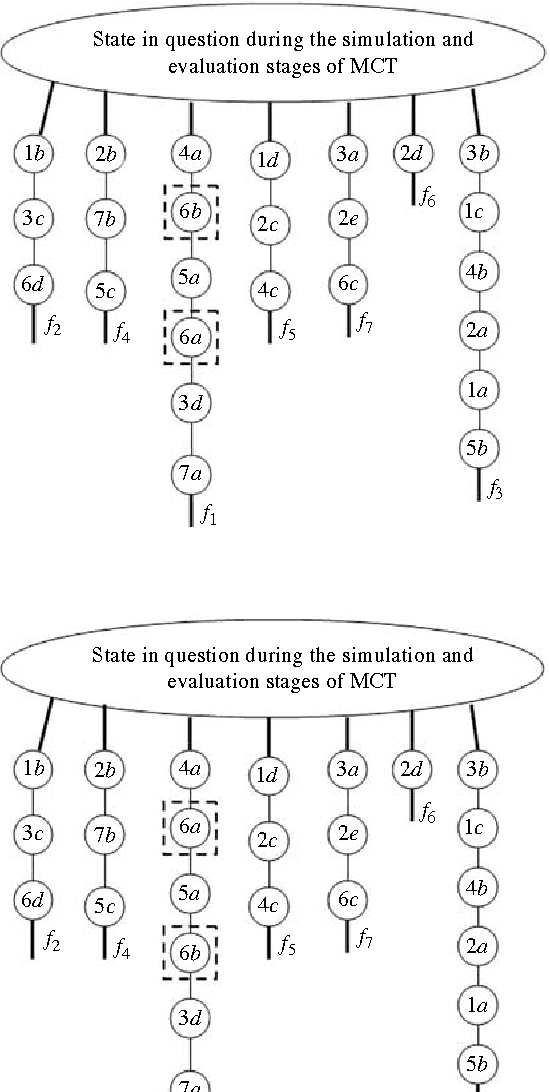
Abstract:Purpose: In recent years Monte-Carlo sampling methods, such as Monte Carlo tree search, have achieved tremendous success in model free reinforcement learning. A combination of the so called upper confidence bounds policy to preserve the "exploration vs. exploitation" balance to select actions for sample evaluations together with massive computing power to store and to update dynamically a rather large pre-evaluated game tree lead to the development of software that has beaten the top human player in the game of Go on a 9 by 9 board. Much effort in the current research is devoted to widening the range of applicability of the Monte-Carlo sampling methodology to partially observable Markov decision processes with non-immediate payoffs. The main challenge introduced by randomness and incomplete information is to deal with the action evaluation at the chance nodes due to drastic differences in the possible payoffs the same action could lead to. The aim of this article is to establish a version of a theorem that originated from population genetics and has been later adopted in evolutionary computation theory that will lead to novel Monte-Carlo sampling algorithms that provably increase the AI potential. Due to space limitations the actual algorithms themselves will be presented in the sequel papers, however, the current paper provides a solid mathematical foundation for the development of such algorithms and explains why they are so promising.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge