Don't trust your eyes: on the reliability of feature visualizations

How do neural networks extract patterns from pixels? Feature visualizations attempt to answer this important question by visualizing highly activating patterns through optimization. Today, visualization methods form the foundation of our knowledge about the internal workings of neural networks, as a type of mechanistic interpretability. Here we ask: How reliable are feature visualizations? We start our investigation by developing network circuits that trick feature visualizations into showing arbitrary patterns that are completely disconnected from normal network behavior on natural input. We then provide evidence for a similar phenomenon occurring in standard, unmanipulated networks: feature visualizations are processed very differently from standard input, casting doubt on their ability to "explain" how neural networks process natural images. We underpin this empirical finding by theory proving that the set of functions that can be reliably understood by feature visualization is extremely small and does not include general black-box neural networks. Therefore, a promising way forward could be the development of networks that enforce certain structures in order to ensure more reliable feature visualizations.

Impossibility Theorems for Feature Attribution

Despite a sea of interpretability methods that can produce plausible explanations, the field has also empirically seen many failure cases of such methods. In light of these results, it remains unclear for practitioners how to use these methods and choose between them in a principled way. In this paper, we show that for even moderately rich model classes (easily satisfied by neural networks), any feature attribution method that is complete and linear--for example, Integrated Gradients and SHAP--can provably fail to improve on random guessing for inferring model behaviour. Our results apply to common end-tasks such as identifying local model behaviour, spurious feature identification, and algorithmic recourse. One takeaway from our work is the importance of concretely defining end-tasks. In particular, we show that once such an end-task is defined, a simple and direct approach of repeated model evaluations can outperform many other complex feature attribution methods.

Adaptively Exploiting d-Separators with Causal Bandits

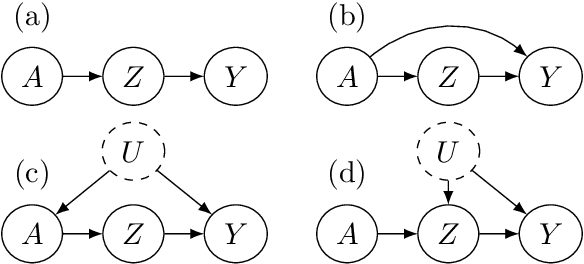
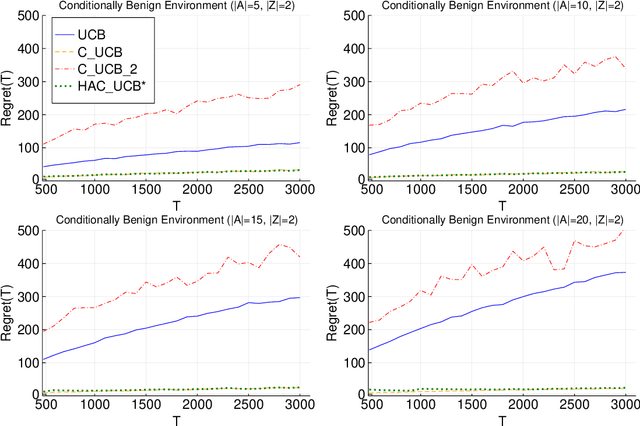
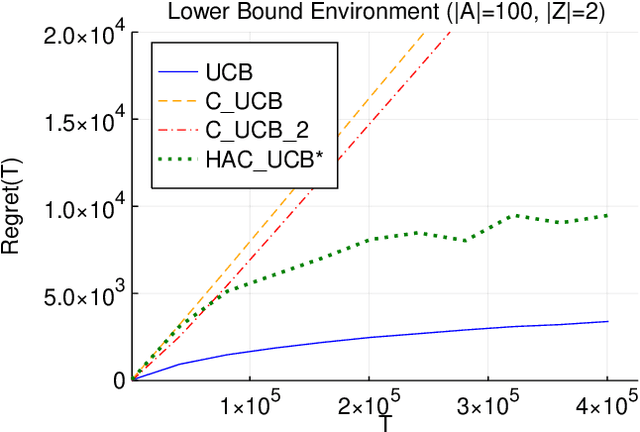
Multi-armed bandit problems provide a framework to identify the optimal intervention over a sequence of repeated experiments. Without additional assumptions, minimax optimal performance (measured by cumulative regret) is well-understood. With access to additional observed variables that d-separate the intervention from the outcome (i.e., they are a d-separator), recent causal bandit algorithms provably incur less regret. However, in practice it is desirable to be agnostic to whether observed variables are a d-separator. Ideally, an algorithm should be adaptive; that is, perform nearly as well as an algorithm with oracle knowledge of the presence or absence of a d-separator. In this work, we formalize and study this notion of adaptivity, and provide a novel algorithm that simultaneously achieves (a) optimal regret when a d-separator is observed, improving on classical minimax algorithms, and (b) significantly smaller regret than recent causal bandit algorithms when the observed variables are not a d-separator. Crucially, our algorithm does not require any oracle knowledge of whether a d-separator is observed. We also generalize this adaptivity to other conditions, such as the front-door criterion.

Minimax Optimal Quantile and Semi-Adversarial Regret via Root-Logarithmic Regularizers

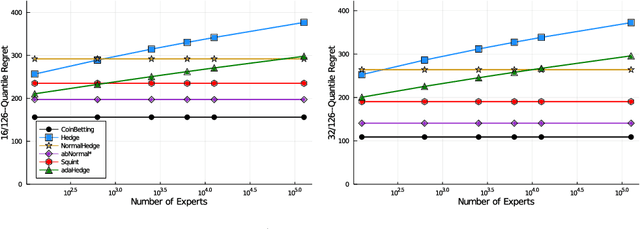
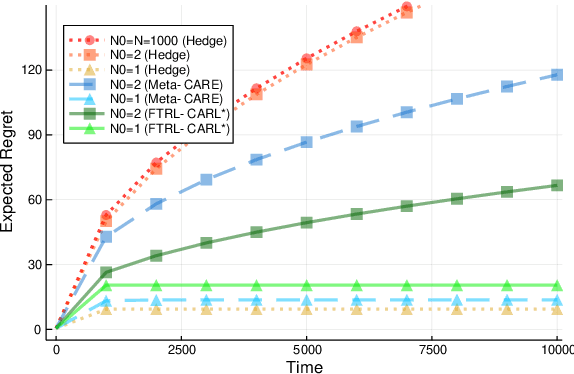
Quantile (and, more generally, KL) regret bounds, such as those achieved by NormalHedge (Chaudhuri, Freund, and Hsu 2009) and its variants, relax the goal of competing against the best individual expert to only competing against a majority of experts on adversarial data. More recently, the semi-adversarial paradigm (Bilodeau, Negrea, and Roy 2020) provides an alternative relaxation of adversarial online learning by considering data that may be neither fully adversarial nor stochastic (i.i.d.). We achieve the minimax optimal regret in both paradigms using FTRL with separate, novel, root-logarithmic regularizers, both of which can be interpreted as yielding variants of NormalHedge. We extend existing KL regret upper bounds, which hold uniformly over target distributions, to possibly uncountable expert classes with arbitrary priors; provide the first full-information lower bounds for quantile regret on finite expert classes (which are tight); and provide an adaptively minimax optimal algorithm for the semi-adversarial paradigm that adapts to the true, unknown constraint faster, leading to uniformly improved regret bounds over existing methods.

Relaxing the I.I.D. Assumption: Adaptive Minimax Optimal Sequential Prediction with Expert Advice

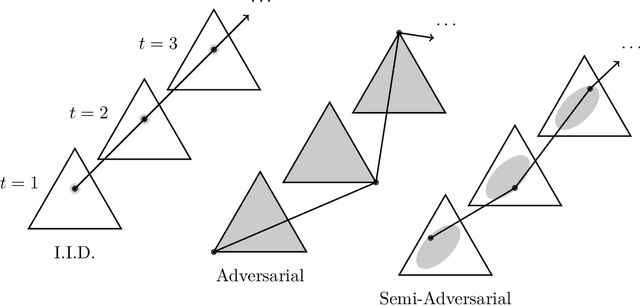
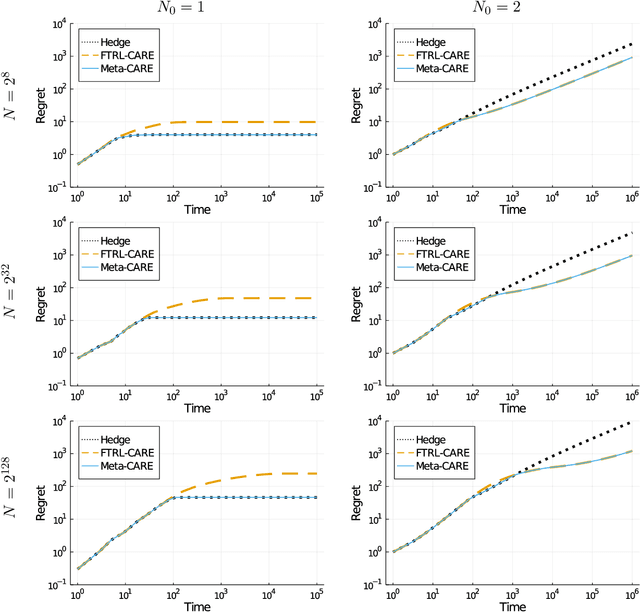
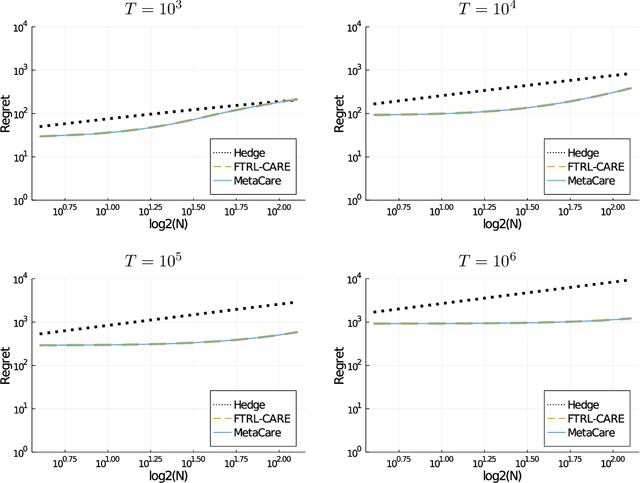
We consider sequential prediction with expert advice when the data are generated stochastically, but the distributions generating the data may vary arbitrarily among some constraint set. We quantify relaxations of the classical I.I.D. assumption in terms of possible constraint sets, with I.I.D. at one extreme, and an adversarial mechanism at the other. The Hedge algorithm, long known to be minimax optimal in the adversarial regime, has recently been shown to also be minimax optimal in the I.I.D. setting. We show that Hedge is suboptimal between these extremes, and present a new algorithm that is adaptively minimax optimal with respect to our relaxations of the I.I.D. assumption, without knowledge of which setting prevails.

Improved Bounds on Minimax Regret under Logarithmic Loss via Self-Concordance

We consider the classical problem of sequential probability assignment under logarithmic loss while competing against an arbitrary, potentially nonparametric class of experts. We obtain improved bounds on the minimax regret via a new approach that exploits the self-concordance property of the logarithmic loss. We show that for any expert class with (sequential) metric entropy $\mathcal{O}(\gamma^{-p})$ at scale $\gamma$, the minimax regret is $\mathcal{O}(n^{\frac{p}{p+1}})$, and that this rate cannot be improved without additional assumptions on the expert class under consideration. As an application of our techniques, we resolve the minimax regret for nonparametric Lipschitz classes of experts.