Relaxing the I.I.D. Assumption: Adaptive Minimax Optimal Sequential Prediction with Expert Advice

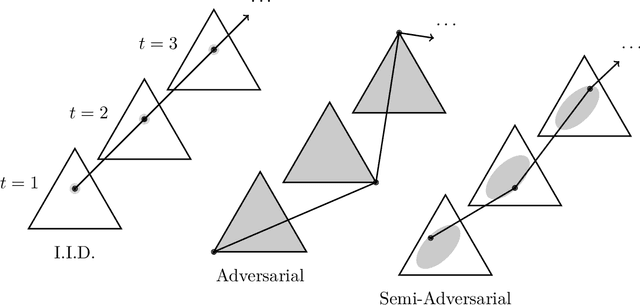
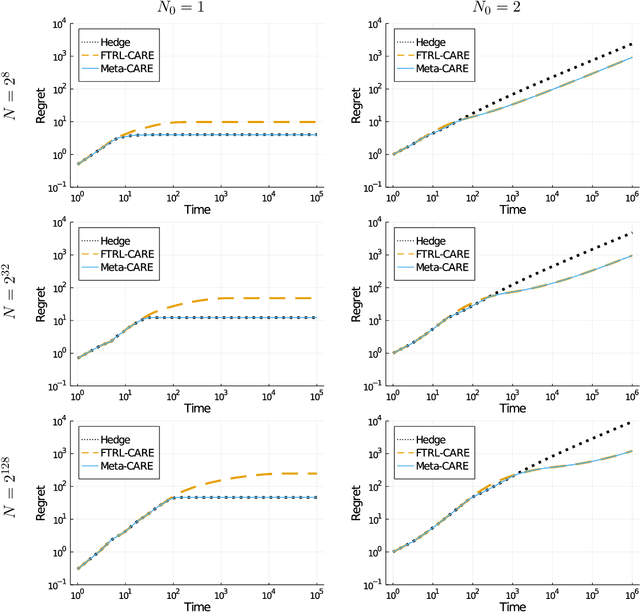
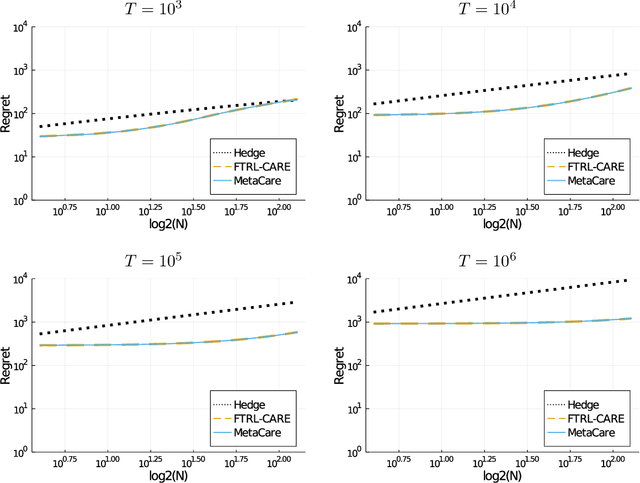
We consider sequential prediction with expert advice when the data are generated stochastically, but the distributions generating the data may vary arbitrarily among some constraint set. We quantify relaxations of the classical I.I.D. assumption in terms of possible constraint sets, with I.I.D. at one extreme, and an adversarial mechanism at the other. The Hedge algorithm, long known to be minimax optimal in the adversarial regime, has recently been shown to also be minimax optimal in the I.I.D. setting. We show that Hedge is suboptimal between these extremes, and present a new algorithm that is adaptively minimax optimal with respect to our relaxations of the I.I.D. assumption, without knowledge of which setting prevails.