Minimax Optimal Quantile and Semi-Adversarial Regret via Root-Logarithmic Regularizers

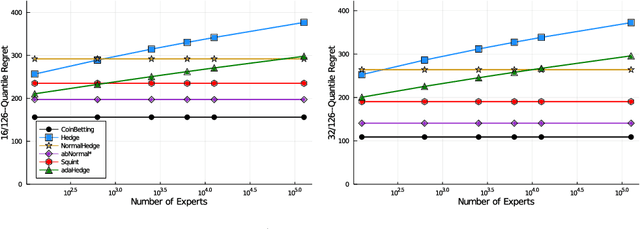
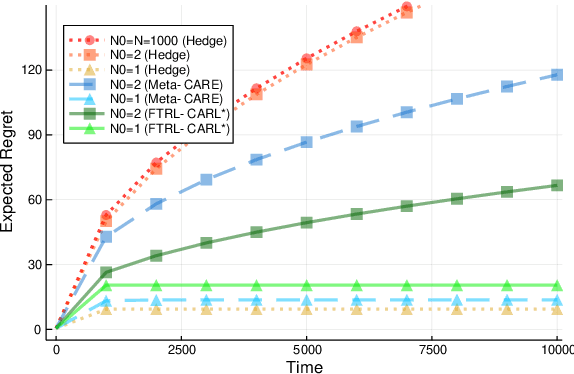
Quantile (and, more generally, KL) regret bounds, such as those achieved by NormalHedge (Chaudhuri, Freund, and Hsu 2009) and its variants, relax the goal of competing against the best individual expert to only competing against a majority of experts on adversarial data. More recently, the semi-adversarial paradigm (Bilodeau, Negrea, and Roy 2020) provides an alternative relaxation of adversarial online learning by considering data that may be neither fully adversarial nor stochastic (i.i.d.). We achieve the minimax optimal regret in both paradigms using FTRL with separate, novel, root-logarithmic regularizers, both of which can be interpreted as yielding variants of NormalHedge. We extend existing KL regret upper bounds, which hold uniformly over target distributions, to possibly uncountable expert classes with arbitrary priors; provide the first full-information lower bounds for quantile regret on finite expert classes (which are tight); and provide an adaptively minimax optimal algorithm for the semi-adversarial paradigm that adapts to the true, unknown constraint faster, leading to uniformly improved regret bounds over existing methods.

A closer look at temporal variability in dynamic online learning

This work focuses on the setting of dynamic regret in the context of online learning with full information. In particular, we analyze regret bounds with respect to the temporal variability of the loss functions. By assuming that the sequence of loss functions does not vary much with time, we show that it is possible to incur improved regret bounds compared to existing results. The key to our approach is to use the loss function (and not its gradient) during the optimization process. Building on recent advances in the analysis of Implicit algorithms, we propose an adaptation of the Implicit version of Online Mirror Descent to the dynamic setting. Our proposed algorithm is adaptive not only to the temporal variability of the loss functions, but also to the path length of the sequence of comparators when an upper bound is known. Furthermore, our analysis reveals that our results are tight and cannot be improved without further assumptions. Next, we show how our algorithm can be applied to the setting of learning with expert advice or to settings with composite loss functions. Finally, when an upper bound to the path-length is not fixed beforehand we show how to combine a greedy strategy with existing strongly-adaptive algorithms to compete optimally against different sequences of comparators simultaneously.

Temporal Variability in Implicit Online Learning

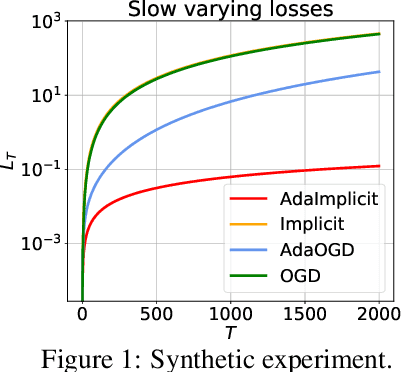
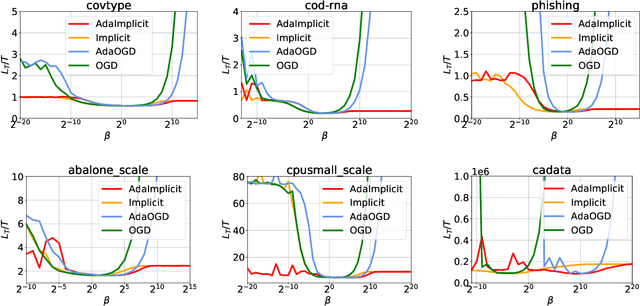
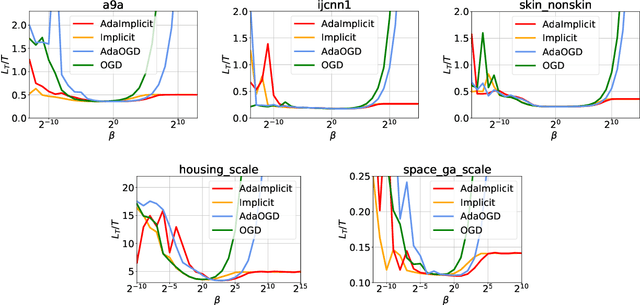
In the setting of online learning, Implicit algorithms turn out to be highly successful from a practical standpoint. However, the tightest regret analyses only show marginal improvements over Online Mirror Descent. In this work, we shed light on this behavior carrying out a careful regret analysis. We prove a novel static regret bound that depends on the temporal variability of the sequence of loss functions, a quantity which is often encountered when considering dynamic competitors. We show, for example, that the regret can be constant if the temporal variability is constant and the learning rate is tuned appropriately, without the need of smooth losses. Moreover, we present an adaptive algorithm that achieves this regret bound without prior knowledge of the temporal variability and prove a matching lower bound. Finally, we validate our theoretical findings on classification and regression datasets.