Region Feature Descriptor Adapted to High Affine Transformations

To address the issue of feature descriptors being ineffective in representing grayscale feature information when images undergo high affine transformations, leading to a rapid decline in feature matching accuracy, this paper proposes a region feature descriptor based on simulating affine transformations using classification. The proposed method initially categorizes images with different affine degrees to simulate affine transformations and generate a new set of images. Subsequently, it calculates neighborhood information for feature points on this new image set. Finally, the descriptor is generated by combining the grayscale histogram of the maximum stable extremal region to which the feature point belongs and the normalized position relative to the grayscale centroid of the feature point's region. Experimental results, comparing feature matching metrics under affine transformation scenarios, demonstrate that the proposed descriptor exhibits higher precision and robustness compared to existing classical descriptors. Additionally, it shows robustness when integrated with other descriptors.

A Robust Error-Resistant View Selection Method for 3D Reconstruction

To address the issue of increased triangulation uncertainty caused by selecting views with small camera baselines in Structure from Motion (SFM) view selection, this paper proposes a robust error-resistant view selection method. The method utilizes a triangulation-based computation to obtain an error-resistant model, which is then used to construct an error-resistant matrix. The sorting results of each row in the error-resistant matrix determine the candidate view set for each view. By traversing the candidate view sets of all views and completing the missing views based on the error-resistant matrix, the integrity of 3D reconstruction is ensured. Experimental comparisons between this method and the exhaustive method with the highest accuracy in the COLMAP program are conducted in terms of average reprojection error and absolute trajectory error in the reconstruction results. The proposed method demonstrates an average reduction of 29.40% in reprojection error accuracy and 5.07% in absolute trajectory error on the TUM dataset and DTU dataset.

Conditional Distribution Function Estimation Using Neural Networks for Censored and Uncensored Data

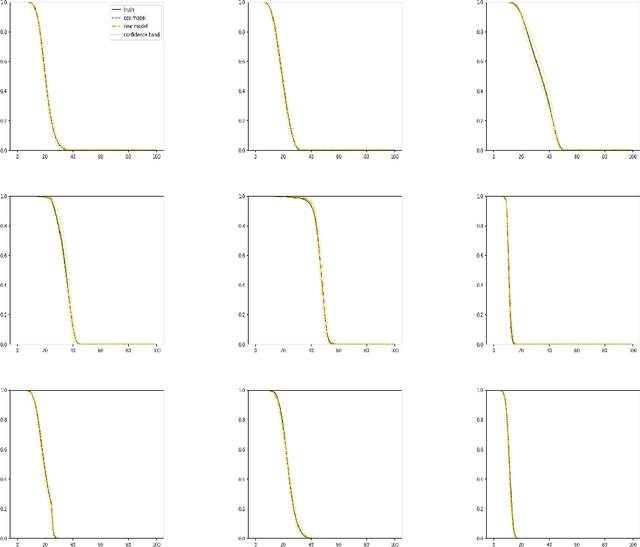
Most work in neural networks focuses on estimating the conditional mean of a continuous response variable given a set of covariates.In this article, we consider estimating the conditional distribution function using neural networks for both censored and uncensored data. The algorithm is built upon the data structure particularly constructed for the Cox regression with time-dependent covariates. Without imposing any model assumption, we consider a loss function that is based on the full likelihood where the conditional hazard function is the only unknown nonparametric parameter, for which unconstraint optimization methods can be applied. Through simulation studies, we show the proposed method possesses desirable performance, whereas the partial likelihood method and the traditional neural networks with $L_2$ loss yield biased estimates when model assumptions are violated. We further illustrate the proposed method with several real-world data sets. The implementation of the proposed methods is made available at https://github.com/bingqing0729/NNCDE.

Estimation of Large Covariance and Precision Matrices from Temporally Dependent Observations

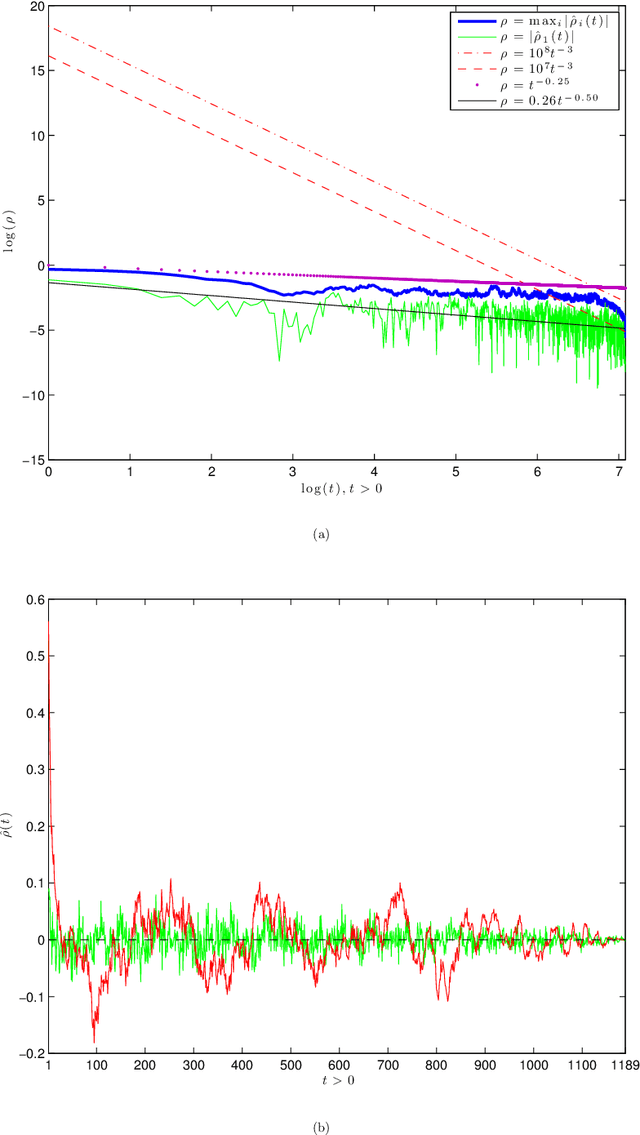
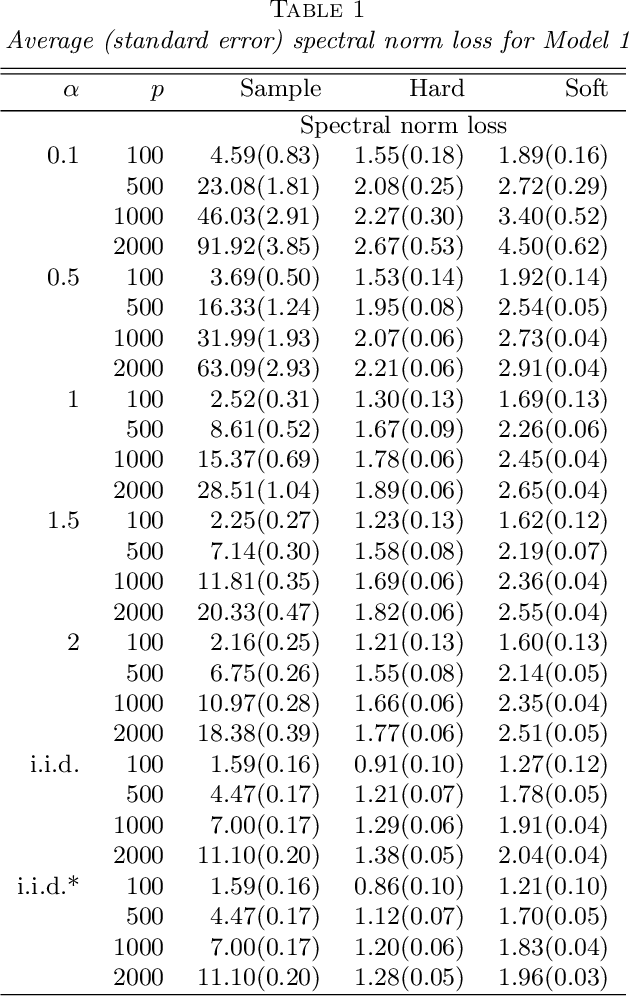
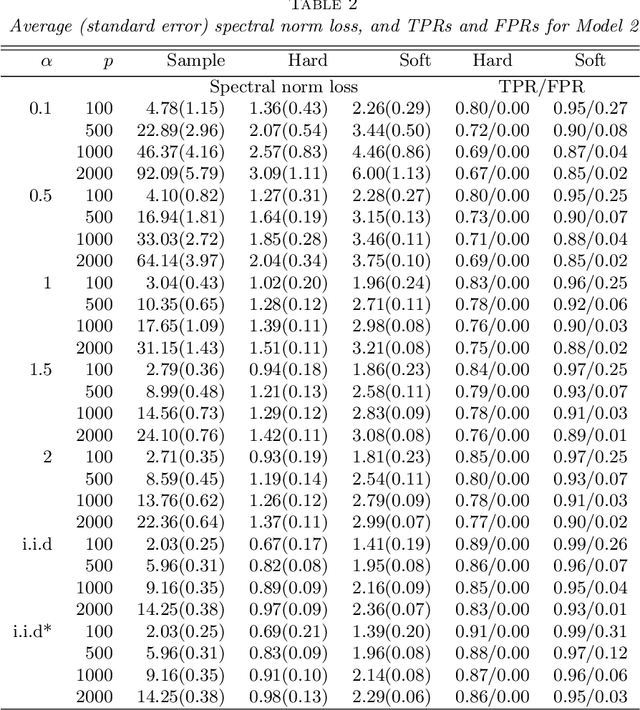
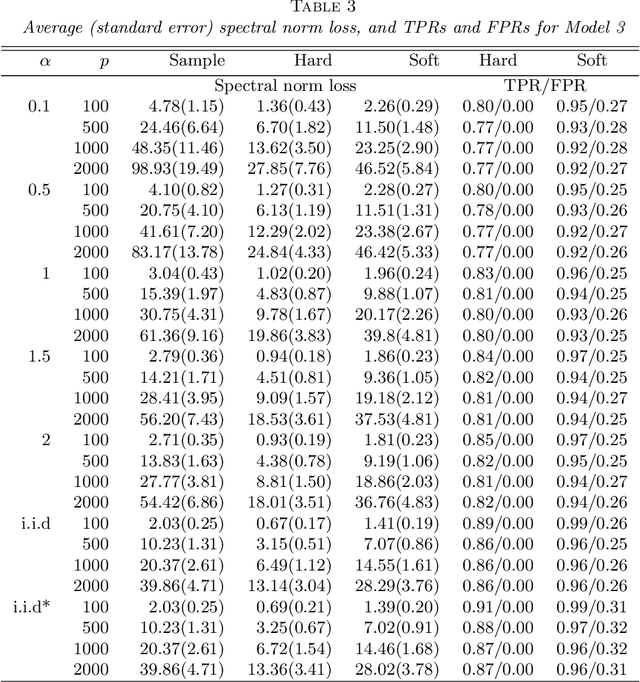
We consider the estimation of large covariance and precision matrices from high-dimensional sub-Gaussian or heavier-tailed observations with slowly decaying temporal dependence. The temporal dependence is allowed to be long-range so with longer memory than those considered in the current literature. We show that several commonly used methods for independent observations can be applied to the temporally dependent data. In particular, the rates of convergence are obtained for the generalized thresholding estimation of covariance and correlation matrices, and for the constrained $\ell_1$ minimization and the $\ell_1$ penalized likelihood estimation of precision matrix. Properties of sparsistency and sign-consistency are also established. A gap-block cross-validation method is proposed for the tuning parameter selection, which performs well in simulations. As a motivating example, we study the brain functional connectivity using resting-state fMRI time series data with long-range temporal dependence.

Multiple Testing for Neuroimaging via Hidden Markov Random Field

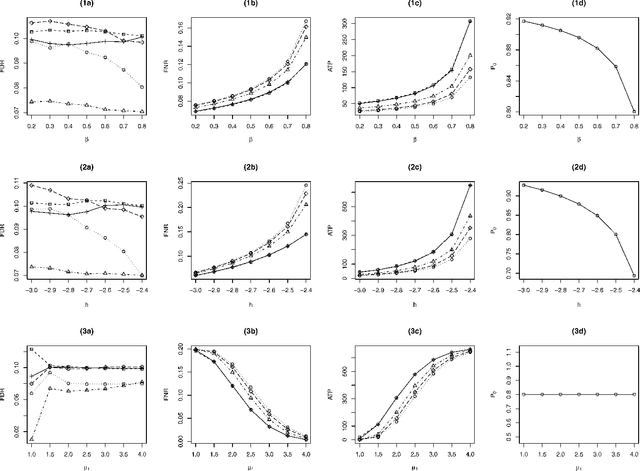
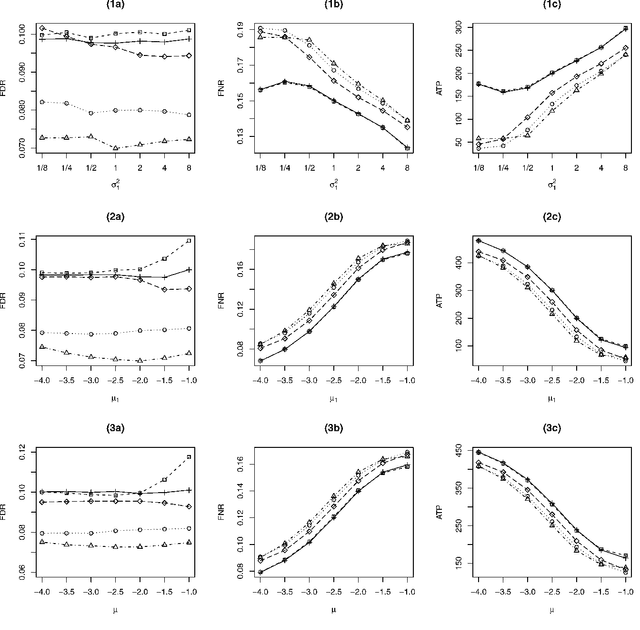
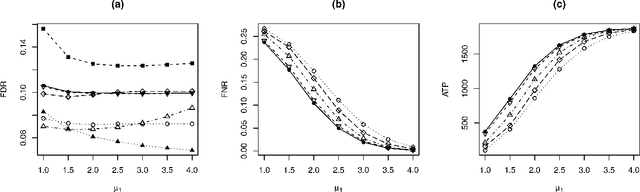
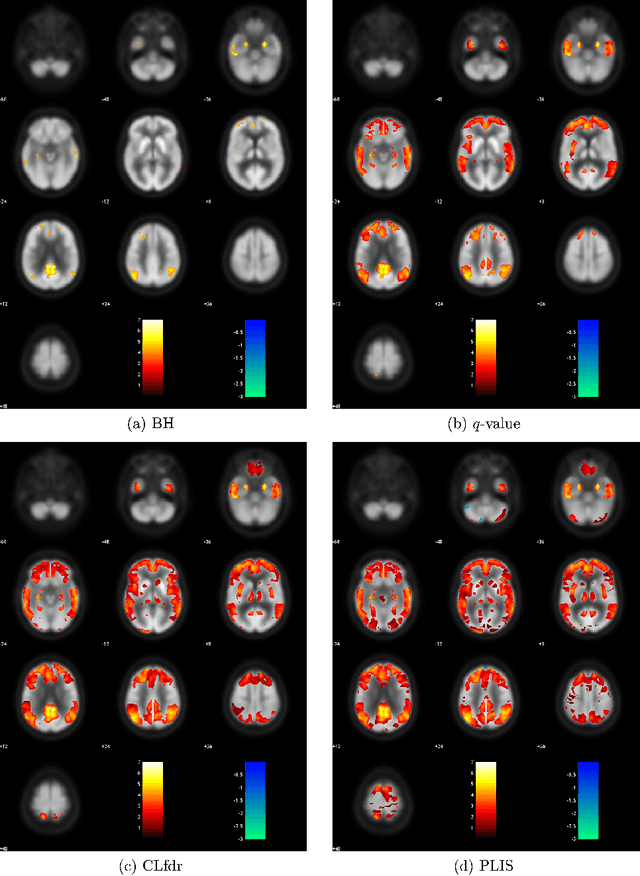
Traditional voxel-level multiple testing procedures in neuroimaging, mostly $p$-value based, often ignore the spatial correlations among neighboring voxels and thus suffer from substantial loss of power. We extend the local-significance-index based procedure originally developed for the hidden Markov chain models, which aims to minimize the false nondiscovery rate subject to a constraint on the false discovery rate, to three-dimensional neuroimaging data using a hidden Markov random field model. A generalized expectation-maximization algorithm for maximizing the penalized likelihood is proposed for estimating the model parameters. Extensive simulations show that the proposed approach is more powerful than conventional false discovery rate procedures. We apply the method to the comparison between mild cognitive impairment, a disease status with increased risk of developing Alzheimer's or another dementia, and normal controls in the FDG-PET imaging study of the Alzheimer's Disease Neuroimaging Initiative.

Non-asymptotic Oracle Inequalities for the High-Dimensional Cox Regression via Lasso

We consider the finite sample properties of the regularized high-dimensional Cox regression via lasso. Existing literature focuses on linear models or generalized linear models with Lipschitz loss functions, where the empirical risk functions are the summations of independent and identically distributed (iid) losses. The summands in the negative log partial likelihood function for censored survival data, however, are neither iid nor Lipschitz. We first approximate the negative log partial likelihood function by a sum of iid non-Lipschitz terms, then derive the non-asymptotic oracle inequalities for the lasso penalized Cox regression using pointwise arguments to tackle the difficulty caused by the lack of iid and Lipschitz property.