Generative Shape Models: Joint Text Recognition and Segmentation with Very Little Training Data

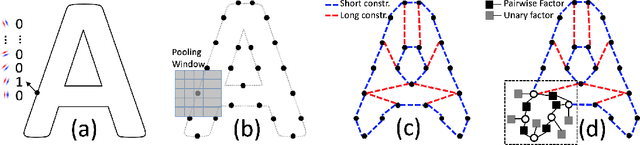
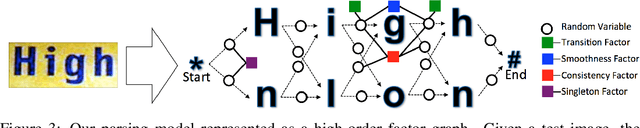
We demonstrate that a generative model for object shapes can achieve state of the art results on challenging scene text recognition tasks, and with orders of magnitude fewer training images than required for competing discriminative methods. In addition to transcribing text from challenging images, our method performs fine-grained instance segmentation of characters. We show that our model is more robust to both affine transformations and non-affine deformations compared to previous approaches.

Decayed MCMC Filtering

Filtering---estimating the state of a partially observable Markov process from a sequence of observations---is one of the most widely studied problems in control theory, AI, and computational statistics. Exact computation of the posterior distribution is generally intractable for large discrete systems and for nonlinear continuous systems, so a good deal of effort has gone into developing robust approximation algorithms. This paper describes a simple stochastic approximation algorithm for filtering called {em decayed MCMC}. The algorithm applies Markov chain Monte Carlo sampling to the space of state trajectories using a proposal distribution that favours flips of more recent state variables. The formal analysis of the algorithm involves a generalization of standard coupling arguments for MCMC convergence. We prove that for any ergodic underlying Markov process, the convergence time of decayed MCMC with inverse-polynomial decay remains bounded as the length of the observation sequence grows. We show experimentally that decayed MCMC is at least competitive with other approximation algorithms such as particle filtering.

A compact, hierarchical Q-function decomposition

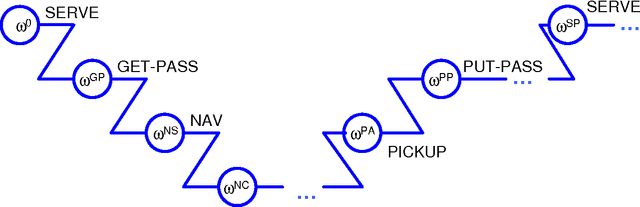
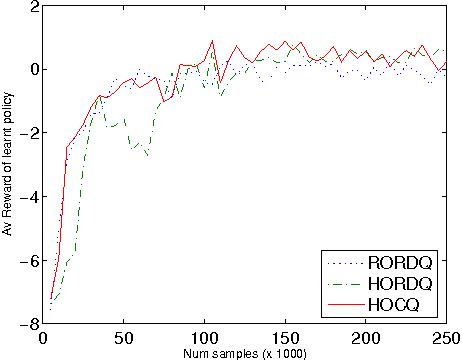
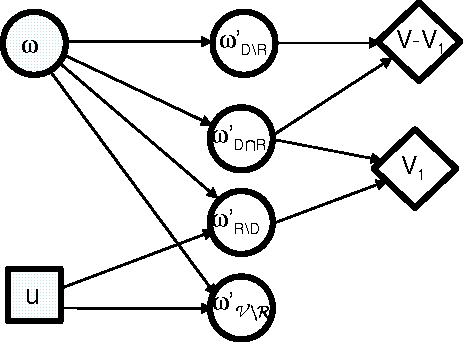
Previous work in hierarchical reinforcement learning has faced a dilemma: either ignore the values of different possible exit states from a subroutine, thereby risking suboptimal behavior, or represent those values explicitly thereby incurring a possibly large representation cost because exit values refer to nonlocal aspects of the world (i.e., all subsequent rewards). This paper shows that, in many cases, one can avoid both of these problems. The solution is based on recursively decomposing the exit value function in terms of Q-functions at higher levels of the hierarchy. This leads to an intuitively appealing runtime architecture in which a parent subroutine passes to its child a value function on the exit states and the child reasons about how its choices affect the exit value. We also identify structural conditions on the value function and transition distributions that allow much more concise representations of exit state distributions, leading to further state abstraction. In essence, the only variables whose exit values need be considered are those that the parent cares about and the child affects. We demonstrate the utility of our algorithms on a series of increasingly complex environments.