A compact, hierarchical Q-function decomposition
Paper and Code
Jun 27, 2012
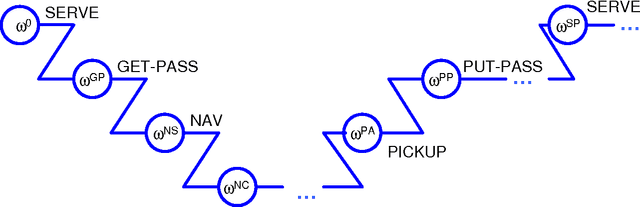
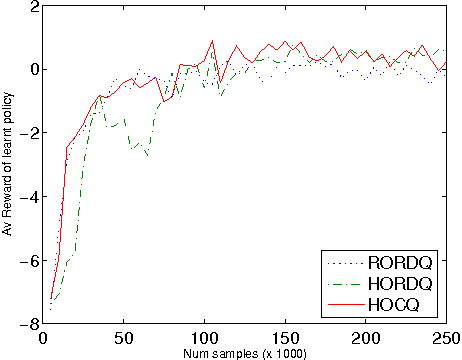
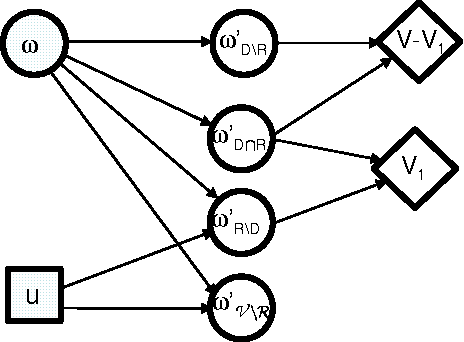
Previous work in hierarchical reinforcement learning has faced a dilemma: either ignore the values of different possible exit states from a subroutine, thereby risking suboptimal behavior, or represent those values explicitly thereby incurring a possibly large representation cost because exit values refer to nonlocal aspects of the world (i.e., all subsequent rewards). This paper shows that, in many cases, one can avoid both of these problems. The solution is based on recursively decomposing the exit value function in terms of Q-functions at higher levels of the hierarchy. This leads to an intuitively appealing runtime architecture in which a parent subroutine passes to its child a value function on the exit states and the child reasons about how its choices affect the exit value. We also identify structural conditions on the value function and transition distributions that allow much more concise representations of exit state distributions, leading to further state abstraction. In essence, the only variables whose exit values need be considered are those that the parent cares about and the child affects. We demonstrate the utility of our algorithms on a series of increasingly complex environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge