Certified Grasping

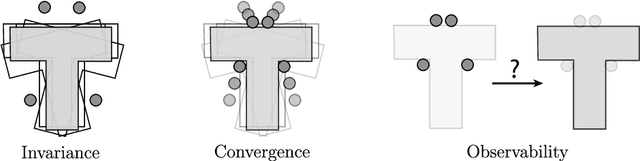
This paper studies robustness in planar grasping from a geometric perspective. By treating grasping as a process that shapes the free-space of an object over time, we can define three types of certificates to guarantee success of a grasp: (a) invariance under an initial set, (b) convergence towards a goal grasp, and (c) observability over the final object pose. We develop convex-combinatorial models for each of these certificates, which can be expressed as simple semi-algebraic relations under mild-modeling assumptions. By leveraging these models to synthesize certificates, we optimize certifiable grasps of arbitrary planar objects composed as a union of convex polygons, using manipulators described as point-fingers. We validate this approach with simulations and real robot experiments, by grasping random polygons, comparing against other standard grasp planning algorithms, and performing sensorless grasps over different objects.

Simultaneous Contact, Gait and Motion Planning for Robust Multi-Legged Locomotion via Mixed-Integer Convex Optimization

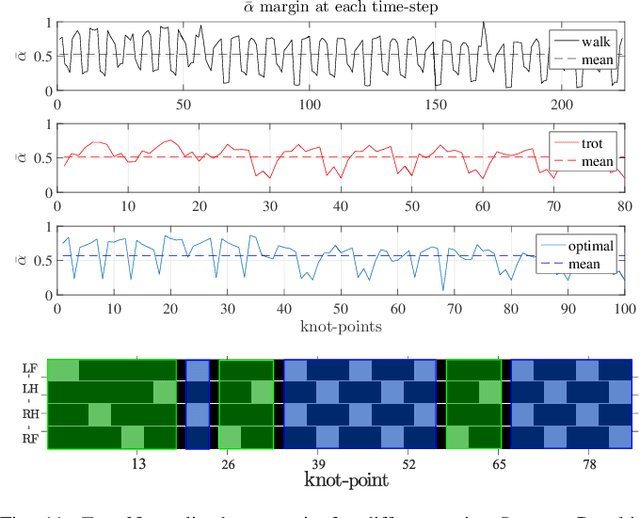
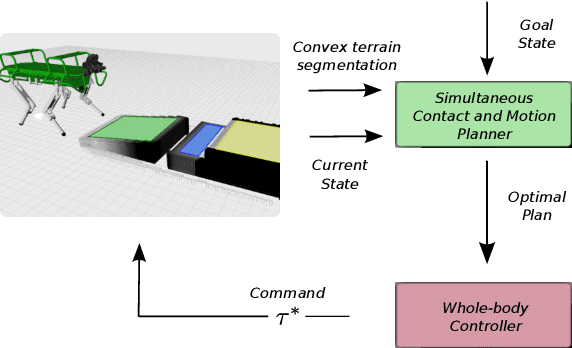
Traditional motion planning approaches for multi-legged locomotion divide the problem into several stages, such as contact search and trajectory generation. However, reasoning about contacts and motions simultaneously is crucial for the generation of complex whole-body behaviors. Currently, coupling theses problems has required either the assumption of a fixed gait sequence and flat terrain condition, or non-convex optimization with intractable computation time. In this paper, we propose a mixed-integer convex formulation to plan simultaneously contact locations, gait transitions and motion, in a computationally efficient fashion. In contrast to previous works, our approach is not limited to flat terrain nor to a pre-specified gait sequence. Instead, we incorporate the friction cone stability margin, approximate the robot's torque limits, and plan the gait using mixed-integer convex constraints. We experimentally validated our approach on the HyQ robot by traversing different challenging terrains, where non-convexity and flat terrain assumptions might lead to sub-optimal or unstable plans. Our method increases the motion generality while keeping a low computation time.

A Convex-Combinatorial Model for Planar Caging

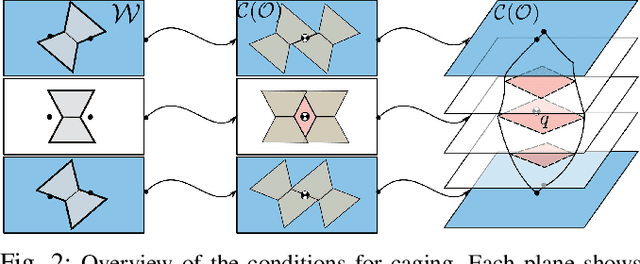
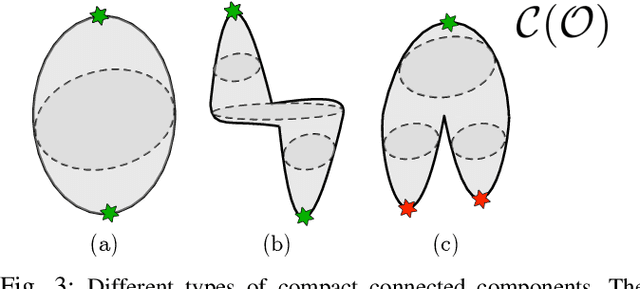
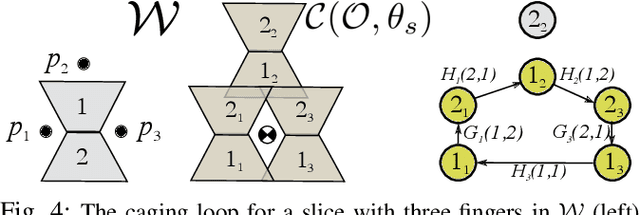
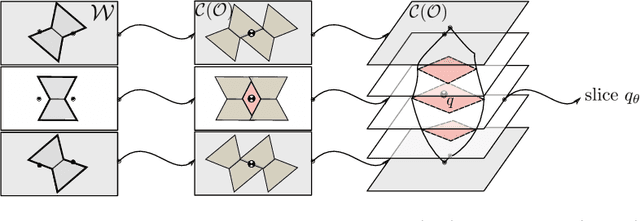
Caging is a promising tool which allows a robot to manipulate an object without directly reasoning about the contact dynamics involved. Furthermore, caging also provides useful guarantees in terms of robustness to uncertainty, and often serves as a way-point to a grasp. Unfortunately, previous work on caging is often based on computational geometry or discrete topology tools, causing restriction on gripper geometry, and difficulty on integration into larger manipulation frameworks. In this paper, we develop a convex-combinatorial model to characterize caging from an optimization perspective. More specifically, we study the configuration space of the object, where the fingers act as obstacles that enclose the configuration of the object. The convex-combinatorial nature of this approach provides guarantees on optimality, convergence and scalability, and its optimization nature makes it adaptable for further applications on robot manipulation tasks.

A Generalized Mixed-Integer Convex Program for Multilegged Footstep Planning on Uneven Terrain

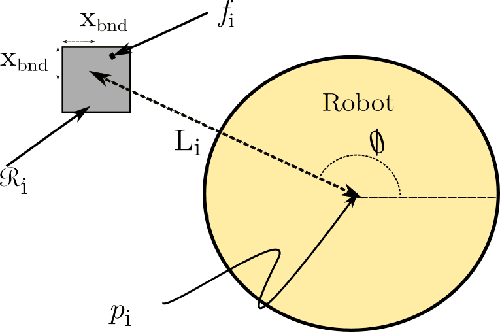
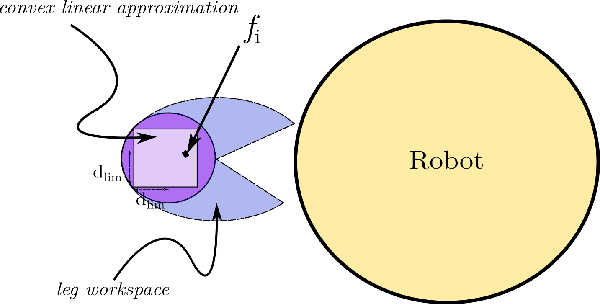
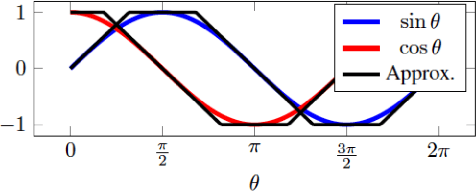
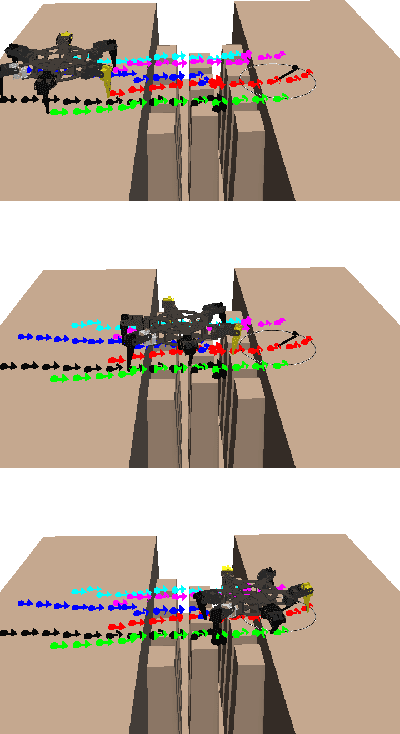
Robot footstep planning strategies can be divided in two main approaches: discrete searches and continuous optimizations. While discrete searches have been broadly applied, continuous optimizations approaches have been restricted for humanoid platforms. This article introduces a generalized continuous-optimization approach for multilegged footstep planning which can be adapted to different platforms, regardless the number and geometry of legs. This approach leverages Mixed-Integer Convex Programming to account for the non-convex constraints that represent footstep rotation and obstacle avoidance. The planning problem is formulated as an optimization problem which considers robot geometry and reachability with linear constraints, and can be efficiently solved using optimization software. To demonstrate the functionality and adaptability of the planner, a set of tests are performed on a BH3R hexapod and a LittleDog quadruped on scenarios which can't be easily handled with discrete searches, such tests are solved efficiently in fractions of a second. This work represents, to the knowledge of the authors, the first successful implementation of a continuous optimization-based multilegged footstep planner.