Certified Grasping
Paper and Code
Sep 09, 2019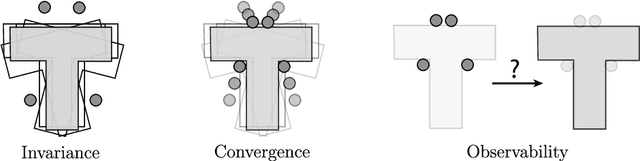
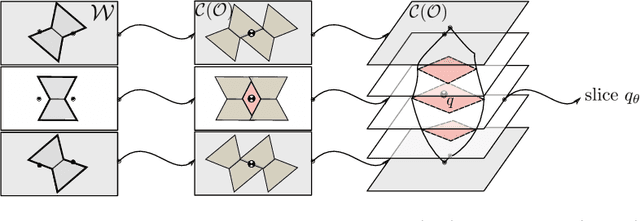


This paper studies robustness in planar grasping from a geometric perspective. By treating grasping as a process that shapes the free-space of an object over time, we can define three types of certificates to guarantee success of a grasp: (a) invariance under an initial set, (b) convergence towards a goal grasp, and (c) observability over the final object pose. We develop convex-combinatorial models for each of these certificates, which can be expressed as simple semi-algebraic relations under mild-modeling assumptions. By leveraging these models to synthesize certificates, we optimize certifiable grasps of arbitrary planar objects composed as a union of convex polygons, using manipulators described as point-fingers. We validate this approach with simulations and real robot experiments, by grasping random polygons, comparing against other standard grasp planning algorithms, and performing sensorless grasps over different objects.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge