Manifold-aware Synthesis of High-resolution Diffusion from Structural Imaging

The physical and clinical constraints surrounding diffusion-weighted imaging (DWI) often limit the spatial resolution of the produced images to voxels up to 8 times larger than those of T1w images. Thus, the detailed information contained in T1w imagescould help in the synthesis of diffusion images in higher resolution. However, the non-Euclidean nature of diffusion imaging hinders current deep generative models from synthesizing physically plausible images. In this work, we propose the first Riemannian network architecture for the direct generation of diffusion tensors (DT) and diffusion orientation distribution functions (dODFs) from high-resolution T1w images. Our integration of the Log-Euclidean Metric into a learning objective guarantees, unlike standard Euclidean networks, the mathematically-valid synthesis of diffusion. Furthermore, our approach improves the fractional anisotropy mean squared error (FA MSE) between the synthesized diffusion and the ground-truth by more than 23% and the cosine similarity between principal directions by almost 5% when compared to our baselines. We validate our generated diffusion by comparing the resulting tractograms to our expected real data. We observe similar fiber bundles with streamlines having less than 3% difference in length, less than 1% difference in volume, and a visually close shape. While our method is able to generate high-resolution diffusion images from structural inputs in less than 15 seconds, we acknowledge and discuss the limits of diffusion inference solely relying on T1w images. Our results nonetheless suggest a relationship between the high-level geometry of the brain and the overall white matter architecture.

Manifold-Aware Synthesis of High Resolution Diffusion from Structural Imaging

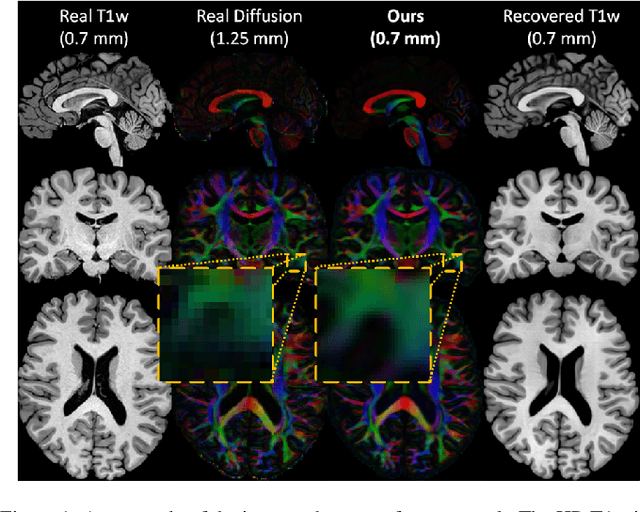
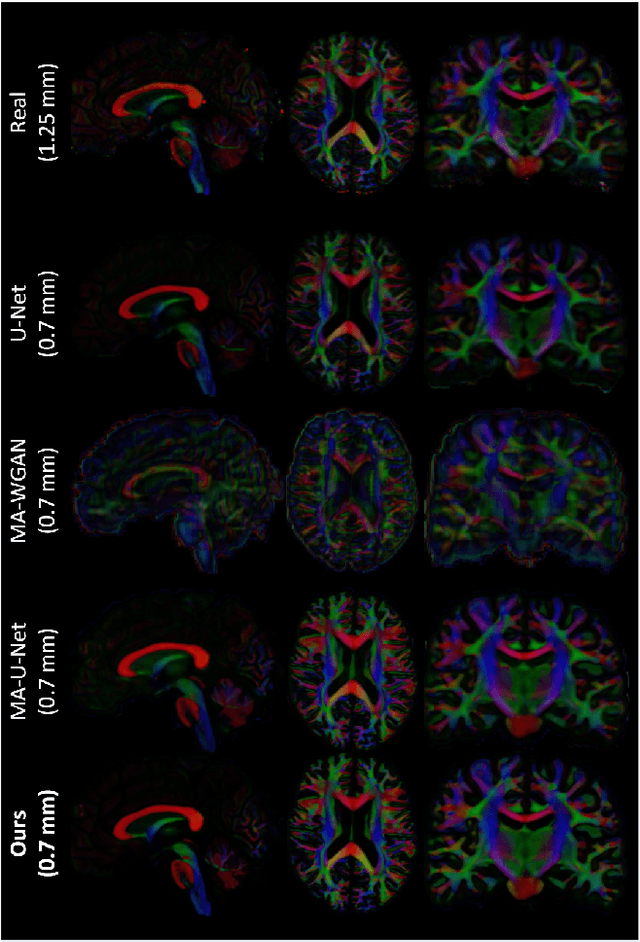
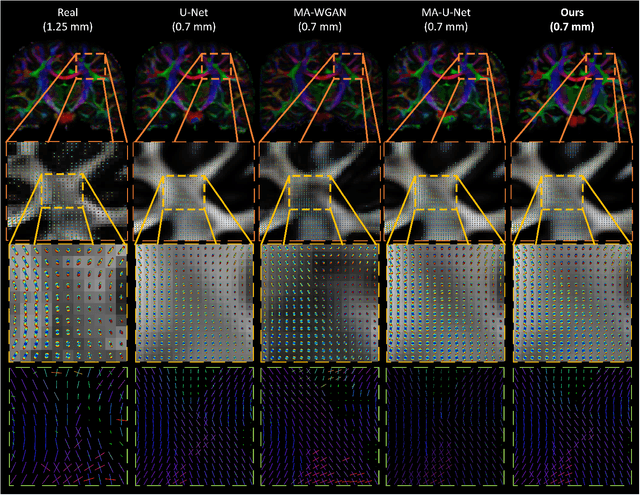
The physical and clinical constraints surrounding diffusion-weighted imaging (DWI) often limit the spatial resolution of the produced images to voxels up to 8 times larger than those of T1w images. Thus, the detailed information contained in T1w imagescould help in the synthesis of diffusion images in higher resolution. However, the non-Euclidean nature of diffusion imaging hinders current deep generative models from synthesizing physically plausible images. In this work, we propose the first Riemannian network architecture for the direct generation of diffusion tensors (DT) and diffusion orientation distribution functions (dODFs) from high-resolution T1w images. Our integration of the Log-Euclidean Metric into a learning objective guarantees, unlike standard Euclidean networks, the mathematically-valid synthesis of diffusion. Furthermore, our approach improves the fractional anisotropy mean squared error (FA MSE) between the synthesized diffusion and the ground-truth by more than 23% and the cosine similarity between principal directions by almost 5% when compared to our baselines. We validate our generated diffusion by comparing the resulting tractograms to our expected real data. We observe similar fiber bundles with streamlines having less than 3% difference in length, less than 1% difference in volume, and a visually close shape. While our method is able to generate high-resolution diffusion images from structural inputs in less than 15 seconds, we acknowledge and discuss the limits of diffusion inference solely relying on T1w images. Our results nonetheless suggest a relationship between the high-level geometry of the brain and the overall white matter architecture.

Realistic Image Normalization for Multi-Domain Segmentation

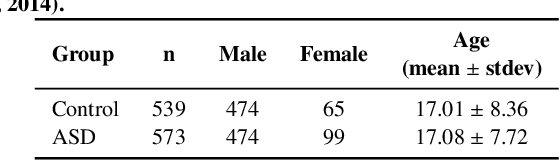
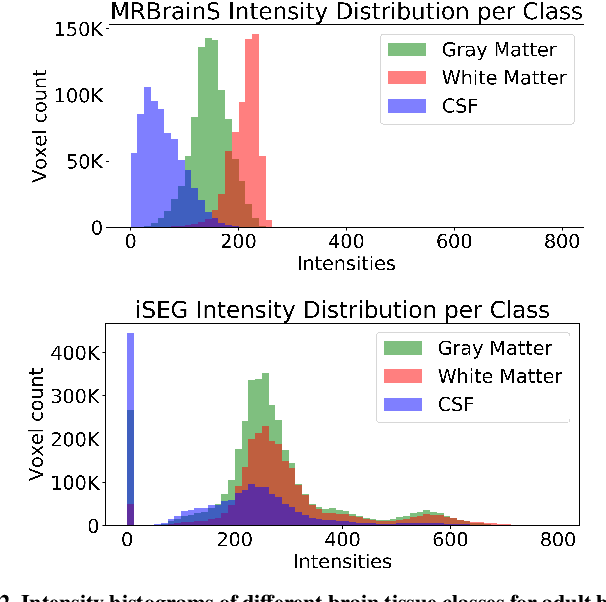
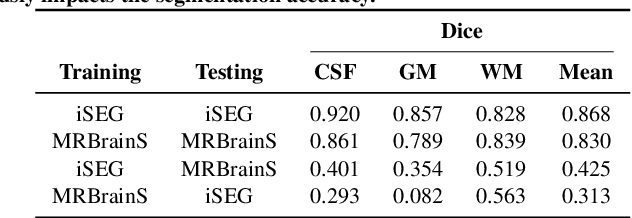
Image normalization is a building block in medical image analysis. Conventional approaches are customarily utilized on a per-dataset basis. This strategy, however, prevents the current normalization algorithms from fully exploiting the complex joint information available across multiple datasets. Consequently, ignoring such joint information has a direct impact on the performance of segmentation algorithms. This paper proposes to revisit the conventional image normalization approach by instead learning a common normalizing function across multiple datasets. Jointly normalizing multiple datasets is shown to yield consistent normalized images as well as an improved image segmentation. To do so, a fully automated adversarial and task-driven normalization approach is employed as it facilitates the training of realistic and interpretable images while keeping performance on-par with the state-of-the-art. The adversarial training of our network aims at finding the optimal transfer function to improve both the segmentation accuracy and the generation of realistic images. We evaluated the performance of our normalizer on both infant and adult brains images from the iSEG, MRBrainS and ABIDE datasets. Results reveal the potential of our normalization approach for segmentation, with Dice improvements of up to 57.5% over our baseline. Our method can also enhance data availability by increasing the number of samples available when learning from multiple imaging domains.

Manifold-Aware CycleGAN for High Resolution Structural-to-DTI Synthesis

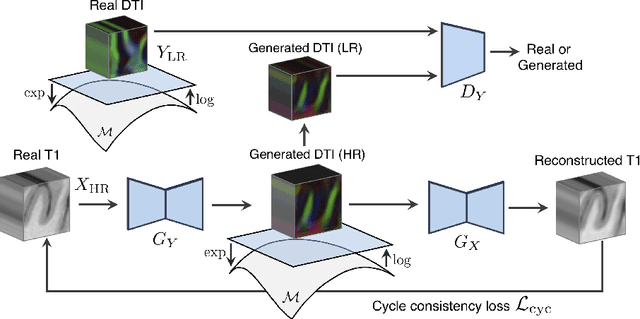
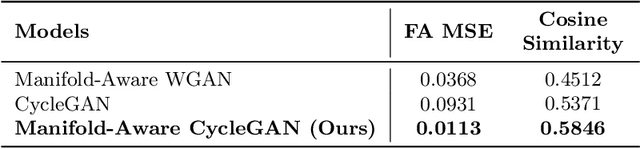
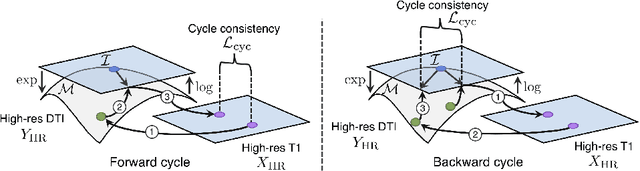
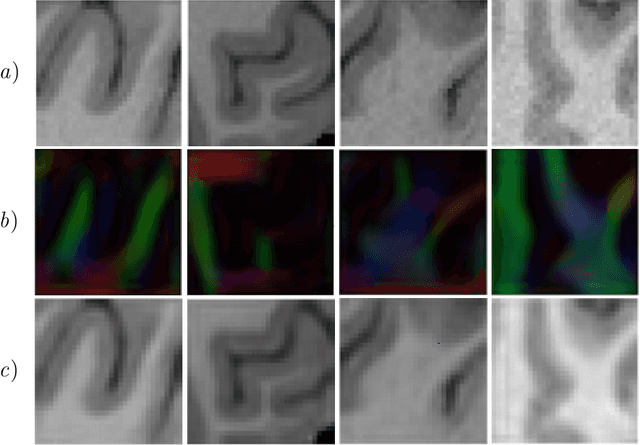
Unpaired image-to-image translation has been applied successfully to natural images but has received very little attention for manifold-valued data such as in diffusion tensor imaging (DTI). The non-Euclidean nature of DTI prevents current generative adversarial networks (GANs) from generating plausible images and has mostly limited their application to diffusion MRI scalar maps, such as fractional anisotropy (FA) or mean diffusivity (MD). Even if these scalar maps are clinically useful, they mostly ignore fiber orientations and have, therefore, limited applications for analyzing brain fibers, for instance, impairing fiber tractography. Here, we propose a manifold-aware CycleGAN that learns the generation of high resolution DTI from unpaired T1w images. We formulate the objective as a Wasserstein distance minimization problem of data distributions on a Riemannian manifold of symmetric positive definite 3x3 matrices SPD(3), using adversarial and cycle-consistency losses. To ensure that the generated diffusion tensors lie on the SPD(3) manifold, we exploit the theoretical properties of the exponential and logarithm maps. We demonstrate that, unlike standard GANs, our method is able to generate realistic high resolution DTI that can be used to compute diffusion-based metrics and run fiber tractography algorithms. To evaluate our model's performance, we compute the cosine similarity between the generated tensors principal orientation and their ground truth orientation and the mean squared error (MSE) of their derived FA values. We demonstrate that our method produces up to 8 times better FA MSE than a standard CycleGAN and 30% better cosine similarity than a manifold-aware Wasserstein GAN while synthesizing sharp high resolution DTI.

Adversarial normalization for multi domain image segmentation

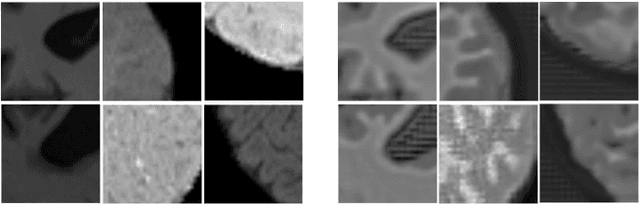
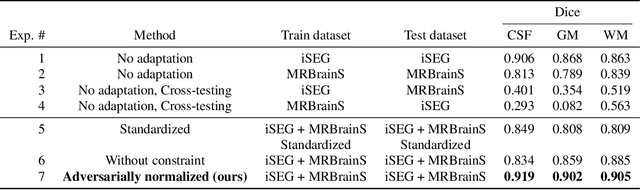
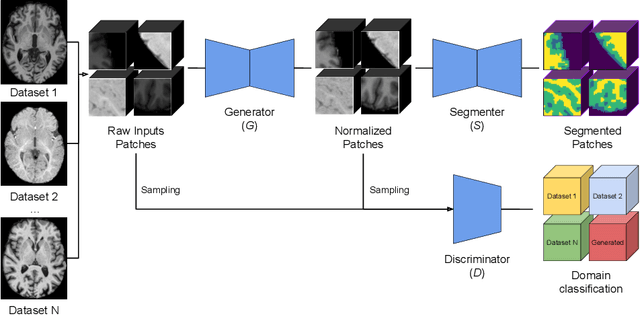
Image normalization is a critical step in medical imaging. This step is often done on a per-dataset basis, preventing current segmentation algorithms from the full potential of exploiting jointly normalized information across multiple datasets. To solve this problem, we propose an adversarial normalization approach for image segmentation which learns common normalizing functions across multiple datasets while retaining image realism. The adversarial training provides an optimal normalizer that improves both the segmentation accuracy and the discrimination of unrealistic normalizing functions. Our contribution therefore leverages common imaging information from multiple domains. The optimality of our common normalizer is evaluated by combining brain images from both infants and adults. Results on the challenging iSEG and MRBrainS datasets reveal the potential of our adversarial normalization approach for segmentation, with Dice improvements of up to 59.6% over the baseline.