Manifold-Aware CycleGAN for High Resolution Structural-to-DTI Synthesis

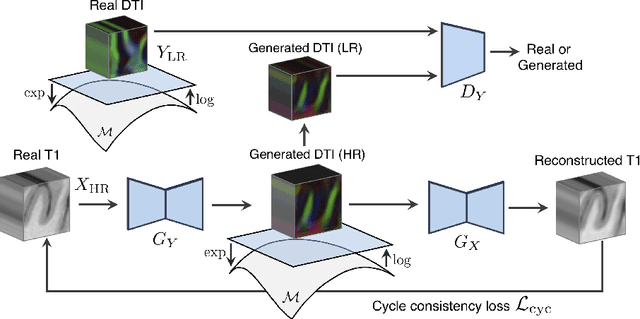
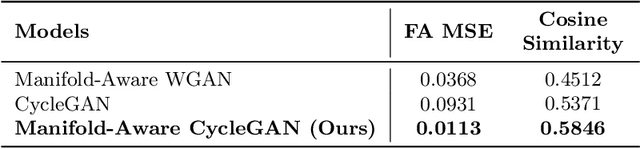
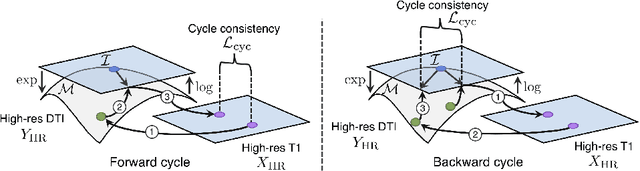
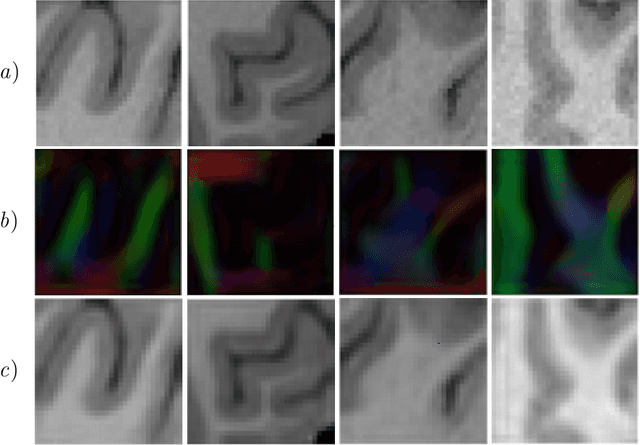
Unpaired image-to-image translation has been applied successfully to natural images but has received very little attention for manifold-valued data such as in diffusion tensor imaging (DTI). The non-Euclidean nature of DTI prevents current generative adversarial networks (GANs) from generating plausible images and has mostly limited their application to diffusion MRI scalar maps, such as fractional anisotropy (FA) or mean diffusivity (MD). Even if these scalar maps are clinically useful, they mostly ignore fiber orientations and have, therefore, limited applications for analyzing brain fibers, for instance, impairing fiber tractography. Here, we propose a manifold-aware CycleGAN that learns the generation of high resolution DTI from unpaired T1w images. We formulate the objective as a Wasserstein distance minimization problem of data distributions on a Riemannian manifold of symmetric positive definite 3x3 matrices SPD(3), using adversarial and cycle-consistency losses. To ensure that the generated diffusion tensors lie on the SPD(3) manifold, we exploit the theoretical properties of the exponential and logarithm maps. We demonstrate that, unlike standard GANs, our method is able to generate realistic high resolution DTI that can be used to compute diffusion-based metrics and run fiber tractography algorithms. To evaluate our model's performance, we compute the cosine similarity between the generated tensors principal orientation and their ground truth orientation and the mean squared error (MSE) of their derived FA values. We demonstrate that our method produces up to 8 times better FA MSE than a standard CycleGAN and 30% better cosine similarity than a manifold-aware Wasserstein GAN while synthesizing sharp high resolution DTI.