Separable Dictionary Learning with Global Optimality and Applications to Diffusion MRI

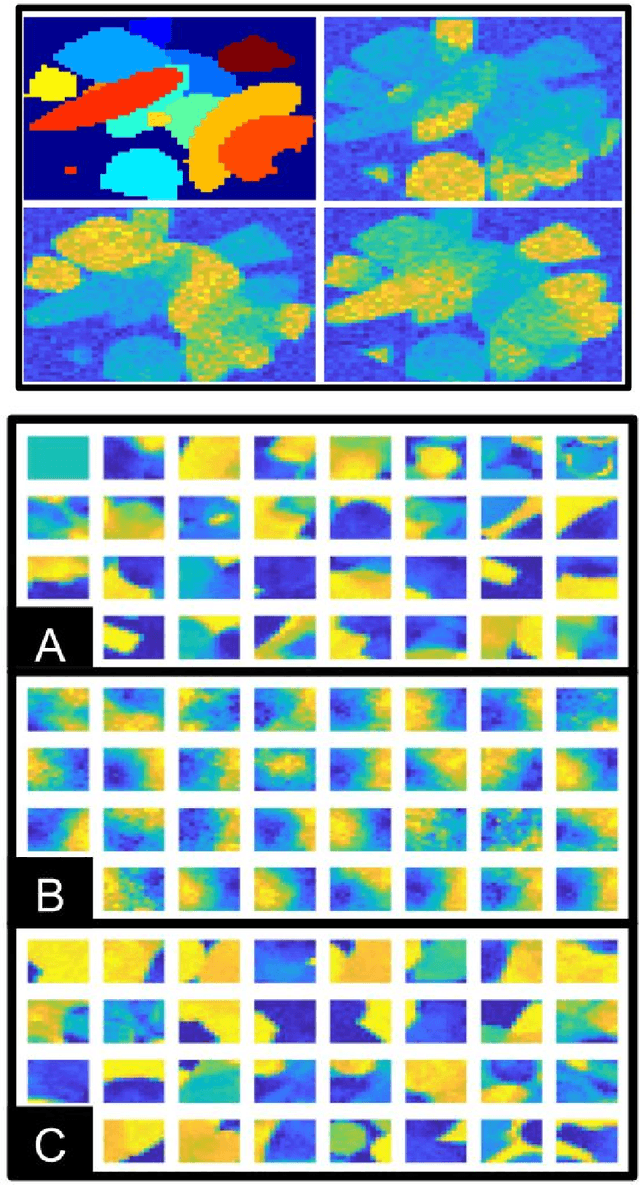
Dictionary learning is a popular class of methods for modeling complex data by learning sparse representations directly from the data. For some large-scale applications, exploiting a known structure of the signal is often essential for reducing the complexity of algorithms and representations. One such method is tensor factorization by which a large multi-dimensional dataset can be explicitly factored or separated along each dimension of the data in order to break the representation up into smaller components. Learning dictionaries for tensor structured data is called tensor or separable dictionary learning. While there have been many recent works on separable dictionary learning, typical formulations involve solving a non-convex optimization problem and guaranteeing global optimality remains a challenge. In this work, we propose a framework that uses recent developments in matrix/tensor factorization to provide theoretical and numerical guarantees of the global optimality for the separable dictionary learning problem. We will demonstrate our algorithm on diffusion magnetic resonance imaging (dMRI) data, a medical imaging modality which measures water diffusion along multiple angular directions in every voxel of an MRI volume. For this application, state-of-the-art methods learn dictionaries for the angular domain of the signals without consideration for the spatial domain. In this work, we apply the proposed separable dictionary learning method to learn spatial and angular dMRI dictionaries jointly and show results on denoising phantom and real dMRI brain data.

Dropout as a Low-Rank Regularizer for Matrix Factorization

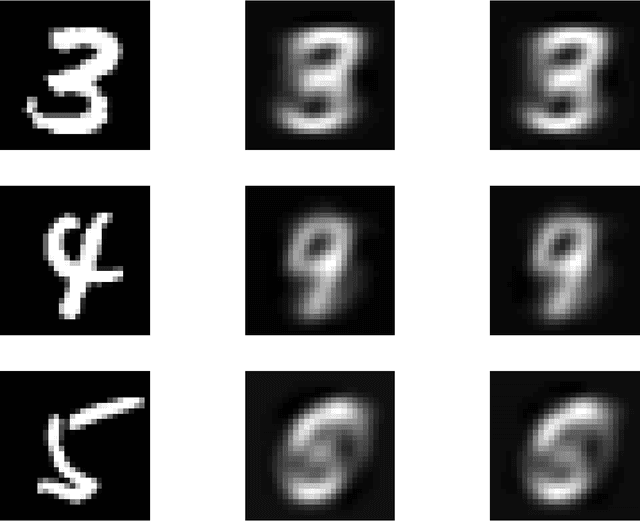
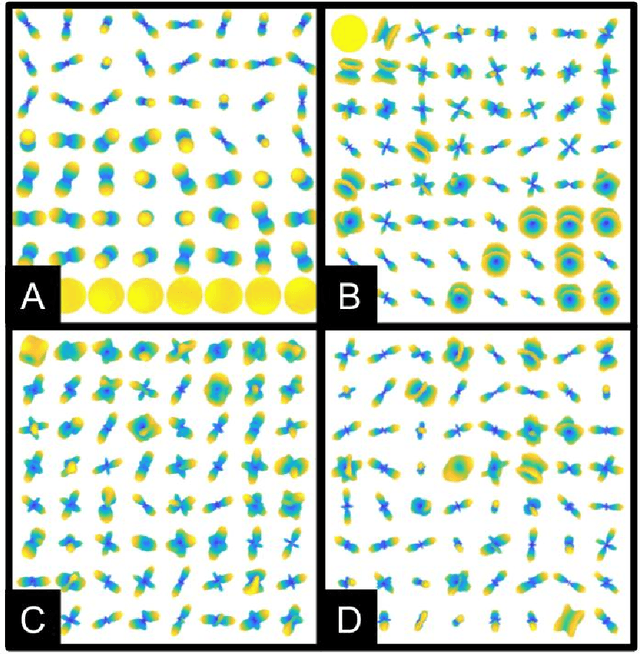
Regularization for matrix factorization (MF) and approximation problems has been carried out in many different ways. Due to its popularity in deep learning, dropout has been applied also for this class of problems. Despite its solid empirical performance, the theoretical properties of dropout as a regularizer remain quite elusive for this class of problems. In this paper, we present a theoretical analysis of dropout for MF, where Bernoulli random variables are used to drop columns of the factors. We demonstrate the equivalence between dropout and a fully deterministic model for MF in which the factors are regularized by the sum of the product of squared Euclidean norms of the columns. Additionally, we inspect the case of a variable sized factorization and we prove that dropout achieves the global minimum of a convex approximation problem with (squared) nuclear norm regularization. As a result, we conclude that dropout can be used as a low-rank regularizer with data dependent singular-value thresholding.