GRASP: Accelerating Shortest Path Attacks via Graph Attention

Recent advances in machine learning (ML) have shown promise in aiding and accelerating classical combinatorial optimization algorithms. ML-based speed ups that aim to learn in an end to end manner (i.e., directly output the solution) tend to trade off run time with solution quality. Therefore, solutions that are able to accelerate existing solvers while maintaining their performance guarantees, are of great interest. We consider an APX-hard problem, where an adversary aims to attack shortest paths in a graph by removing the minimum number of edges. We propose the GRASP algorithm: Graph Attention Accelerated Shortest Path Attack, an ML aided optimization algorithm that achieves run times up to 10x faster, while maintaining the quality of solution generated. GRASP uses a graph attention network to identify a smaller subgraph containing the combinatorial solution, thus effectively reducing the input problem size. Additionally, we demonstrate how careful representation of the input graph, including node features that correlate well with the optimization task, can highlight important structure in the optimization solution.

Graph-SCP: Accelerating Set Cover Problems with Graph Neural Networks

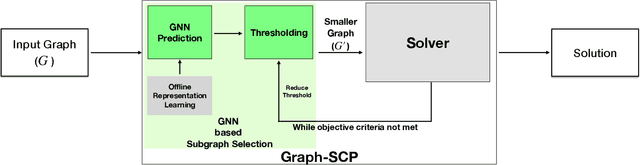
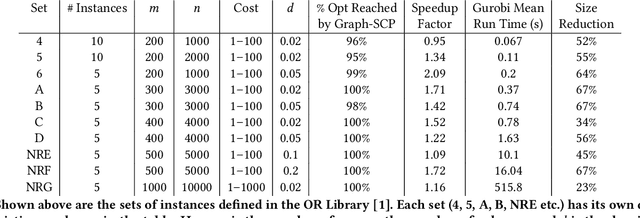
Machine learning (ML) approaches are increasingly being used to accelerate combinatorial optimization (CO) problems. We look specifically at the Set Cover Problem (SCP) and propose Graph-SCP, a graph neural network method that can augment existing optimization solvers by learning to identify a much smaller sub-problem that contains the solution space. We evaluate the performance of Graph-SCP on synthetic weighted and unweighted SCP instances with diverse problem characteristics and complexities, and on instances from the OR Library, a canonical benchmark for SCP. We show that Graph-SCP reduces the problem size by 30-70% and achieves run time speedups up to~25x when compared to commercial solvers (Gurobi). Given a desired optimality threshold, Graph-SCP will improve upon it or even achieve 100% optimality. This is in contrast to fast greedy solutions that significantly compromise solution quality to achieve guaranteed polynomial run time. Graph-SCP can generalize to larger problem sizes and can be used with other conventional or ML-augmented CO solvers to lead to potential additional run time improvement.

Topological Effects on Attacks Against Vertex Classification

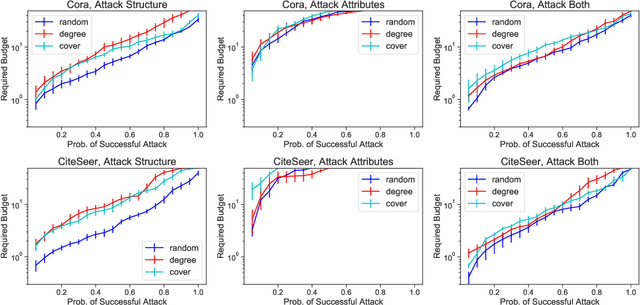
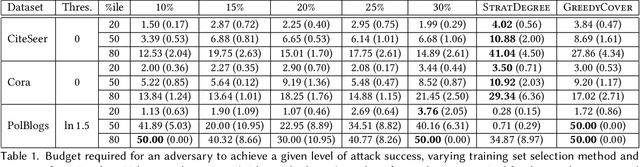
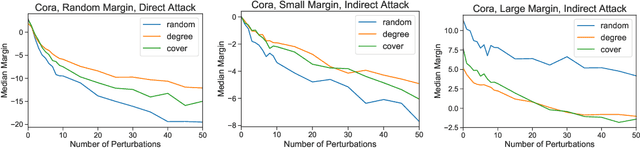
Vertex classification is vulnerable to perturbations of both graph topology and vertex attributes, as shown in recent research. As in other machine learning domains, concerns about robustness to adversarial manipulation can prevent potential users from adopting proposed methods when the consequence of action is very high. This paper considers two topological characteristics of graphs and explores the way these features affect the amount the adversary must perturb the graph in order to be successful. We show that, if certain vertices are included in the training set, it is possible to substantially an adversary's required perturbation budget. On four citation datasets, we demonstrate that if the training set includes high degree vertices or vertices that ensure all unlabeled nodes have neighbors in the training set, we show that the adversary's budget often increases by a substantial factor---often a factor of 2 or more---over random training for the Nettack poisoning attack. Even for especially easy targets (those that are misclassified after just one or two perturbations), the degradation of performance is much slower, assigning much lower probabilities to the incorrect classes. In addition, we demonstrate that this robustness either persists when recently proposed defenses are applied, or is competitive with the resulting performance improvement for the defender.

Assessing Functional Neural Connectivity as an Indicator of Cognitive Performance

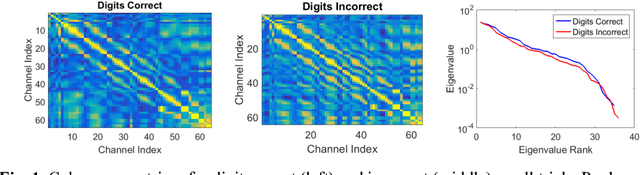
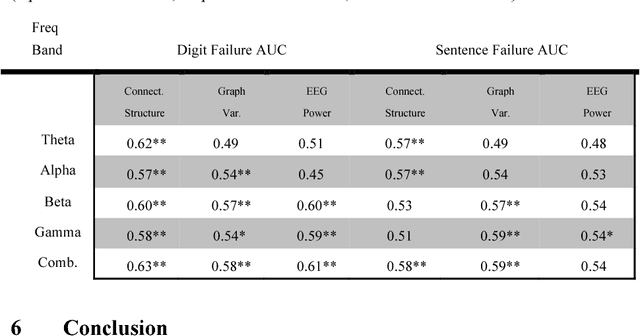
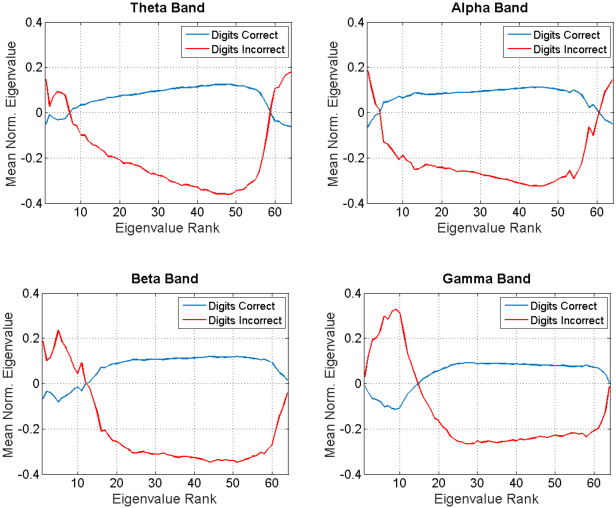
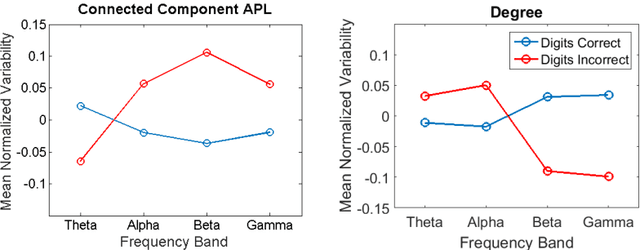
Studies in recent years have demonstrated that neural organization and structure impact an individual's ability to perform a given task. Specifically, individuals with greater neural efficiency have been shown to outperform those with less organized functional structure. In this work, we compare the predictive ability of properties of neural connectivity on a working memory task. We provide two novel approaches for characterizing functional network connectivity from electroencephalography (EEG), and compare these features to the average power across frequency bands in EEG channels. Our first novel approach represents functional connectivity structure through the distribution of eigenvalues making up channel coherence matrices in multiple frequency bands. Our second approach creates a connectivity network at each frequency band, and assesses variability in average path lengths of connected components and degree across the network. Failures in digit and sentence recall on single trials are detected using a Gaussian classifier for each feature set, at each frequency band. The classifier results are then fused across frequency bands, with the resulting detection performance summarized using the area under the receiver operating characteristic curve (AUC) statistic. Fused AUC results of 0.63/0.58/0.61 for digit recall failure and 0.58/0.59/0.54 for sentence recall failure are obtained from the connectivity structure, graph variability, and channel power features respectively.

A Spectral Framework for Anomalous Subgraph Detection

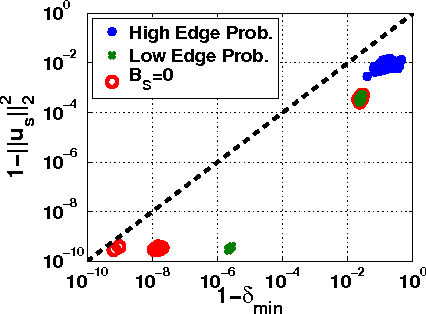
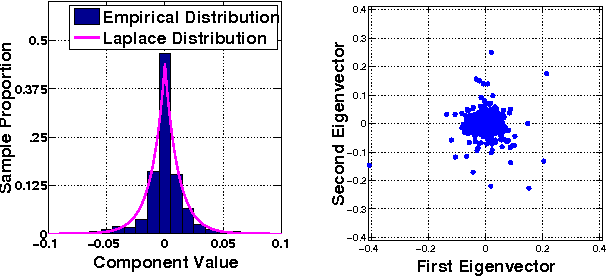
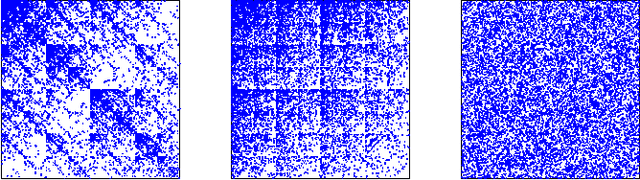
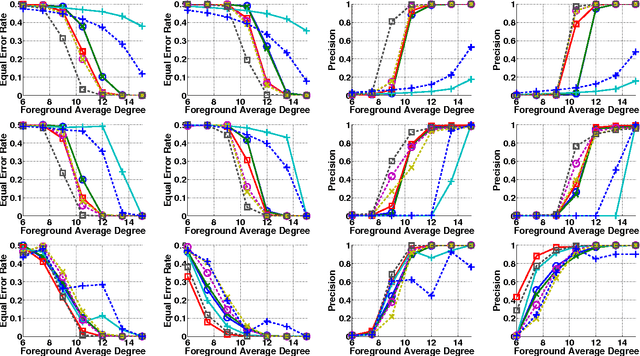
A wide variety of application domains are concerned with data consisting of entities and their relationships or connections, formally represented as graphs. Within these diverse application areas, a common problem of interest is the detection of a subset of entities whose connectivity is anomalous with respect to the rest of the data. While the detection of such anomalous subgraphs has received a substantial amount of attention, no application-agnostic framework exists for analysis of signal detectability in graph-based data. In this paper, we describe a framework that enables such analysis using the principal eigenspace of a graph's residuals matrix, commonly called the modularity matrix in community detection. Leveraging this analytical tool, we show that the framework has a natural power metric in the spectral norm of the anomalous subgraph's adjacency matrix (signal power) and of the background graph's residuals matrix (noise power). We propose several algorithms based on spectral properties of the residuals matrix, with more computationally expensive techniques providing greater detection power. Detection and identification performance are presented for a number of signal and noise models, including clusters and bipartite foregrounds embedded into simple random backgrounds as well as graphs with community structure and realistic degree distributions. The trends observed verify intuition gleaned from other signal processing areas, such as greater detection power when the signal is embedded within a less active portion of the background. We demonstrate the utility of the proposed techniques in detecting small, highly anomalous subgraphs in real graphs derived from Internet traffic and product co-purchases.