Patrick J. Wolfe
A Spectral Framework for Anomalous Subgraph Detection
Oct 22, 2014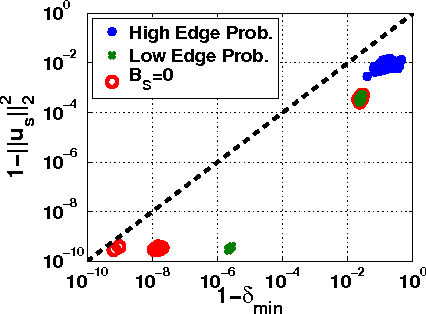
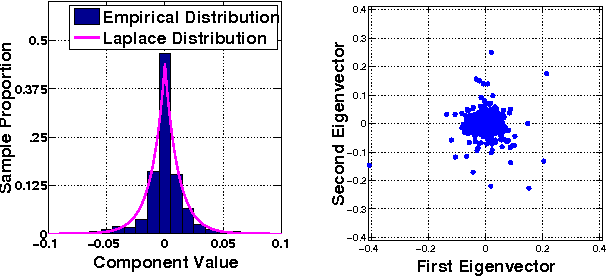
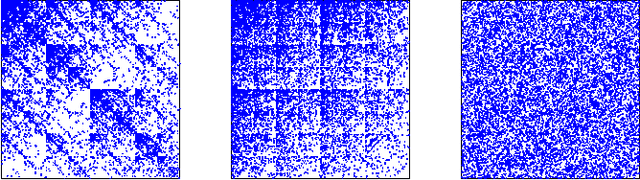
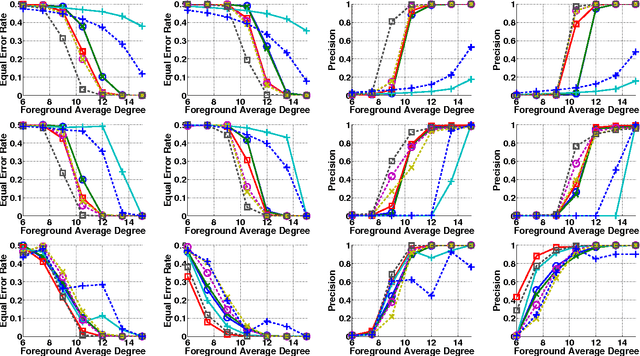
Abstract:A wide variety of application domains are concerned with data consisting of entities and their relationships or connections, formally represented as graphs. Within these diverse application areas, a common problem of interest is the detection of a subset of entities whose connectivity is anomalous with respect to the rest of the data. While the detection of such anomalous subgraphs has received a substantial amount of attention, no application-agnostic framework exists for analysis of signal detectability in graph-based data. In this paper, we describe a framework that enables such analysis using the principal eigenspace of a graph's residuals matrix, commonly called the modularity matrix in community detection. Leveraging this analytical tool, we show that the framework has a natural power metric in the spectral norm of the anomalous subgraph's adjacency matrix (signal power) and of the background graph's residuals matrix (noise power). We propose several algorithms based on spectral properties of the residuals matrix, with more computationally expensive techniques providing greater detection power. Detection and identification performance are presented for a number of signal and noise models, including clusters and bipartite foregrounds embedded into simple random backgrounds as well as graphs with community structure and realistic degree distributions. The trends observed verify intuition gleaned from other signal processing areas, such as greater detection power when the signal is embedded within a less active portion of the background. We demonstrate the utility of the proposed techniques in detecting small, highly anomalous subgraphs in real graphs derived from Internet traffic and product co-purchases.
* In submission to the IEEE, 16 pages, 8 figures
Co-clustering separately exchangeable network data
Jan 16, 2014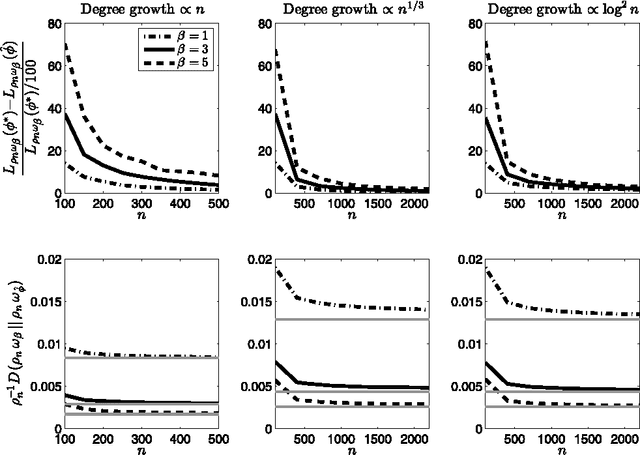
Abstract:This article establishes the performance of stochastic blockmodels in addressing the co-clustering problem of partitioning a binary array into subsets, assuming only that the data are generated by a nonparametric process satisfying the condition of separate exchangeability. We provide oracle inequalities with rate of convergence $\mathcal{O}_P(n^{-1/4})$ corresponding to profile likelihood maximization and mean-square error minimization, and show that the blockmodel can be interpreted in this setting as an optimal piecewise-constant approximation to the generative nonparametric model. We also show for large sample sizes that the detection of co-clusters in such data indicates with high probability the existence of co-clusters of equal size and asymptotically equivalent connectivity in the underlying generative process.
* Published in at http://dx.doi.org/10.1214/13-AOS1173 the Annals of Statistics (http://www.imstat.org/aos/) by the Institute of Mathematical Statistics (http://www.imstat.org)
Stochastic blockmodels with growing number of classes
Apr 30, 2011


Abstract:We present asymptotic and finite-sample results on the use of stochastic blockmodels for the analysis of network data. We show that the fraction of misclassified network nodes converges in probability to zero under maximum likelihood fitting when the number of classes is allowed to grow as the root of the network size and the average network degree grows at least poly-logarithmically in this size. We also establish finite-sample confidence bounds on maximum-likelihood blockmodel parameter estimates from data comprising independent Bernoulli random variates; these results hold uniformly over class assignment. We provide simulations verifying the conditions sufficient for our results, and conclude by fitting a logit parameterization of a stochastic blockmodel with covariates to a network data example comprising a collection of Facebook profiles, resulting in block estimates that reveal residual structure.
* 12 pages, 3 figures; revised version
Likelihood-based semi-supervised model selection with applications to speech processing
Nov 20, 2009


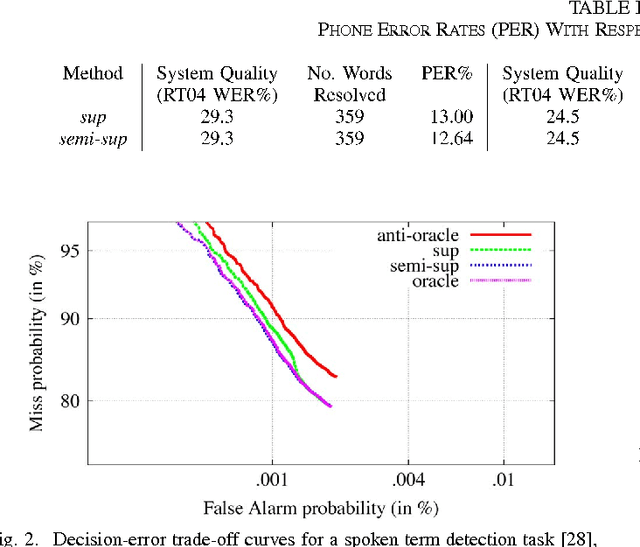
Abstract:In conventional supervised pattern recognition tasks, model selection is typically accomplished by minimizing the classification error rate on a set of so-called development data, subject to ground-truth labeling by human experts or some other means. In the context of speech processing systems and other large-scale practical applications, however, such labeled development data are typically costly and difficult to obtain. This article proposes an alternative semi-supervised framework for likelihood-based model selection that leverages unlabeled data by using trained classifiers representing each model to automatically generate putative labels. The errors that result from this automatic labeling are shown to be amenable to results from robust statistics, which in turn provide for minimax-optimal censored likelihood ratio tests that recover the nonparametric sign test as a limiting case. This approach is then validated experimentally using a state-of-the-art automatic speech recognition system to select between candidate word pronunciations using unlabeled speech data that only potentially contain instances of the words under test. Results provide supporting evidence for the utility of this approach, and suggest that it may also find use in other applications of machine learning.
* 11 pages, 2 figures; submitted for publication
On landmark selection and sampling in high-dimensional data analysis
Jun 24, 2009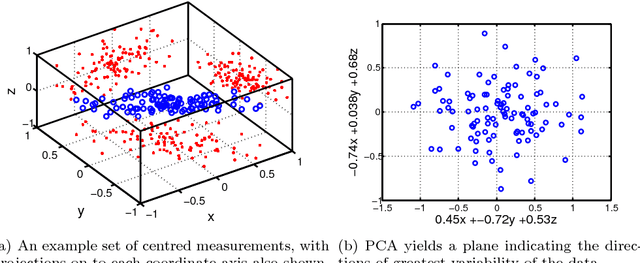
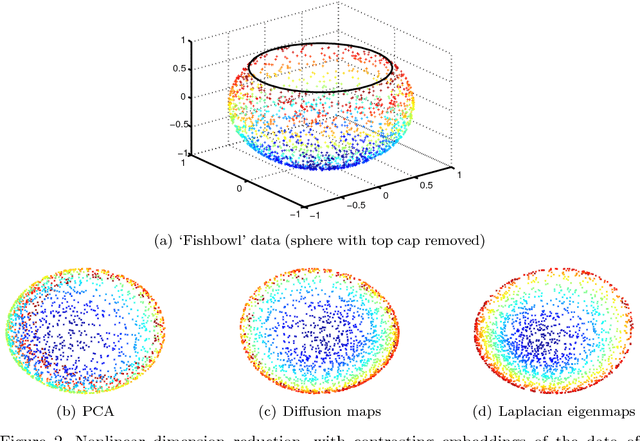


Abstract:In recent years, the spectral analysis of appropriately defined kernel matrices has emerged as a principled way to extract the low-dimensional structure often prevalent in high-dimensional data. Here we provide an introduction to spectral methods for linear and nonlinear dimension reduction, emphasizing ways to overcome the computational limitations currently faced by practitioners with massive datasets. In particular, a data subsampling or landmark selection process is often employed to construct a kernel based on partial information, followed by an approximate spectral analysis termed the Nystrom extension. We provide a quantitative framework to analyse this procedure, and use it to demonstrate algorithmic performance bounds on a range of practical approaches designed to optimize the landmark selection process. We compare the practical implications of these bounds by way of real-world examples drawn from the field of computer vision, whereby low-dimensional manifold structure is shown to emerge from high-dimensional video data streams.
* 18 pages, 6 figures, submitted for publication
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge