Control Theoretic Approach to Fine-Tuning and Transfer Learning

Given a training set in the form of a paired $(\mathcal{X},\mathcal{Y})$, we say that the control system $\dot{x} = f(x,u)$ has learned the paired set via the control $u^*$ if the system steers each point of $\mathcal{X}$ to its corresponding target in $\mathcal{Y}$. Most existing methods for finding a control function $u^*$ require learning of a new control function if the training set is updated. To overcome this limitation, we introduce the concept of $\textit{tuning without forgetting}$. We develop $\textit{an iterative algorithm}$ to tune the control function $u^*$ when the training set expands, whereby points already in the paired set are still matched, and new training samples are learned. More specifically, at each update of our method, the control $u^*$ is projected onto the kernel of the end-point mapping generated by the controlled dynamics at the learned samples. It ensures keeping the end points for the previously learned samples constant while iteratively learning additional samples. Our work contributes to the scalability of control methods, offering a novel approach to adaptively handle training set expansions.

Geometric Heat Flow Method for Legged Locomotion Planning

We propose in this paper a motion planning method for legged robot locomotion based on Geometric Heat Flow framework. The motion planning task is challenging due to the hybrid nature of dynamics and contact constraints. We encode the hybrid dynamics and constraints into Riemannian inner product, and this inner product is defined so that short curves correspond to admissible motions for the system. We rely on the affine geometric heat flow to deform an arbitrary path connecting the desired initial and final states to this admissible motion. The method is able to automatically find the trajectory of robot's center of mass, feet contact positions and forces on uneven terrain.

Vision-Based Shape Reconstruction of Soft Continuum Arms Using a Geometric Strain Parametrization

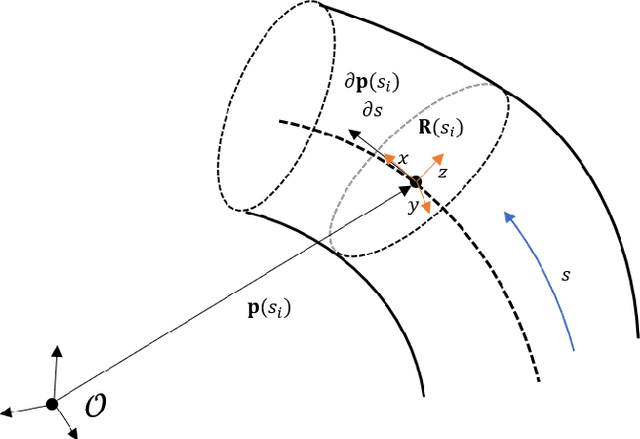
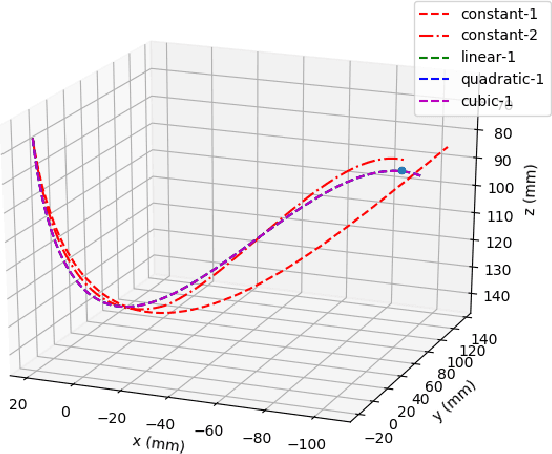
Interest in soft continuum arms has increased as their inherent material elasticity enables safe and adaptive interactions with the environment. However to achieve full autonomy in these arms, accurate three-dimensional shape sensing is needed. Vision-based solutions have been found to be effective in estimating the shape of soft continuum arms. In this paper, a vision-based shape estimator that utilizes a geometric strain based representation for the soft continuum arm's shape, is proposed. This representation reduces the dimension of the curved shape to a finite set of strain basis functions, thereby allowing for efficient optimization for the shape that best fits the observed image. Experimental results demonstrate the effectiveness of the proposed approach in estimating the end effector with accuracy less than the soft arm's radius. Multiple basis functions are also analyzed and compared for the specific soft continuum arm in use.

On landmark selection and sampling in high-dimensional data analysis

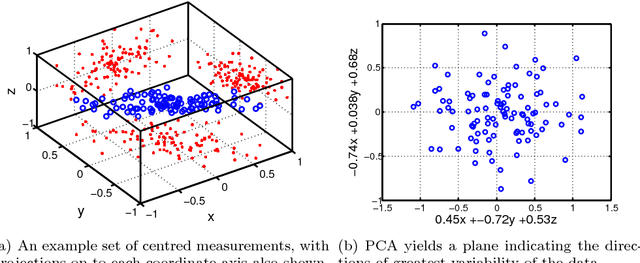
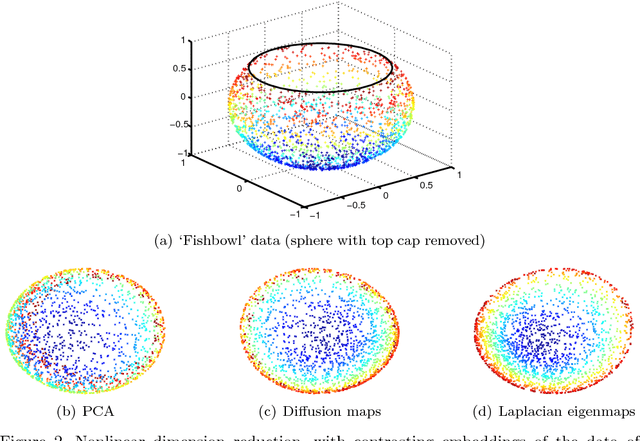
In recent years, the spectral analysis of appropriately defined kernel matrices has emerged as a principled way to extract the low-dimensional structure often prevalent in high-dimensional data. Here we provide an introduction to spectral methods for linear and nonlinear dimension reduction, emphasizing ways to overcome the computational limitations currently faced by practitioners with massive datasets. In particular, a data subsampling or landmark selection process is often employed to construct a kernel based on partial information, followed by an approximate spectral analysis termed the Nystrom extension. We provide a quantitative framework to analyse this procedure, and use it to demonstrate algorithmic performance bounds on a range of practical approaches designed to optimize the landmark selection process. We compare the practical implications of these bounds by way of real-world examples drawn from the field of computer vision, whereby low-dimensional manifold structure is shown to emerge from high-dimensional video data streams.