Studying the Impact of Latent Representations in Implicit Neural Networks for Scientific Continuous Field Reconstruction

Learning a continuous and reliable representation of physical fields from sparse sampling is challenging and it affects diverse scientific disciplines. In a recent work, we present a novel model called MMGN (Multiplicative and Modulated Gabor Network) with implicit neural networks. In this work, we design additional studies leveraging explainability methods to complement the previous experiments and further enhance the understanding of latent representations generated by the model. The adopted methods are general enough to be leveraged for any latent space inspection. Preliminary results demonstrate the contextual information incorporated in the latent representations and their impact on the model performance. As a work in progress, we will continue to verify our findings and develop novel explainability approaches.

Continuous Field Reconstruction from Sparse Observations with Implicit Neural Networks

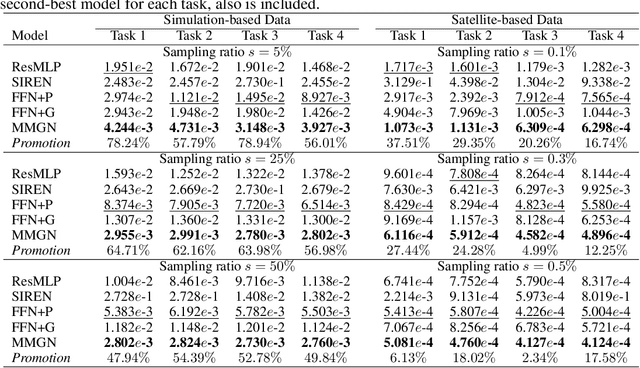
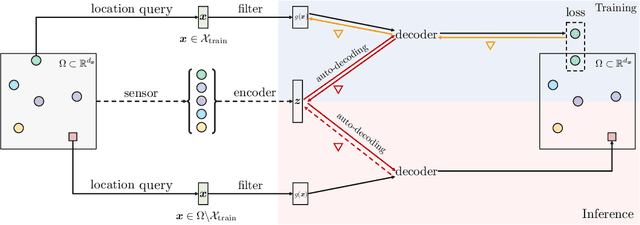
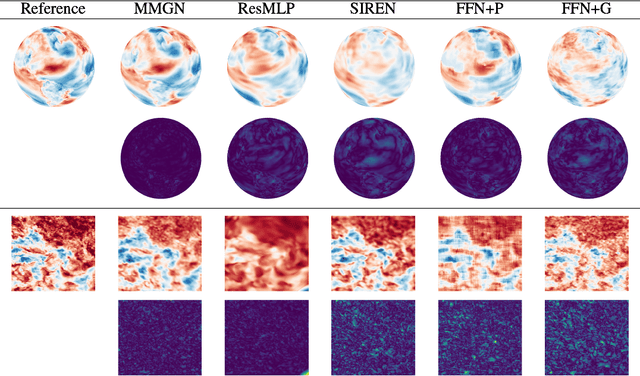
Reliably reconstructing physical fields from sparse sensor data is a challenge that frequently arises in many scientific domains. In practice, the process generating the data often is not understood to sufficient accuracy. Therefore, there is a growing interest in using the deep neural network route to address the problem. This work presents a novel approach that learns a continuous representation of the physical field using implicit neural representations (INRs). Specifically, after factorizing spatiotemporal variability into spatial and temporal components using the separation of variables technique, the method learns relevant basis functions from sparsely sampled irregular data points to develop a continuous representation of the data. In experimental evaluations, the proposed model outperforms recent INR methods, offering superior reconstruction quality on simulation data from a state-of-the-art climate model and a second dataset that comprises ultra-high resolution satellite-based sea surface temperature fields.

Surrogate Neural Networks to Estimate Parametric Sensitivity of Ocean Models

Modeling is crucial to understanding the effect of greenhouse gases, warming, and ice sheet melting on the ocean. At the same time, ocean processes affect phenomena such as hurricanes and droughts. Parameters in the models that cannot be physically measured have a significant effect on the model output. For an idealized ocean model, we generated perturbed parameter ensemble data and trained surrogate neural network models. The neural surrogates accurately predicted the one-step forward dynamics, of which we then computed the parametric sensitivity.

A New Spectral Clustering Algorithm

We present a new clustering algorithm that is based on searching for natural gaps in the components of the lowest energy eigenvectors of the Laplacian of a graph. In comparing the performance of the proposed method with a set of other popular methods (KMEANS, spectral-KMEANS, and an agglomerative method) in the context of the Lancichinetti-Fortunato-Radicchi (LFR) Benchmark for undirected weighted overlapping networks, we find that the new method outperforms the other spectral methods considered in certain parameter regimes. Finally, in an application to climate data involving one of the most important modes of interannual climate variability, the El Nino Southern Oscillation phenomenon, we demonstrate the ability of the new algorithm to readily identify different flavors of the phenomenon.