Neural-Brane: Neural Bayesian Personalized Ranking for Attributed Network Embedding

Network embedding methodologies, which learn a distributed vector representation for each vertex in a network, have attracted considerable interest in recent years. Existing works have demonstrated that vertex representation learned through an embedding method provides superior performance in many real-world applications, such as node classification, link prediction, and community detection. However, most of the existing methods for network embedding only utilize topological information of a vertex, ignoring a rich set of nodal attributes (such as, user profiles of an online social network, or textual contents of a citation network), which is abundant in all real-life networks. A joint network embedding that takes into account both attributional and relational information entails a complete network information and could further enrich the learned vector representations. In this work, we present Neural-Brane, a novel Neural Bayesian Personalized Ranking based Attributed Network Embedding. For a given network, Neural-Brane extracts latent feature representation of its vertices using a designed neural network model that unifies network topological information and nodal attributes; Besides, it utilizes Bayesian personalized ranking objective, which exploits the proximity ordering between a similar node-pair and a dissimilar node-pair. We evaluate the quality of vertex embedding produced by Neural-Brane by solving the node classification and clustering tasks on four real-world datasets. Experimental results demonstrate the superiority of our proposed method over the state-of-the-art existing methods.

Incremental Eigenpair Computation for Graph Laplacian Matrices: Theory and Applications

The smallest eigenvalues and the associated eigenvectors (i.e., eigenpairs) of a graph Laplacian matrix have been widely used in spectral clustering and community detection. However, in real-life applications the number of clusters or communities (say, $K$) is generally unknown a-priori. Consequently, the majority of the existing methods either choose $K$ heuristically or they repeat the clustering method with different choices of $K$ and accept the best clustering result. The first option, more often, yields suboptimal result, while the second option is computationally expensive. In this work, we propose an incremental method for constructing the eigenspectrum of the graph Laplacian matrix. This method leverages the eigenstructure of graph Laplacian matrix to obtain the $K$-th smallest eigenpair of the Laplacian matrix given a collection of all previously computed $K-1$ smallest eigenpairs. Our proposed method adapts the Laplacian matrix such that the batch eigenvalue decomposition problem transforms into an efficient sequential leading eigenpair computation problem. As a practical application, we consider user-guided spectral clustering. Specifically, we demonstrate that users can utilize the proposed incremental method for effective eigenpair computation and for determining the desired number of clusters based on multiple clustering metrics.

Name Disambiguation in Anonymized Graphs using Network Embedding

In real-world, our DNA is unique but many people share names. This phenomenon often causes erroneous aggregation of documents of multiple persons who are namesake of one another. Such mistakes deteriorate the performance of document retrieval, web search, and more seriously, cause improper attribution of credit or blame in digital forensic. To resolve this issue, the name disambiguation task is designed which aims to partition the documents associated with a name reference such that each partition contains documents pertaining to a unique real-life person. Existing solutions to this task substantially rely on feature engineering, such as biographical feature extraction, or construction of auxiliary features from Wikipedia. However, for many scenarios, such features may be costly to obtain or unavailable due to the risk of privacy violation. In this work, we propose a novel name disambiguation method. Our proposed method is non-intrusive of privacy because instead of using attributes pertaining to a real-life person, our method leverages only relational data in the form of anonymized graphs. In the methodological aspect, the proposed method uses a novel representation learning model to embed each document in a low dimensional vector space where name disambiguation can be solved by a hierarchical agglomerative clustering algorithm. Our experimental results demonstrate that the proposed method is significantly better than the existing name disambiguation methods working in a similar setting.

Feature Selection for Classification under Anonymity Constraint

Over the last decade, proliferation of various online platforms and their increasing adoption by billions of users have heightened the privacy risk of a user enormously. In fact, security researchers have shown that sparse microdata containing information about online activities of a user although anonymous, can still be used to disclose the identity of the user by cross-referencing the data with other data sources. To preserve the privacy of a user, in existing works several methods (k-anonymity, l-diversity, differential privacy) are proposed that ensure a dataset which is meant to share or publish bears small identity disclosure risk. However, the majority of these methods modify the data in isolation, without considering their utility in subsequent knowledge discovery tasks, which makes these datasets less informative. In this work, we consider labeled data that are generally used for classification, and propose two methods for feature selection considering two goals: first, on the reduced feature set the data has small disclosure risk, and second, the utility of the data is preserved for performing a classification task. Experimental results on various real-world datasets show that the method is effective and useful in practice.

Incremental Method for Spectral Clustering of Increasing Orders

The smallest eigenvalues and the associated eigenvectors (i.e., eigenpairs) of a graph Laplacian matrix have been widely used for spectral clustering and community detection. However, in real-life applications the number of clusters or communities (say, $K$) is generally unknown a-priori. Consequently, the majority of the existing methods either choose $K$ heuristically or they repeat the clustering method with different choices of $K$ and accept the best clustering result. The first option, more often, yields suboptimal result, while the second option is computationally expensive. In this work, we propose an incremental method for constructing the eigenspectrum of the graph Laplacian matrix. This method leverages the eigenstructure of graph Laplacian matrix to obtain the $K$-th eigenpairs of the Laplacian matrix given a collection of all the $K-1$ smallest eigenpairs. Our proposed method adapts the Laplacian matrix such that the batch eigenvalue decomposition problem transforms into an efficient sequential leading eigenpair computation problem. As a practical application, we consider user-guided spectral clustering. Specifically, we demonstrate that users can utilize the proposed incremental method for effective eigenpair computation and determining the desired number of clusters based on multiple clustering metrics.

Trust from the past: Bayesian Personalized Ranking based Link Prediction in Knowledge Graphs

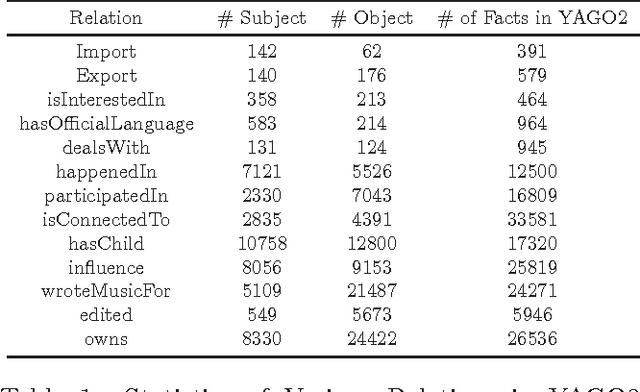
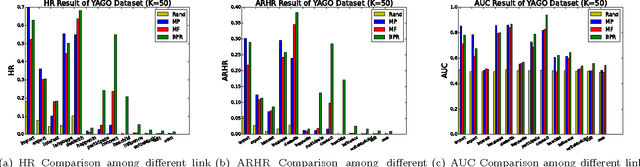
Link prediction, or predicting the likelihood of a link in a knowledge graph based on its existing state is a key research task. It differs from a traditional link prediction task in that the links in a knowledge graph are categorized into different predicates and the link prediction performance of different predicates in a knowledge graph generally varies widely. In this work, we propose a latent feature embedding based link prediction model which considers the prediction task for each predicate disjointly. To learn the model parameters it utilizes a Bayesian personalized ranking based optimization technique. Experimental results on large-scale knowledge bases such as YAGO2 show that our link prediction approach achieves substantially higher performance than several state-of-art approaches. We also show that for a given predicate the topological properties of the knowledge graph induced by the given predicate edges are key indicators of the link prediction performance of that predicate in the knowledge graph.