Interpretability of Epidemiological Models : The Curse of Non-Identifiability

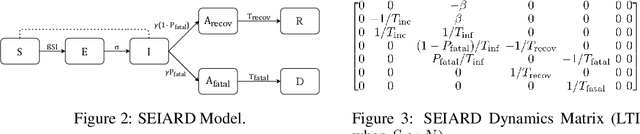
Interpretability of epidemiological models is a key consideration, especially when these models are used in a public health setting. Interpretability is strongly linked to the identifiability of the underlying model parameters, i.e., the ability to estimate parameter values with high confidence given observations. In this paper, we define three separate notions of identifiability that explore the different roles played by the model definition, the loss function, the fitting methodology, and the quality and quantity of data. We define an epidemiological compartmental model framework in which we highlight these non-identifiability issues and their mitigation.

A Multi-Arm Bandit Approach To Subset Selection Under Constraints

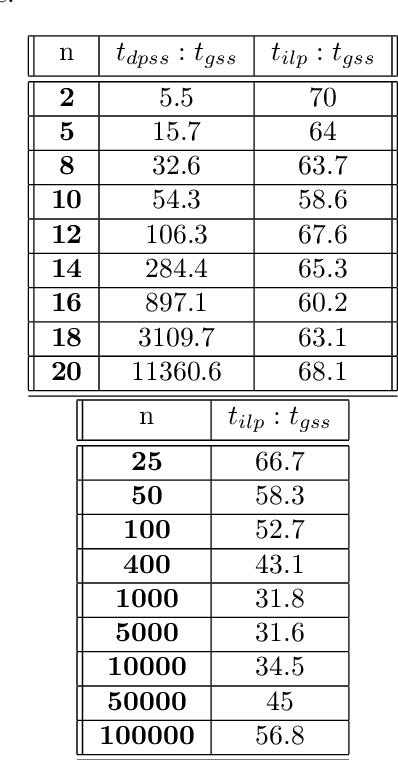
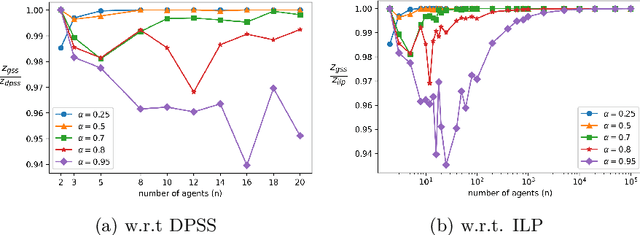
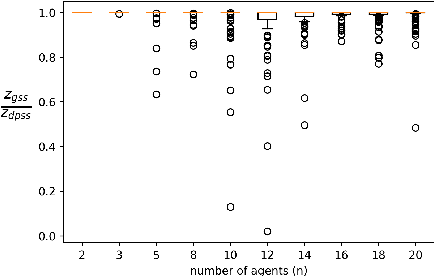
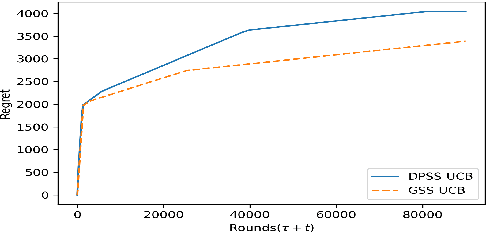
We explore the class of problems where a central planner needs to select a subset of agents, each with different quality and cost. The planner wants to maximize its utility while ensuring that the average quality of the selected agents is above a certain threshold. When the agents' quality is known, we formulate our problem as an integer linear program (ILP) and propose a deterministic algorithm, namely \dpss\ that provides an exact solution to our ILP. We then consider the setting when the qualities of the agents are unknown. We model this as a Multi-Arm Bandit (MAB) problem and propose \newalgo\ to learn the qualities over multiple rounds. We show that after a certain number of rounds, $\tau$, \newalgo\ outputs a subset of agents that satisfy the average quality constraint with a high probability. Next, we provide bounds on $\tau$ and prove that after $\tau$ rounds, the algorithm incurs a regret of $O(\ln T)$, where $T$ is the total number of rounds. We further illustrate the efficacy of \newalgo\ through simulations. To overcome the computational limitations of \dpss, we propose a polynomial-time greedy algorithm, namely \greedy, that provides an approximate solution to our ILP. We also compare the performance of \dpss\ and \greedy\ through experiments.