Interpretability of Epidemiological Models : The Curse of Non-Identifiability

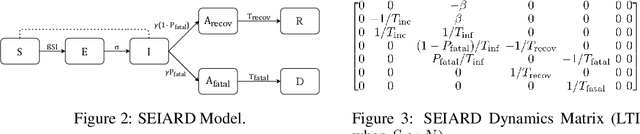
Interpretability of epidemiological models is a key consideration, especially when these models are used in a public health setting. Interpretability is strongly linked to the identifiability of the underlying model parameters, i.e., the ability to estimate parameter values with high confidence given observations. In this paper, we define three separate notions of identifiability that explore the different roles played by the model definition, the loss function, the fitting methodology, and the quality and quantity of data. We define an epidemiological compartmental model framework in which we highlight these non-identifiability issues and their mitigation.

Sample Complexity Bounds for 1-bit Compressive Sensing and Binary Stable Embeddings with Generative Priors

The goal of standard 1-bit compressive sensing is to accurately recover an unknown sparse vector from binary-valued measurements, each indicating the sign of a linear function of the vector. Motivated by recent advances in compressive sensing with generative models, where a generative modeling assumption replaces the usual sparsity assumption, we study the problem of 1-bit compressive sensing with generative models. We first consider noiseless 1-bit measurements, and provide sample complexity bounds for approximate recovery under i.i.d.~Gaussian measurements and a Lipschitz continuous generative prior, as well as a near-matching algorithm-independent lower bound. Moreover, we demonstrate that the Binary $\epsilon$-Stable Embedding property, which characterizes the robustness of the reconstruction to measurement errors and noise, also holds for 1-bit compressive sensing with Lipschitz continuous generative models with sufficiently many Gaussian measurements. In addition, we apply our results to neural network generative models, and provide a proof-of-concept numerical experiment demonstrating significant improvements over sparsity-based approaches.