Theories of synaptic memory consolidation and intelligent plasticity for continual learning

Humans and animals learn throughout life. Such continual learning is crucial for intelligence. In this chapter, we examine the pivotal role plasticity mechanisms with complex internal synaptic dynamics could play in enabling this ability in neural networks. By surveying theoretical research, we highlight two fundamental enablers for continual learning. First, synaptic plasticity mechanisms must maintain and evolve an internal state over several behaviorally relevant timescales. Second, plasticity algorithms must leverage the internal state to intelligently regulate plasticity at individual synapses to facilitate the seamless integration of new memories while avoiding detrimental interference with existing ones. Our chapter covers successful applications of these principles to deep neural networks and underscores the significance of synaptic metaplasticity in sustaining continual learning capabilities. Finally, we outline avenues for further research to understand the brain's superb continual learning abilities and harness similar mechanisms for artificial intelligence systems.

Improving equilibrium propagation without weight symmetry through Jacobian homeostasis

Equilibrium propagation (EP) is a compelling alternative to the backpropagation of error algorithm (BP) for computing gradients of neural networks on biological or analog neuromorphic substrates. Still, the algorithm requires weight symmetry and infinitesimal equilibrium perturbations, i.e., nudges, to estimate unbiased gradients efficiently. Both requirements are challenging to implement in physical systems. Yet, whether and how weight asymmetry affects its applicability is unknown because, in practice, it may be masked by biases introduced through the finite nudge. To address this question, we study generalized EP, which can be formulated without weight symmetry, and analytically isolate the two sources of bias. For complex-differentiable non-symmetric networks, we show that the finite nudge does not pose a problem, as exact derivatives can still be estimated via a Cauchy integral. In contrast, weight asymmetry introduces bias resulting in low task performance due to poor alignment of EP's neuronal error vectors compared to BP. To mitigate this issue, we present a new homeostatic objective that directly penalizes functional asymmetries of the Jacobian at the network's fixed point. This homeostatic objective dramatically improves the network's ability to solve complex tasks such as ImageNet 32x32. Our results lay the theoretical groundwork for studying and mitigating the adverse effects of imperfections of physical networks on learning algorithms that rely on the substrate's relaxation dynamics.

Predictor networks and stop-grads provide implicit variance regularization in BYOL/SimSiam

Self-supervised learning (SSL) learns useful representations from unlabelled data by training networks to be invariant to pairs of augmented versions of the same input. Non-contrastive methods avoid collapse either by directly regularizing the covariance matrix of network outputs or through asymmetric loss architectures, two seemingly unrelated approaches. Here, by building on DirectPred, we lay out a theoretical framework that reconciles these two views. We derive analytical expressions for the representational learning dynamics in linear networks. By expressing them in the eigenspace of the embedding covariance matrix, where the solutions decouple, we reveal the mechanism and conditions that provide implicit variance regularization. These insights allow us to formulate a new isotropic loss function that equalizes eigenvalue contribution and renders learning more robust. Finally, we show empirically that our findings translate to nonlinear networks trained on CIFAR-10 and STL-10.

Model of the Weak Reset Process in HfOx Resistive Memory for Deep Learning Frameworks

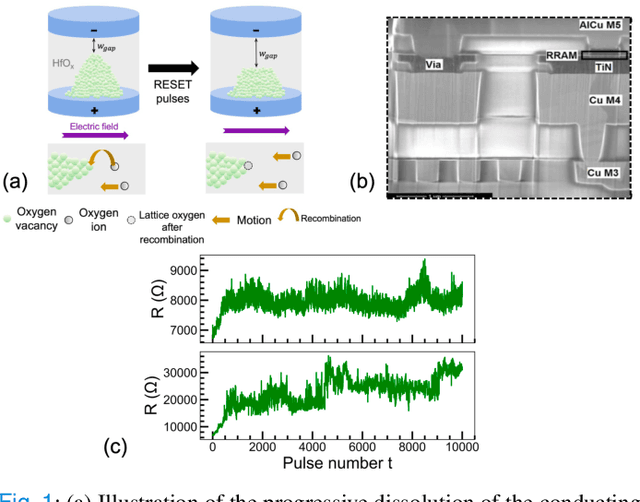
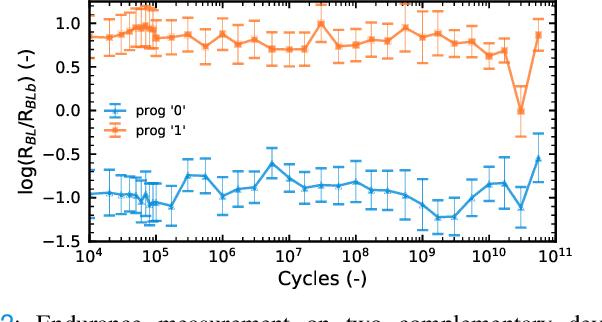
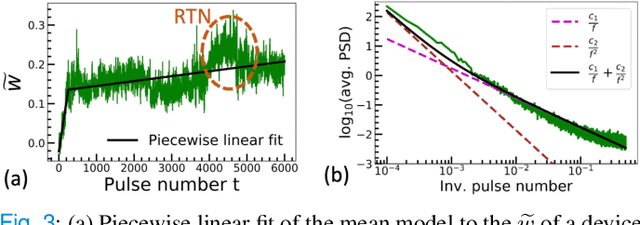
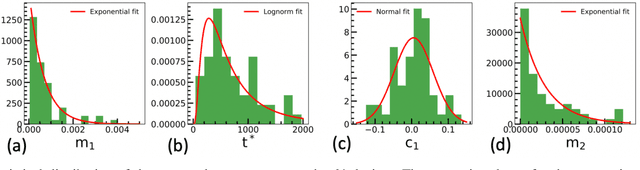
The implementation of current deep learning training algorithms is power-hungry, owing to data transfer between memory and logic units. Oxide-based RRAMs are outstanding candidates to implement in-memory computing, which is less power-intensive. Their weak RESET regime, is particularly attractive for learning, as it allows tuning the resistance of the devices with remarkable endurance. However, the resistive change behavior in this regime suffers many fluctuations and is particularly challenging to model, especially in a way compatible with tools used for simulating deep learning. In this work, we present a model of the weak RESET process in hafnium oxide RRAM and integrate this model within the PyTorch deep learning framework. Validated on experiments on a hybrid CMOS/RRAM technology, our model reproduces both the noisy progressive behavior and the device-to-device (D2D) variability. We use this tool to train Binarized Neural Networks for the MNIST handwritten digit recognition task and the CIFAR-10 object classification task. We simulate our model with and without various aspects of device imperfections to understand their impact on the training process and identify that the D2D variability is the most detrimental aspect. The framework can be used in the same manner for other types of memories to identify the device imperfections that cause the most degradation, which can, in turn, be used to optimize the devices to reduce the impact of these imperfections.

Synaptic metaplasticity in binarized neural networks

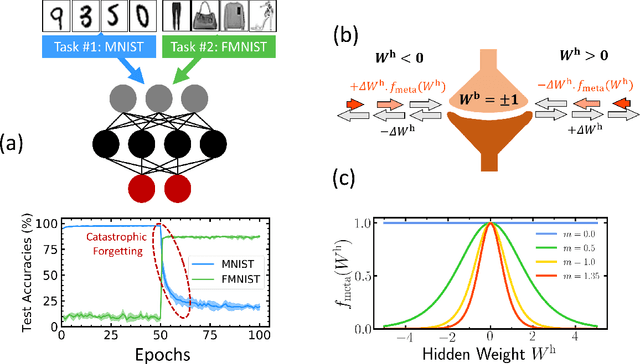
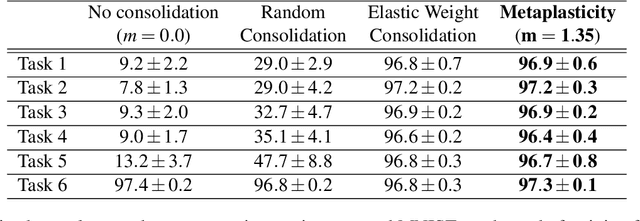
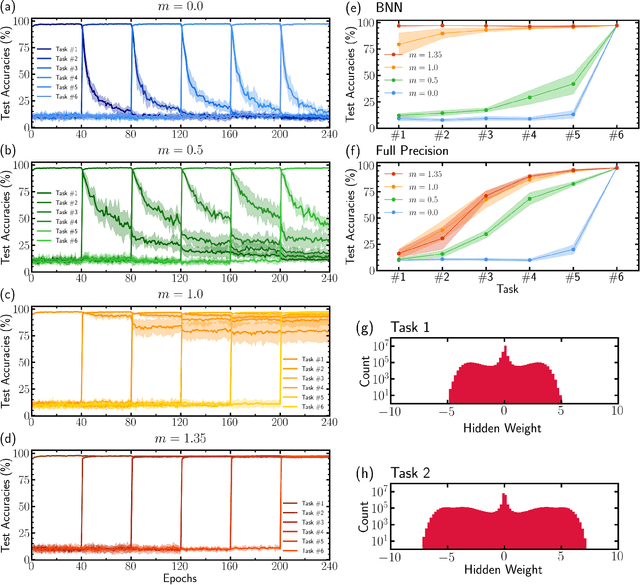
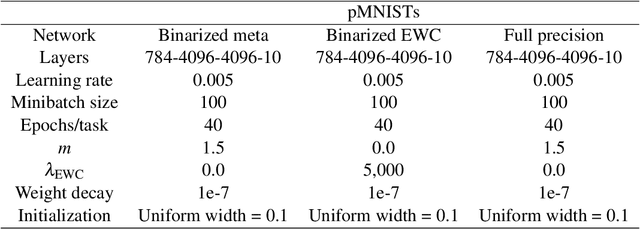
Unlike the brain, artificial neural networks, including state-of-the-art deep neural networks for computer vision, are subject to "catastrophic forgetting": they rapidly forget the previous task when trained on a new one. Neuroscience suggests that biological synapses avoid this issue through the process of synaptic consolidation and metaplasticity: the plasticity itself changes upon repeated synaptic events. In this work, we show that this concept of metaplasticity can be transferred to a particular type of deep neural networks, binarized neural networks, to reduce catastrophic forgetting.

Scaling Equilibrium Propagation to Deep ConvNets by Drastically Reducing its Gradient Estimator Bias

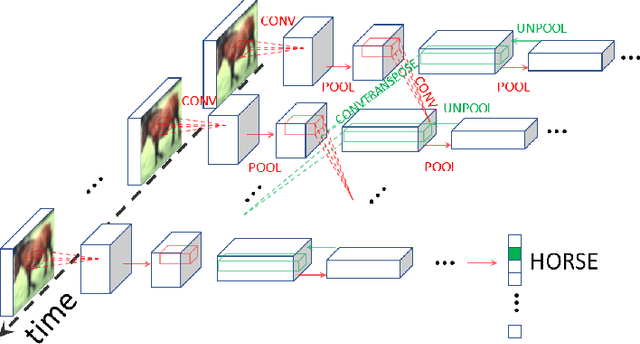
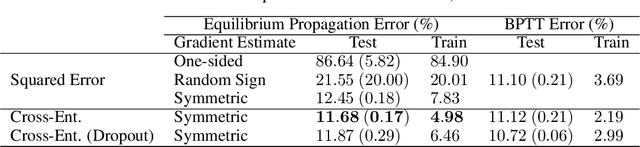
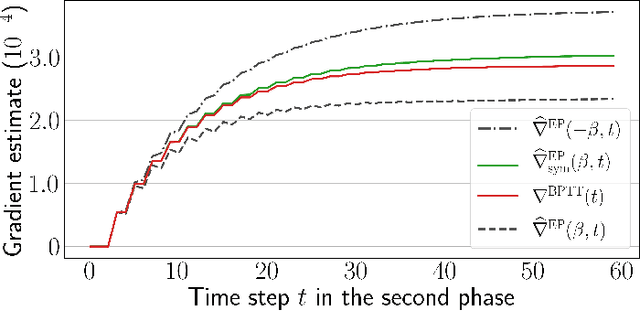
Equilibrium Propagation (EP) is a biologically-inspired counterpart of Backpropagation Through Time (BPTT) which, owing to its strong theoretical guarantees and the locality in space of its learning rule, fosters the design of energy-efficient hardware dedicated to learning. In practice, however, EP does not scale to visual tasks harder than MNIST. In this work, we show that a bias in the gradient estimate of EP, inherent in the use of finite nudging, is responsible for this phenomenon and that cancelling it allows training deep ConvNets by EP, including architectures with distinct forward and backward connections. These results highlight EP as a scalable approach to compute error gradients in deep neural networks, thereby motivating its hardware implementation.