Scaling Equilibrium Propagation to Deep ConvNets by Drastically Reducing its Gradient Estimator Bias
Paper and Code
Jan 14, 2021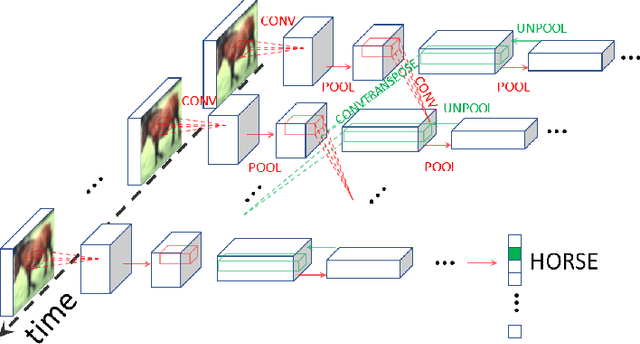
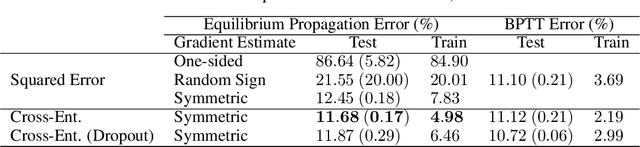
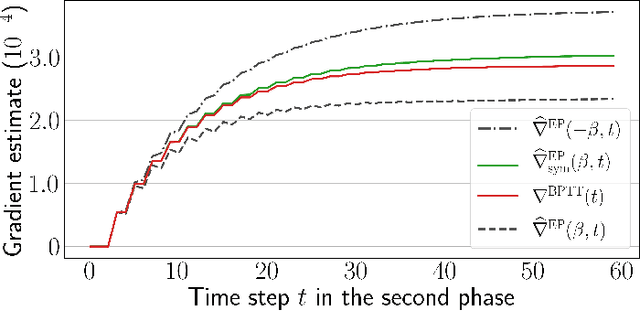

Equilibrium Propagation (EP) is a biologically-inspired counterpart of Backpropagation Through Time (BPTT) which, owing to its strong theoretical guarantees and the locality in space of its learning rule, fosters the design of energy-efficient hardware dedicated to learning. In practice, however, EP does not scale to visual tasks harder than MNIST. In this work, we show that a bias in the gradient estimate of EP, inherent in the use of finite nudging, is responsible for this phenomenon and that cancelling it allows training deep ConvNets by EP, including architectures with distinct forward and backward connections. These results highlight EP as a scalable approach to compute error gradients in deep neural networks, thereby motivating its hardware implementation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge