Efficient and Interpretable Robot Manipulation with Graph Neural Networks

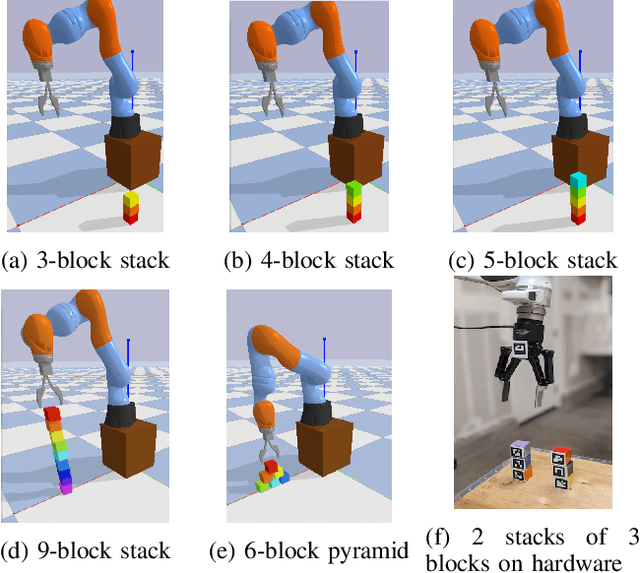
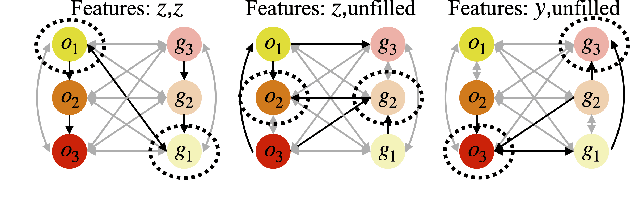
Many manipulation tasks can be naturally cast as a sequence of spatial relationships and constraints between objects. We aim to discover and scale these task-specific spatial relationships by representing manipulation tasks as operations over graphs. To do this, we pose manipulating a large, variable number of objects as a probabilistic classification problem over actions, objects and goals, learned using graph neural networks (GNNs). Our formulation first transforms the environment into a graph representation, then applies a trained GNN policy to predict which object to manipulate towards which goal state. Our GNN policies are trained using very few expert demonstrations on simple tasks, and exhibits generalization over number and configurations of objects in the environment and even to new, more complex tasks, and provide interpretable explanations for their decision-making. We present experiments which show that a single learned GNN policy can solve a variety of blockstacking tasks in both simulation and real hardware.

Encoding Physical Constraints in Differentiable Newton-Euler Algorithm

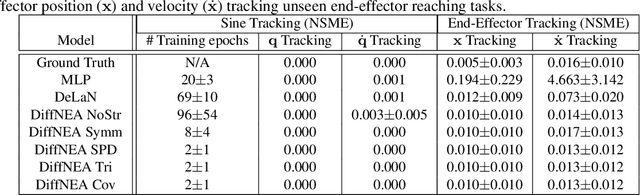
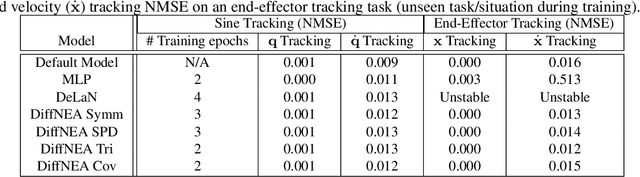
The recursive Newton-Euler Algorithm (RNEA) is a popular technique in robotics for computing the dynamics of robots. The computed dynamics can then be used for torque control with inverse dynamics, or for forward dynamics computations. RNEA can be framed as a differentiable computational graph, enabling the dynamics parameters of the robot to be learned from data via modern auto-differentiation toolboxes. However, the dynamics parameters learned in this manner can be physically implausible. In this work, we incorporate physical constraints in the learning by adding structure to the learned parameters. This results in a framework that can learn physically plausible dynamics via gradient descent, improving the training speed as well as generalization of the learned dynamics models. We evaluate our method on real-time inverse dynamics predictions of a 7 degree of freedom robot arm, both in simulation and on the real robot. Our experiments study a spectrum of structure added to learned dynamics, and compare their performance and generalization.