Encoding Physical Constraints in Differentiable Newton-Euler Algorithm

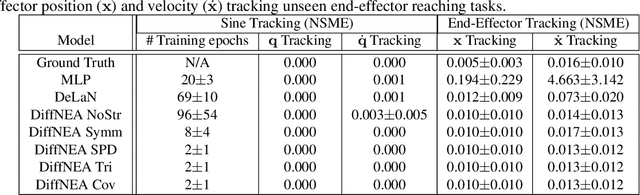
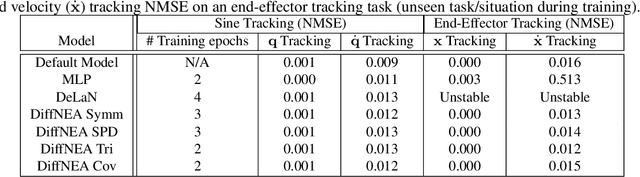
The recursive Newton-Euler Algorithm (RNEA) is a popular technique in robotics for computing the dynamics of robots. The computed dynamics can then be used for torque control with inverse dynamics, or for forward dynamics computations. RNEA can be framed as a differentiable computational graph, enabling the dynamics parameters of the robot to be learned from data via modern auto-differentiation toolboxes. However, the dynamics parameters learned in this manner can be physically implausible. In this work, we incorporate physical constraints in the learning by adding structure to the learned parameters. This results in a framework that can learn physically plausible dynamics via gradient descent, improving the training speed as well as generalization of the learned dynamics models. We evaluate our method on real-time inverse dynamics predictions of a 7 degree of freedom robot arm, both in simulation and on the real robot. Our experiments study a spectrum of structure added to learned dynamics, and compare their performance and generalization.