Deep Reinforcement Learning: A Convex Optimization Approach

In this paper, we consider reinforcement learning of nonlinear systems with continuous state and action spaces. We present an episodic learning algorithm, where we for each episode use convex optimization to find a two-layer neural network approximation of the optimal $Q$-function. The convex optimization approach guarantees that the weights calculated at each episode are optimal, with respect to the given sampled states and actions of the current episode. For stable nonlinear systems, we show that the algorithm converges and that the converging parameters of the trained neural network can be made arbitrarily close to the optimal neural network parameters. In particular, if the regularization parameter is $\rho$ and the time horizon is $T$, then the parameters of the trained neural network converge to $w$, where the distance between $w$ from the optimal parameters $w^\star$ is bounded by $\mathcal{O}(\rho T^{-1})$. That is, when the number of episodes goes to infinity, there exists a constant $C$ such that \[\|w-w^\star\| \le C\cdot\frac{\rho}{T}.\] In particular, our algorithm converges arbitrarily close to the optimal neural network parameters as the time horizon increases or as the regularization parameter decreases.

Decentralized Online Bandit Optimization on Directed Graphs with Regret Bounds

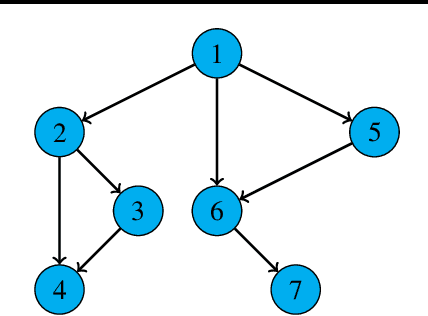
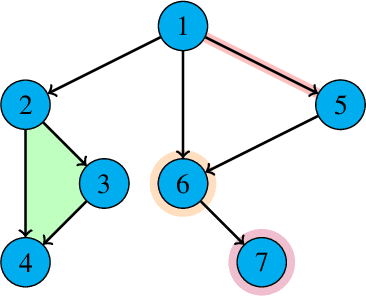
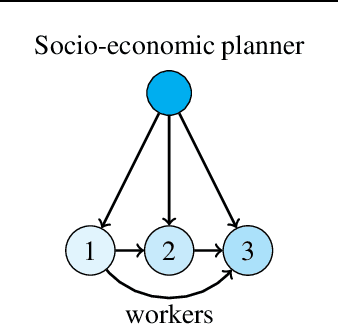
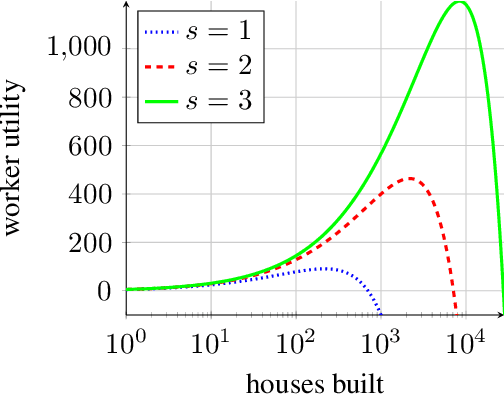
We consider a decentralized multiplayer game, played over $T$ rounds, with a leader-follower hierarchy described by a directed acyclic graph. For each round, the graph structure dictates the order of the players and how players observe the actions of one another. By the end of each round, all players receive a joint bandit-reward based on their joint action that is used to update the player strategies towards the goal of minimizing the joint pseudo-regret. We present a learning algorithm inspired by the single-player multi-armed bandit problem and show that it achieves sub-linear joint pseudo-regret in the number of rounds for both adversarial and stochastic bandit rewards. Furthermore, we quantify the cost incurred due to the decentralized nature of our problem compared to the centralized setting.

Model-Free Algorithm and Regret Analysis for MDPs with Long-Term Constraints

In the optimization of dynamical systems, the variables typically have constraints. Such problems can be modeled as a constrained Markov Decision Process (CMDP). This paper considers a model-free approach to the problem, where the transition probabilities are not known. In the presence of long-term (or average) constraints, the agent has to choose a policy that maximizes the long-term average reward as well as satisfy the average constraints in each episode. The key challenge with the long-term constraints is that the optimal policy is not deterministic in general, and thus standard Q-learning approaches cannot be directly used. This paper uses concepts from constrained optimization and Q-learning to propose an algorithm for CMDP with long-term constraints. For any $\gamma\in(0,\frac{1}{2})$, the proposed algorithm is shown to achieve $O(T^{1/2+\gamma})$ regret bound for the obtained reward and $O(T^{1-\gamma/2})$ regret bound for the constraint violation, where $T$ is the total number of steps. We note that these are the first results on regret analysis for MDP with long-term constraints, where the transition probabilities are not known apriori.

Model-Free Algorithm and Regret Analysis for MDPs with Peak Constraints

In the optimization of dynamic systems, the variables typically have constraints. Such problems can be modeled as a constrained Markov Decision Process (MDP). This paper considers a model-free approach to the problem, where the transition probabilities are not known. In the presence of peak constraints, the agent has to choose the policy to maximize the long-term average reward as well as satisfy the constraints at each time. We propose modifications to the standard Q-learning problem for unconstrained optimization to come up with an algorithm with peak constraints. The proposed algorithm is shown to achieve $O(T^{1/2+\gamma})$ regret bound for the obtained reward, and $O(T^{1-\gamma})$ regret bound for the constraint violation for any $\gamma \in(0,1/2)$ and time-horizon $T$. We note that these are the first results on regret analysis for constrained MDP, where the transition problems are not known apriori. We demonstrate the proposed algorithm on an energy harvesting problem where it outperforms state-of-the-art and performs close to the theoretical upper bound of the studied optimization problem.

Conditional Mutual information-based Contrastive Loss for Financial Time Series Forecasting

We present a method for financial time series forecasting using representation learning techniques. Recent progress on deep autoregressive models has shown their ability to capture long-term dependencies of the sequence data. However, the shortage of available financial data for training will make the deep models susceptible to the overfitting problem. In this paper, we propose a neural-network-powered conditional mutual information (CMI) estimator for learning representations for the forecasting task. Specifically, we first train an encoder to maximize the mutual information between the latent variables and the label information conditioned on the encoded observed variables. Then the features extracted from the trained encoder are used to learn a subsequent logistic regression model for predicting time series movements. Our proposed estimator transforms the CMI maximization problem to a classification problem whether two encoded representations are sampled from the same class or not. This is equivalent to perform pairwise comparisons of the training datapoints, and thus, improves the generalization ability of the deep autoregressive model. Empirical experiments indicate that our proposed method has the potential to advance the state-of-the-art performance.

Quantization-Based Regularization for Autoencoders

Autoencoders and their variations provide unsupervised models for learning low-dimensional representations for downstream tasks. Without proper regularization, autoencoder models are susceptible to the overfitting problem and the so-called posterior collapse phenomenon. In this paper, we introduce a quantization-based regularizer in the bottleneck stage of autoencoder models to learn meaningful latent representations. We combine both perspectives of Vector Quantized-Variational AutoEncoders (VQ-VAE) and classical denoising regularization schemes of neural networks. We interpret quantizers as regularizers that constrain latent representations while fostering a similarity mapping at the encoder. Before quantization, we impose noise on the latent variables and use a Bayesian estimator to optimize the quantizer-based representation. The introduced bottleneck Bayesian estimator outputs the posterior mean of the centroids to the decoder, and thus, is performing soft quantization of the latent variables. We show that our proposed regularization method results in improved latent representations for both supervised learning and clustering downstream tasks when compared to autoencoders using other bottleneck structures.

Reinforcement Learning of Markov Decision Processes with Peak Constraints

In this paper, we consider reinforcement learning of Markov Decision Processes (MDP) with peak constraints, where an agent chooses a policy to optimize an objective and at the same time satisfy additional constraints. The agent has to take actions based on the observed states, reward outputs, and constraint-outputs, without any knowledge about the dynamics, reward functions, and/or the knowledge of the constraint-functions. We introduce a game theoretic approach to construct reinforcement learning algorithms where the agent maximizes an unconstrained objective that depends on the simulated action of the minimizing opponent which acts on a finite set of actions and the output data of the constraint functions (rewards). We show that the policies obtained from maximin Q-learning converge to the optimal policies. To the best of our knowledge, this is the first time learning algorithms guarantee convergence to optimal stationary policies for the MDP problem with peak constraints for both discounted and expected average rewards.