Decentralized Online Bandit Optimization on Directed Graphs with Regret Bounds
Paper and Code
Jan 27, 2023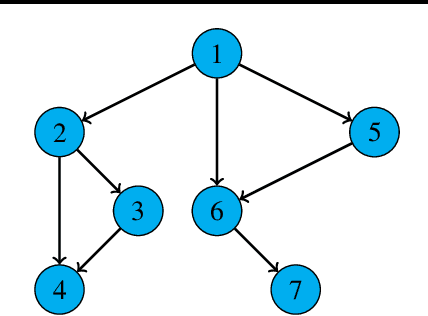
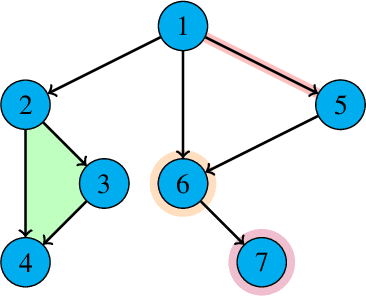
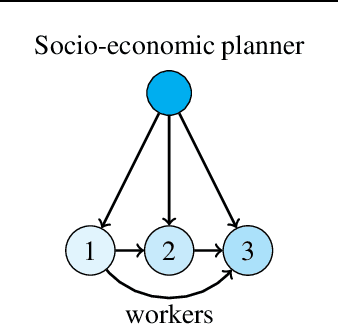
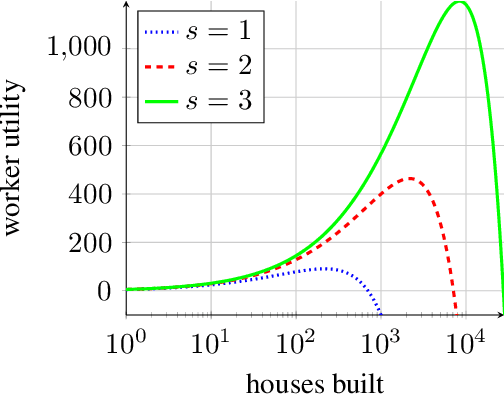
We consider a decentralized multiplayer game, played over $T$ rounds, with a leader-follower hierarchy described by a directed acyclic graph. For each round, the graph structure dictates the order of the players and how players observe the actions of one another. By the end of each round, all players receive a joint bandit-reward based on their joint action that is used to update the player strategies towards the goal of minimizing the joint pseudo-regret. We present a learning algorithm inspired by the single-player multi-armed bandit problem and show that it achieves sub-linear joint pseudo-regret in the number of rounds for both adversarial and stochastic bandit rewards. Furthermore, we quantify the cost incurred due to the decentralized nature of our problem compared to the centralized setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge