Evidential uncertainties on rich labels for active learning

Recent research in active learning, and more precisely in uncertainty sampling, has focused on the decomposition of model uncertainty into reducible and irreducible uncertainties. In this paper, we propose to simplify the computational phase and remove the dependence on observations, but more importantly to take into account the uncertainty already present in the labels, \emph{i.e.} the uncertainty of the oracles. Two strategies are proposed, sampling by Klir uncertainty, which addresses the exploration-exploitation problem, and sampling by evidential epistemic uncertainty, which extends the reducible uncertainty to the evidential framework, both using the theory of belief functions.

Estimation of the qualification and behavior of a contributor and aggregation of his answers in a crowdsourcing context

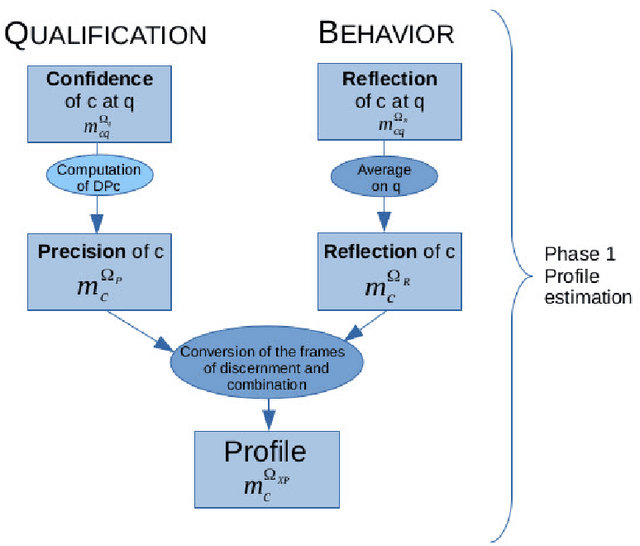
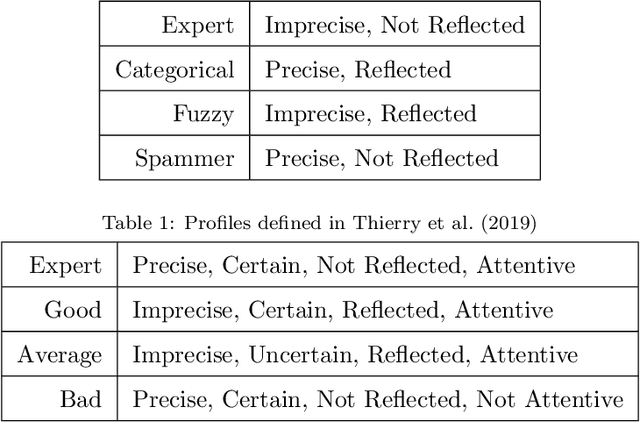
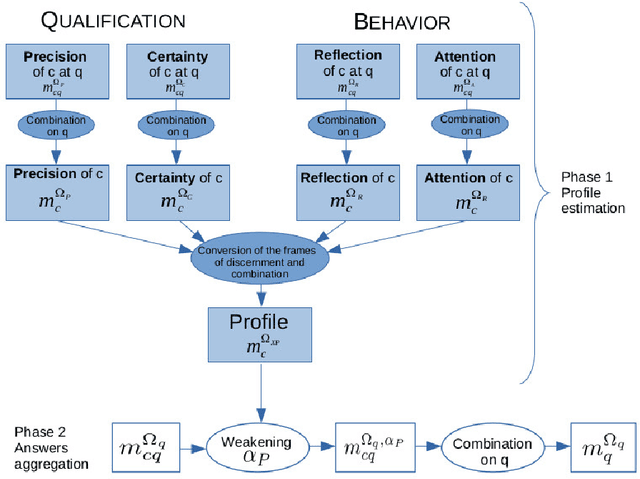
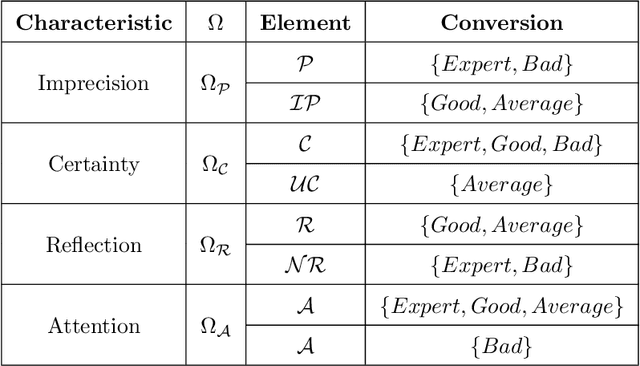
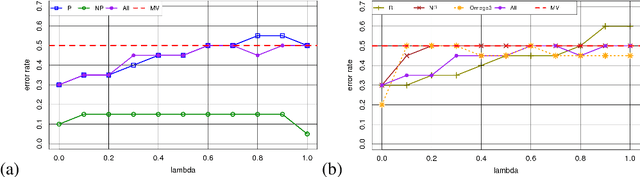
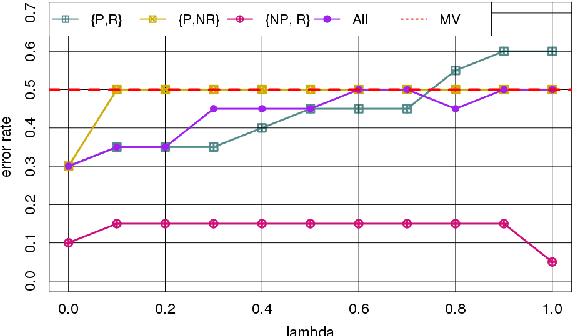
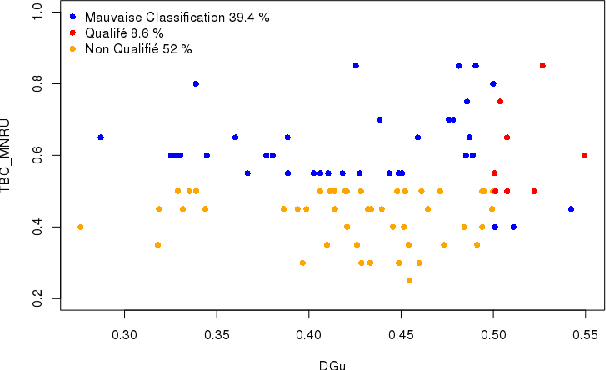
Crowdsourcing is the outsourcing of tasks to a crowd of contributors on a dedicated platform. The crowd on these platforms is very diversified and includes various profiles of contributors which generates data of uneven quality. However, majority voting, which is the aggregating method commonly used in platforms, gives equal weight to each contribution. To overcome this problem, we propose a method, MONITOR, which estimates the contributor's profile and aggregates the collected data by taking into account their possible imperfections thanks to the theory of belief functions. To do so, MONITOR starts by estimating the profile of the contributor through his qualification for the task and his behavior.Crowdsourcing campaigns have been carried out to collect the necessary data to test MONITOR on real data in order to compare it to existing approaches. The results of the experiments show that thanks to the use of the MONITOR method, we obtain a better rate of correct answer after aggregation of the contributions compared to the majority voting. Our contributions in this article are for the first time the proposal of a model that takes into account both the qualification of the contributor and his behavior in the estimation of his profile. For the second one, the weakening and the aggregation of the answers according to the estimated profiles.

Belief functions on ordered frames of discernment

Most questionnaires offer ordered responses whose order is poorly studied via belief functions. In this paper, we study the consequences of a frame of discernment consisting of ordered elements on belief functions. This leads us to redefine the power space and the union of ordered elements for the disjunctive combination. We also study distances on ordered elements and their use. In particular, from a membership function, we redefine the cardinality of the intersection of ordered elements, considering them fuzzy.

Modelisation de l'incertitude et de l'imprecision de donnees de crowdsourcing : MONITOR

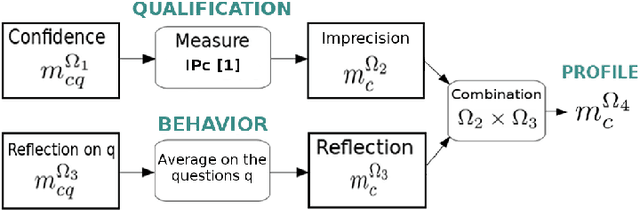
Crowdsourcing is defined as the outsourcing of tasks to a crowd of contributors. The crowd is very diverse on these platforms and includes malicious contributors attracted by the remuneration of tasks and not conscientiously performing them. It is essential to identify these contributors in order to avoid considering their responses. As not all contributors have the same aptitude for a task, it seems appropriate to give weight to their answers according to their qualifications. This paper, published at the ICTAI 2019 conference, proposes a method, MONITOR, for estimating the profile of the contributor and aggregating the responses using belief function theory.

Evidential positive opinion influence measures for viral marketing

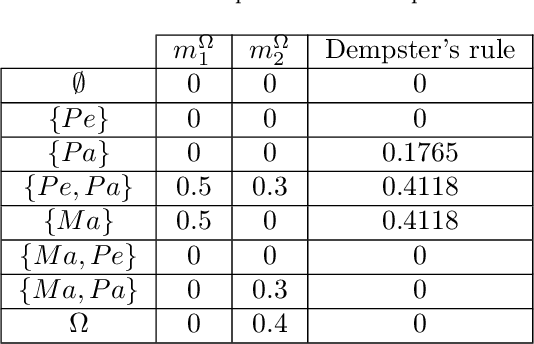
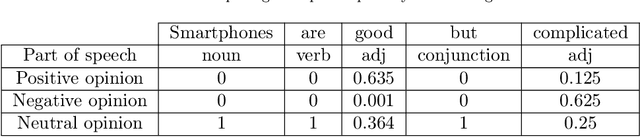
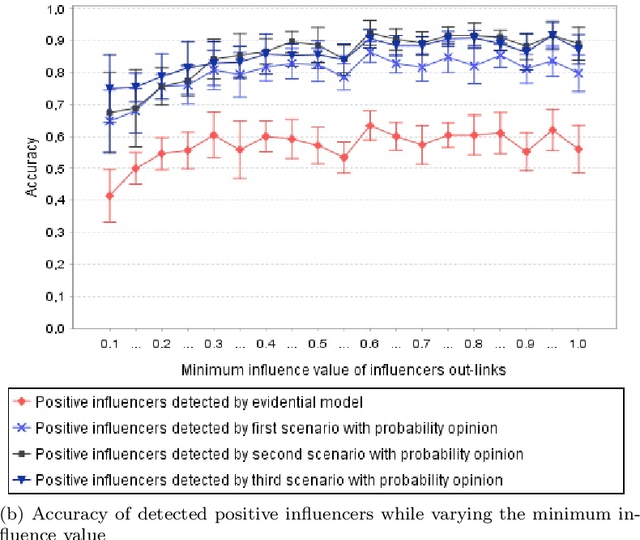
The Viral Marketing is a relatively new form of marketing that exploits social networks to promote a brand, a product, etc. The idea behind it is to find a set of influencers on the network that can trigger a large cascade of propagation and adoptions. In this paper, we will introduce an evidential opinion-based influence maximization model for viral marketing. Besides, our approach tackles three opinions based scenarios for viral marketing in the real world. The first scenario concerns influencers who have a positive opinion about the product. The second scenario deals with influencers who have a positive opinion about the product and produce effects on users who also have a positive opinion. The third scenario involves influence users who have a positive opinion about the product and produce effects on the negative opinion of other users concerning the product in question. Next, we proposed six influence measures, two for each scenario. We also use an influence maximization model that the set of detected influencers for each scenario. Finally, we show the performance of the proposed model with each influence measure through some experiments conducted on a generated dataset and a real world dataset collected from Twitter.

Contributors profile modelization in crowdsourcing platforms

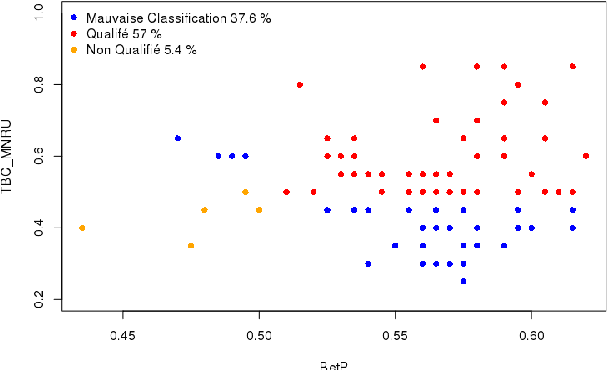
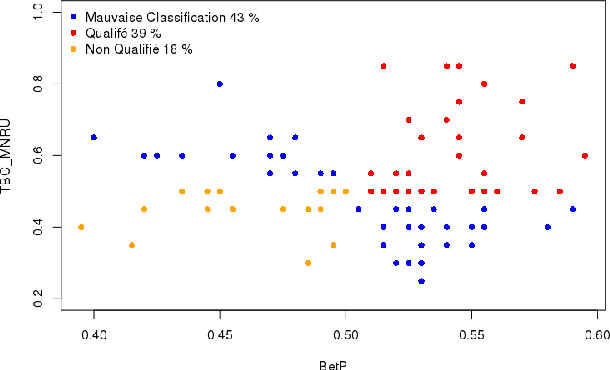
The crowdsourcing consists in the externalisation of tasks to a crowd of people remunerated to execute this ones. The crowd, usually diversified, can include users without qualification and/or motivation for the tasks. In this paper we will introduce a new method of user expertise modelization in the crowdsourcing platforms based on the theory of belief functions in order to identify serious and qualificated users.

A belief combination rule for a large number of sources

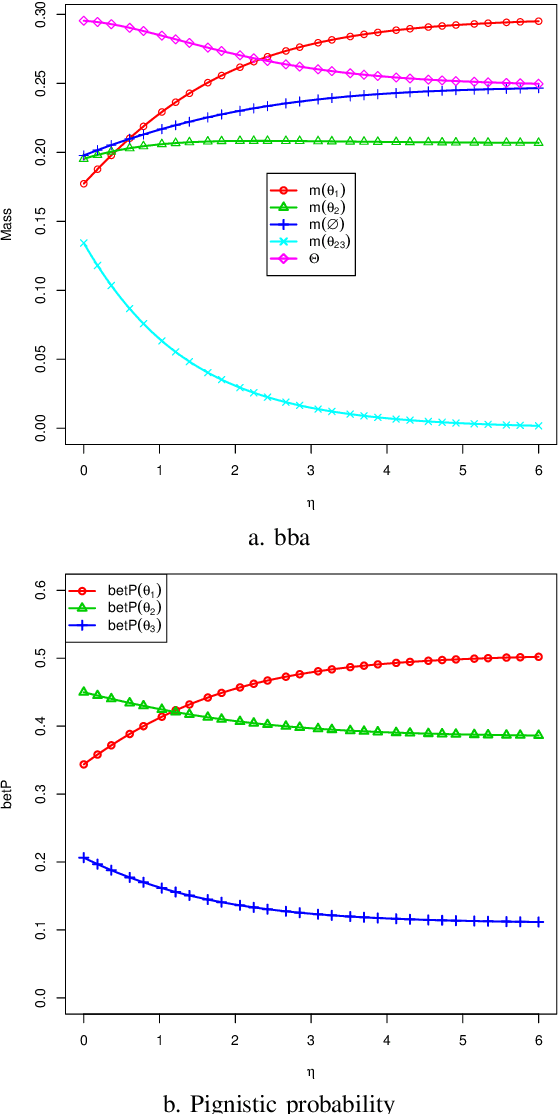
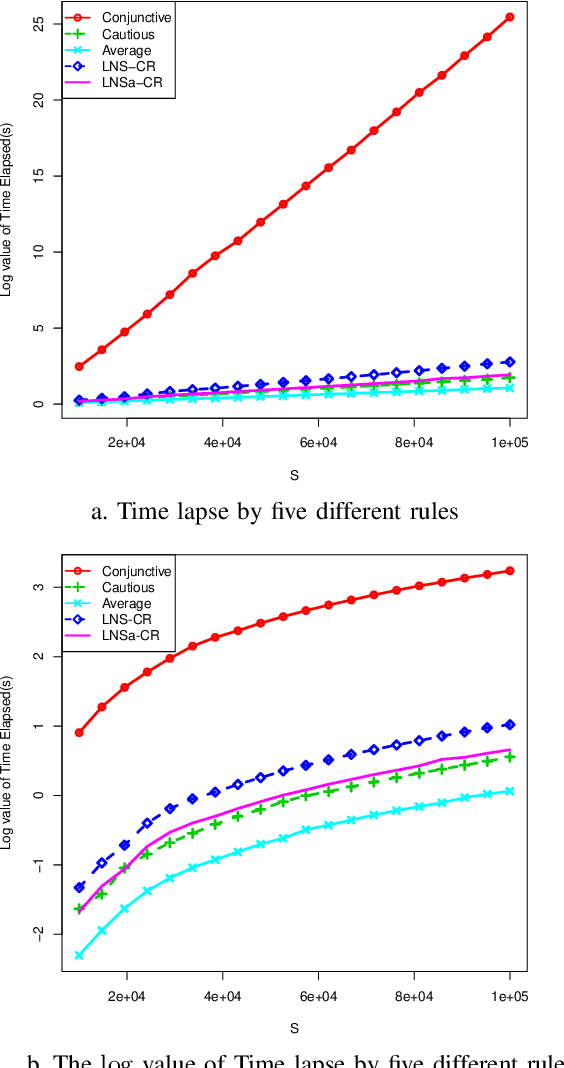
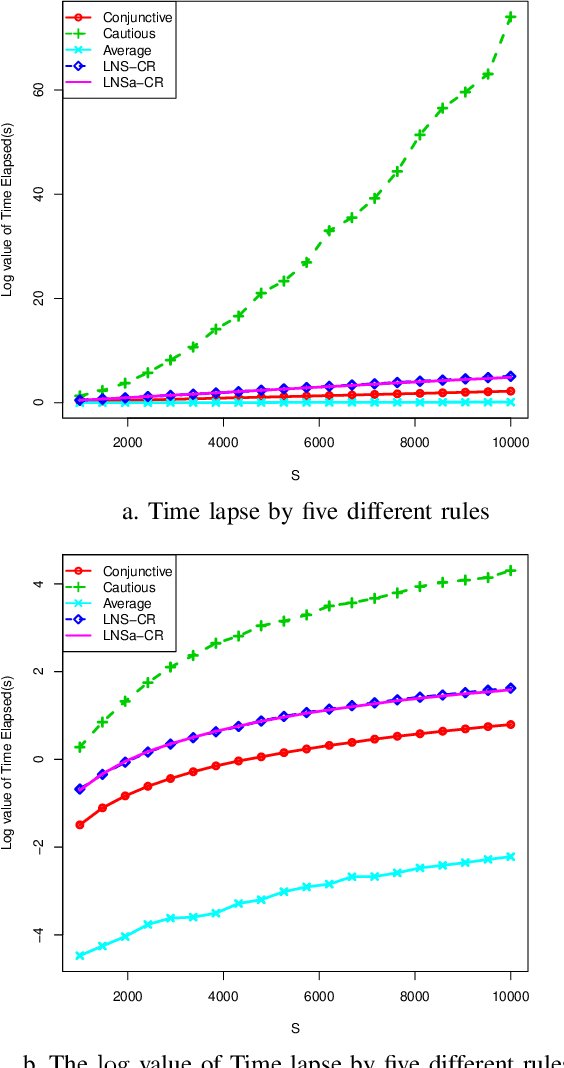
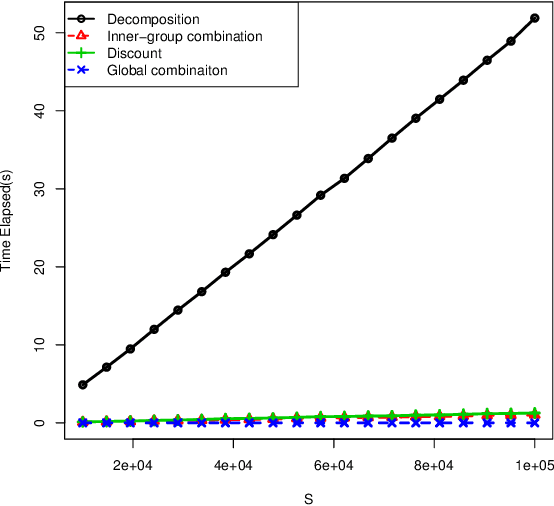
The theory of belief functions is widely used for data from multiple sources. Different evidence combination rules have been proposed in this framework according to the properties of the sources to combine. However, most of these combination rules are not efficient when there are a large number of sources. This is due to either the complexity or the existence of an absorbing element such as the total conflict mass function for the conjunctive based rules when applied on unreliable evidence. In this paper, based on the assumption that the majority of sources are reliable, a combination rule for a large number of sources is proposed using a simple idea: the more common ideas the sources share, the more reliable these sources are supposed to be. This rule is adaptable for aggregating a large number of sources which may not all be reliable. It will keep the spirit of the conjunctive rule to reinforce the belief on the focal elements with which the sources are in agreement. The mass on the emptyset will be kept as an indicator of the conflict. The proposed rule, called LNS-CR (Conjunctive combinationRule for a Large Number of Sources), is evaluated on synthetic mass functions. The experimental results verify that the rule can be effectively used to combine a large number of mass functions and to elicit the major opinion.

Evidential community detection based on density peaks

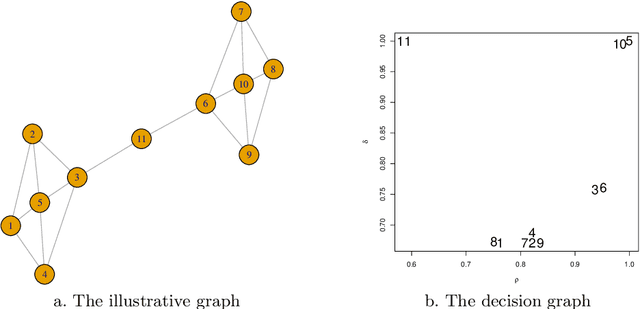
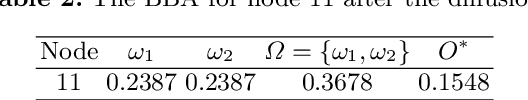
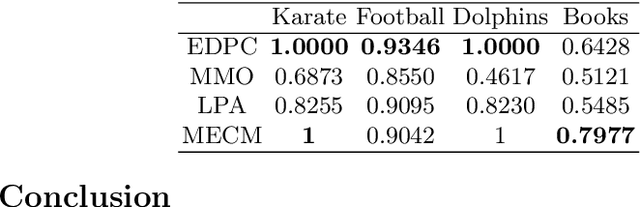
Credal partitions in the framework of belief functions can give us a better understanding of the analyzed data set. In order to find credal community structure in graph data sets, in this paper, we propose a novel evidential community detection algorithm based on density peaks (EDPC). Two new metrics, the local density $\rho$ and the minimum dissimi-larity $\delta$, are first defined for each node in the graph. Then the nodes with both higher $\rho$ and $\delta$ values are identified as community centers. Finally, the remaing nodes are assigned with corresponding community labels through a simple two-step evidential label propagation strategy. The membership of each node is described in the form of basic belief assignments , which can well express the uncertainty included in the community structure of the graph. The experiments demonstrate the effectiveness of the proposed method on real-world networks.

Independence of Sources in Social Networks

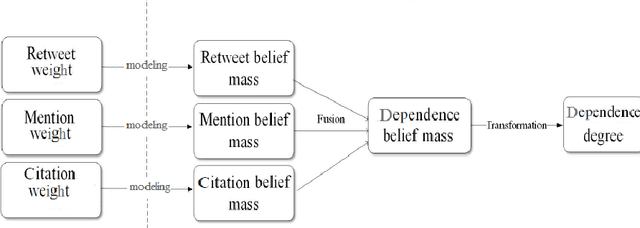
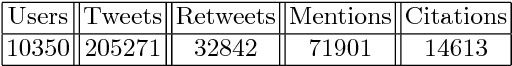
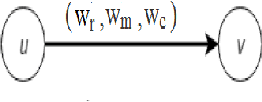
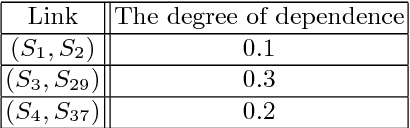
Online social networks are more and more studied. The links between users of a social network are important and have to be well qualified in order to detect communities and find influencers for example. In this paper, we present an approach based on the theory of belief functions to estimate the degrees of cognitive independence between users in a social network. We experiment the proposed method on a large amount of data gathered from the Twitter social network.

Conflict management in information fusion with belief functions

In Information fusion, the conflict is an important concept. Indeed, combining several imperfect experts or sources allows conflict. In the theory of belief functions, this notion has been discussed a lot. The mass appearing on the empty set during the conjunctive combination rule is generally considered as conflict, but that is not really a conflict. Some measures of conflict have been proposed and some approaches have been proposed in order to manage this conflict or to decide with conflicting mass functions. We recall in this chapter some of them and we propose a discussion to consider the conflict in information fusion with the theory of belief functions.