Mouna Chebbah
LARODEC
Independence of Sources in Social Networks
Jun 26, 2018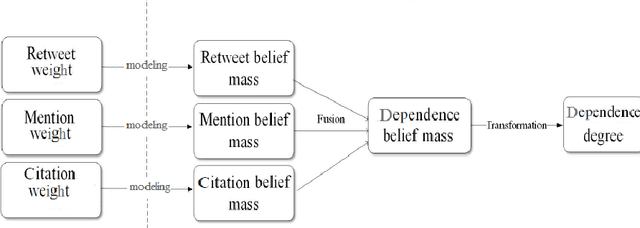
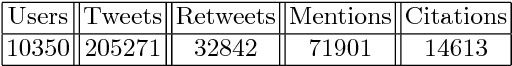
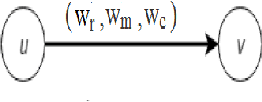
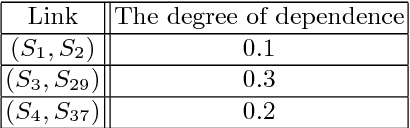
Abstract:Online social networks are more and more studied. The links between users of a social network are important and have to be well qualified in order to detect communities and find influencers for example. In this paper, we present an approach based on the theory of belief functions to estimate the degrees of cognitive independence between users in a social network. We experiment the proposed method on a large amount of data gathered from the Twitter social network.
Combining partially independent belief functions
Mar 17, 2015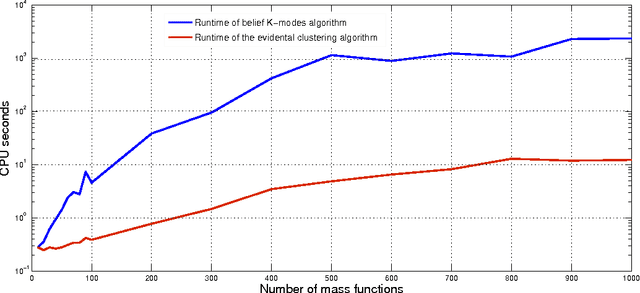
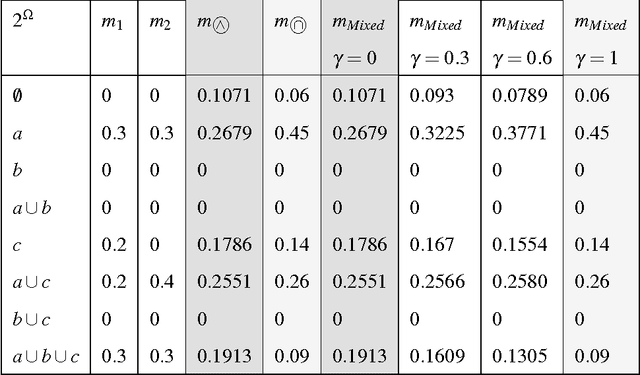
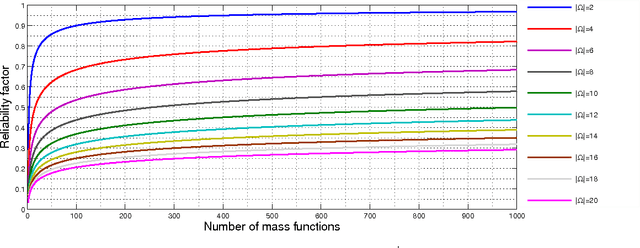

Abstract:The theory of belief functions manages uncertainty and also proposes a set of combination rules to aggregate opinions of several sources. Some combination rules mix evidential information where sources are independent; other rules are suited to combine evidential information held by dependent sources. In this paper we have two main contributions: First we suggest a method to quantify sources' degree of independence that may guide the choice of the more appropriate set of combination rules. Second, we propose a new combination rule that takes consideration of sources' degree of independence. The proposed method is illustrated on generated mass functions.
Second-Order Belief Hidden Markov Models
Jan 22, 2015
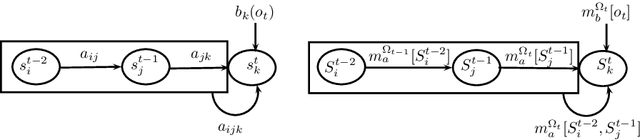
Abstract:Hidden Markov Models (HMMs) are learning methods for pattern recognition. The probabilistic HMMs have been one of the most used techniques based on the Bayesian model. First-order probabilistic HMMs were adapted to the theory of belief functions such that Bayesian probabilities were replaced with mass functions. In this paper, we present a second-order Hidden Markov Model using belief functions. Previous works in belief HMMs have been focused on the first-order HMMs. We extend them to the second-order model.
Consid{é}rant la d{é}pendance dans la th{é}orie des fonctions de croyance
Jan 20, 2015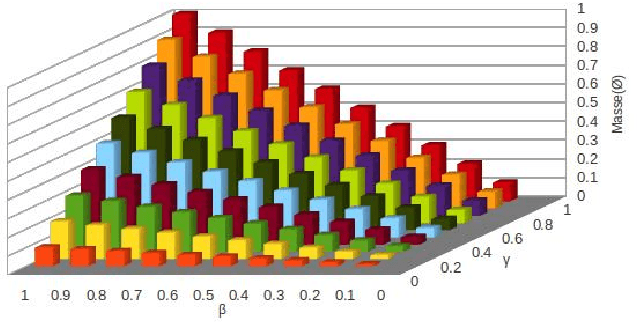
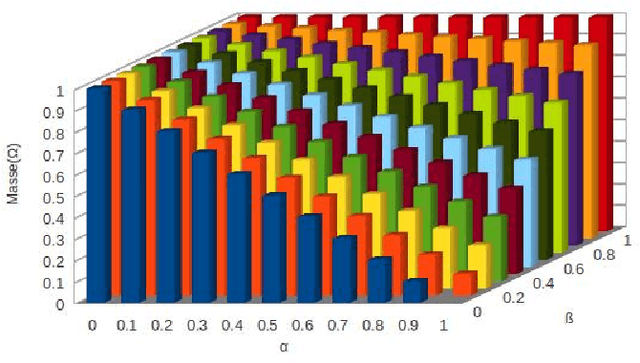
Abstract:In this paper, we propose to learn sources independence in order to choose the appropriate type of combination rules when aggregating their beliefs. Some combination rules are used with the assumption of their sources independence whereas others combine beliefs of dependent sources. Therefore, the choice of the combination rule depends on the independence of sources involved in the combination. In this paper, we propose also a measure of independence, positive and negative dependence to integrate in mass functions before the combinaision with the independence assumption.
* in French
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge