A belief combination rule for a large number of sources

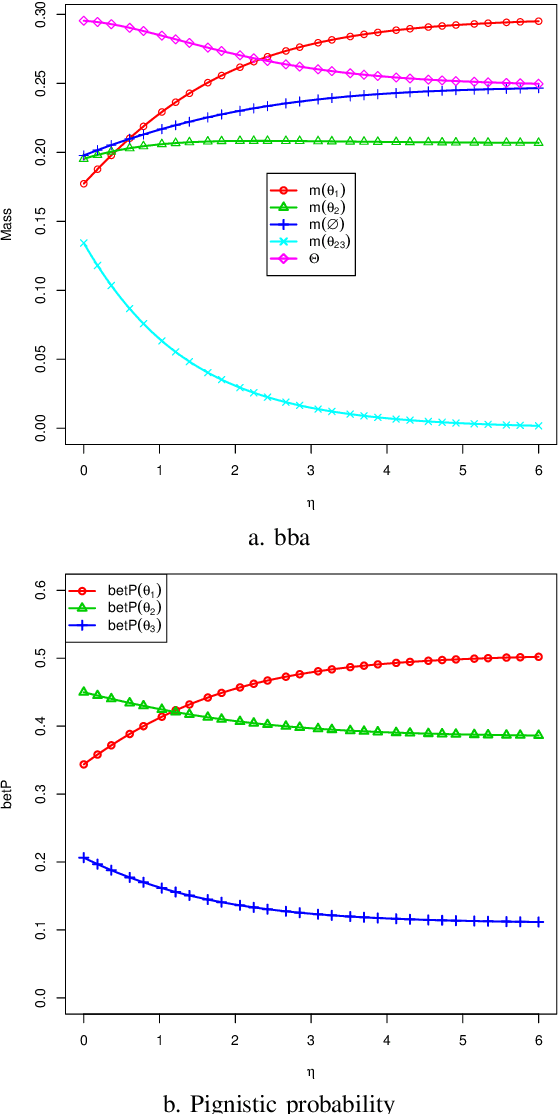
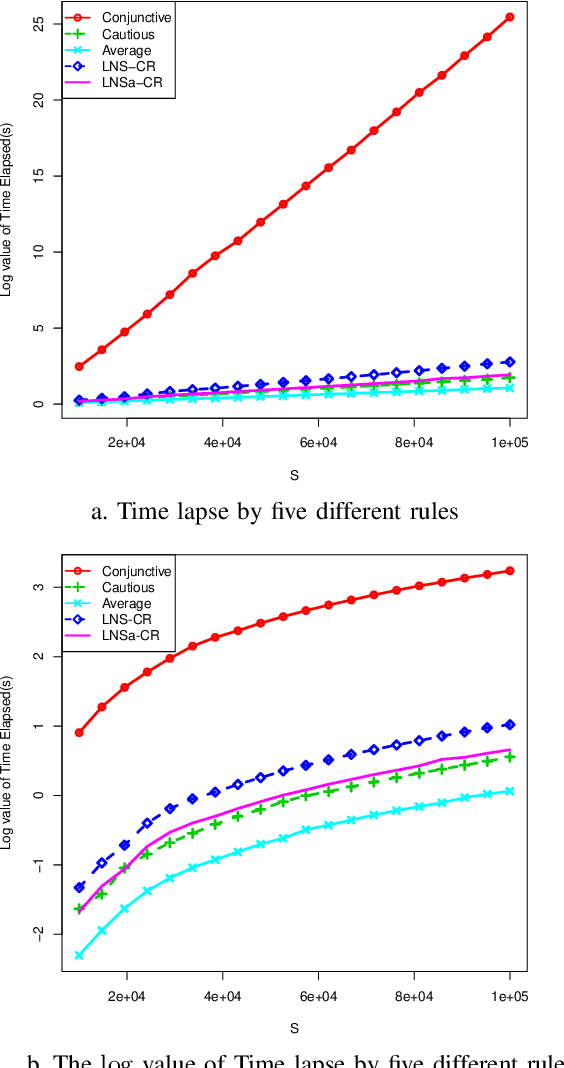
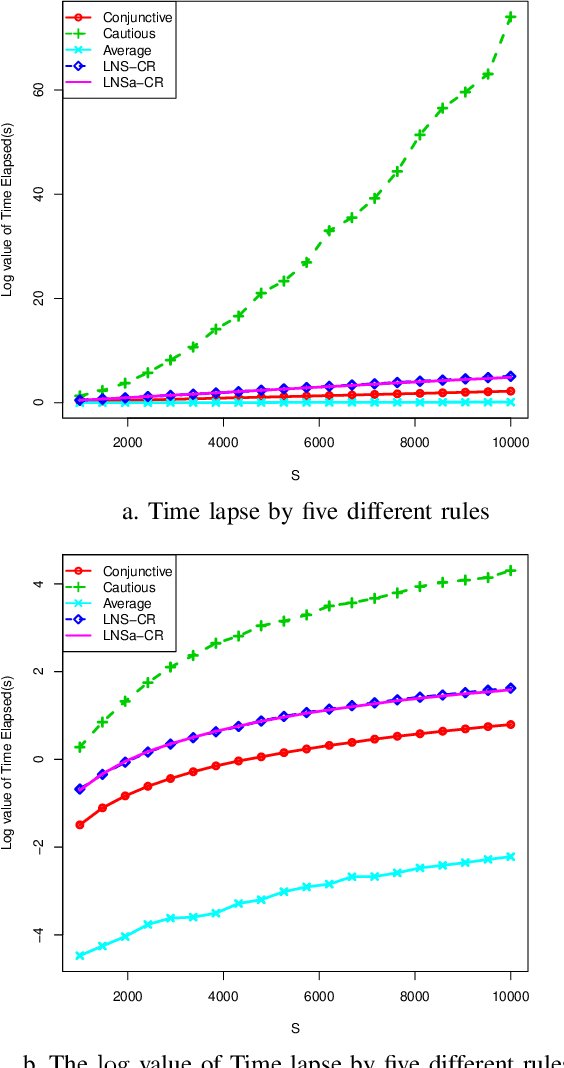
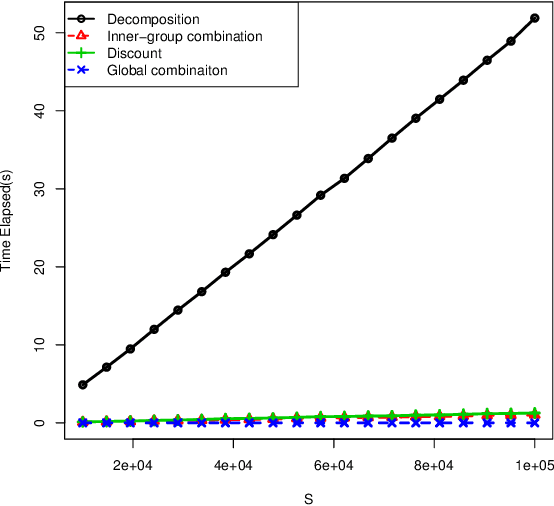
The theory of belief functions is widely used for data from multiple sources. Different evidence combination rules have been proposed in this framework according to the properties of the sources to combine. However, most of these combination rules are not efficient when there are a large number of sources. This is due to either the complexity or the existence of an absorbing element such as the total conflict mass function for the conjunctive based rules when applied on unreliable evidence. In this paper, based on the assumption that the majority of sources are reliable, a combination rule for a large number of sources is proposed using a simple idea: the more common ideas the sources share, the more reliable these sources are supposed to be. This rule is adaptable for aggregating a large number of sources which may not all be reliable. It will keep the spirit of the conjunctive rule to reinforce the belief on the focal elements with which the sources are in agreement. The mass on the emptyset will be kept as an indicator of the conflict. The proposed rule, called LNS-CR (Conjunctive combinationRule for a Large Number of Sources), is evaluated on synthetic mass functions. The experimental results verify that the rule can be effectively used to combine a large number of mass functions and to elicit the major opinion.

Evidential community detection based on density peaks

Credal partitions in the framework of belief functions can give us a better understanding of the analyzed data set. In order to find credal community structure in graph data sets, in this paper, we propose a novel evidential community detection algorithm based on density peaks (EDPC). Two new metrics, the local density $\rho$ and the minimum dissimi-larity $\delta$, are first defined for each node in the graph. Then the nodes with both higher $\rho$ and $\delta$ values are identified as community centers. Finally, the remaing nodes are assigned with corresponding community labels through a simple two-step evidential label propagation strategy. The membership of each node is described in the form of basic belief assignments , which can well express the uncertainty included in the community structure of the graph. The experiments demonstrate the effectiveness of the proposed method on real-world networks.

The Advantage of Evidential Attributes in Social Networks

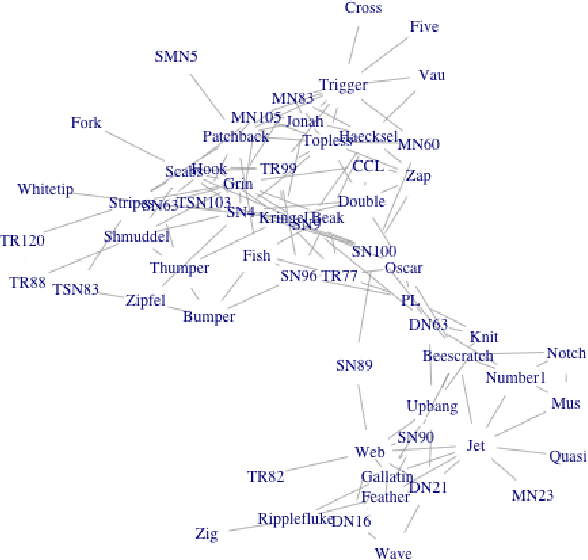
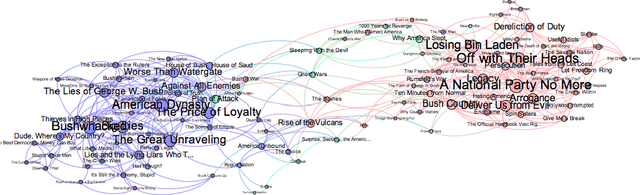
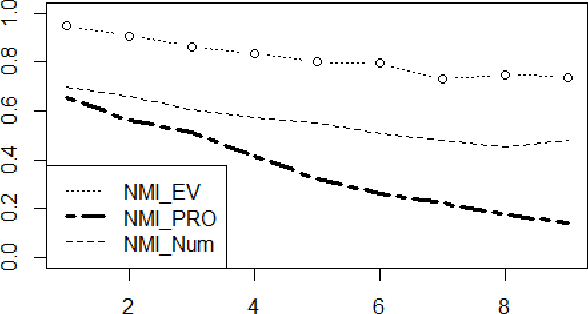
Nowadays, there are many approaches designed for the task of detecting communities in social networks. Among them, some methods only consider the topological graph structure, while others take use of both the graph structure and the node attributes. In real-world networks, there are many uncertain and noisy attributes in the graph. In this paper, we will present how we detect communities in graphs with uncertain attributes in the first step. The numerical, probabilistic as well as evidential attributes are generated according to the graph structure. In the second step, some noise will be added to the attributes. We perform experiments on graphs with different types of attributes and compare the detection results in terms of the Normalized Mutual Information (NMI) values. The experimental results show that the clustering with evidential attributes gives better results comparing to those with probabilistic and numerical attributes. This illustrates the advantages of evidential attributes.

Evidence combination for a large number of sources

The theory of belief functions is an effective tool to deal with the multiple uncertain information. In recent years, many evidence combination rules have been proposed in this framework, such as the conjunctive rule, the cautious rule, the PCR (Proportional Conflict Redistribution) rules and so on. These rules can be adopted for different types of sources. However, most of these rules are not applicable when the number of sources is large. This is due to either the complexity or the existence of an absorbing element (such as the total conflict mass function for the conjunctive-based rules when applied on unreliable evidence). In this paper, based on the assumption that the majority of sources are reliable, a combination rule for a large number of sources, named LNS (stands for Large Number of Sources), is proposed on the basis of a simple idea: the more common ideas one source shares with others, the morereliable the source is. This rule is adaptable for aggregating a large number of sources among which some are unreliable. It will keep the spirit of the conjunctive rule to reinforce the belief on the focal elements with which the sources are in agreement. The mass on the empty set will be kept as an indicator of the conflict. Moreover, it can be used to elicit the major opinion among the experts. The experimental results on synthetic mass functionsverify that the rule can be effectively used to combine a large number of mass functions and to elicit the major opinion.

Semi-supervised evidential label propagation algorithm for graph data

In the task of community detection, there often exists some useful prior information. In this paper, a Semi-supervised clustering approach using a new Evidential Label Propagation strategy (SELP) is proposed to incorporate the domain knowledge into the community detection model. The main advantage of SELP is that it can take limited supervised knowledge to guide the detection process. The prior information of community labels is expressed in the form of mass functions initially. Then a new evidential label propagation rule is adopted to propagate the labels from labeled data to unlabeled ones. The outliers can be identified to be in a special class. The experimental results demonstrate the effectiveness of SELP.

Evidential Label Propagation Algorithm for Graphs

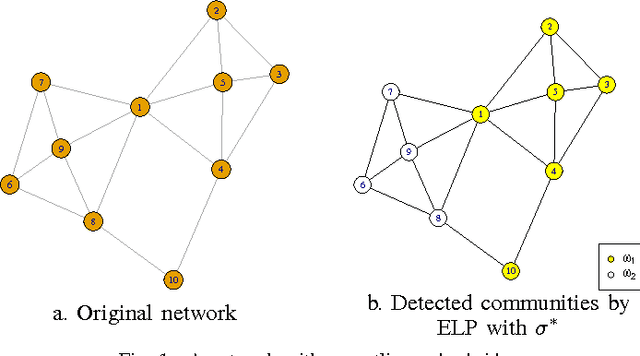
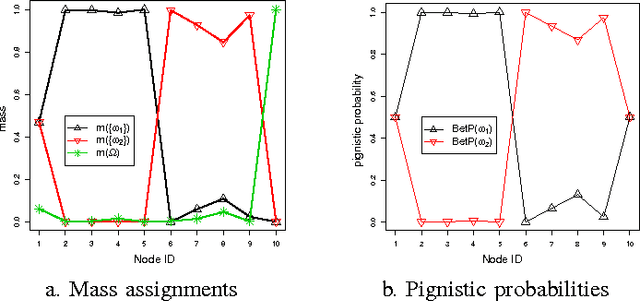
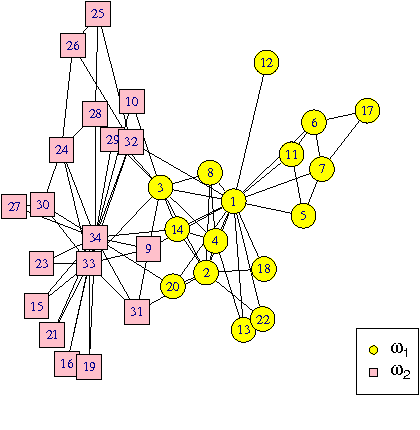
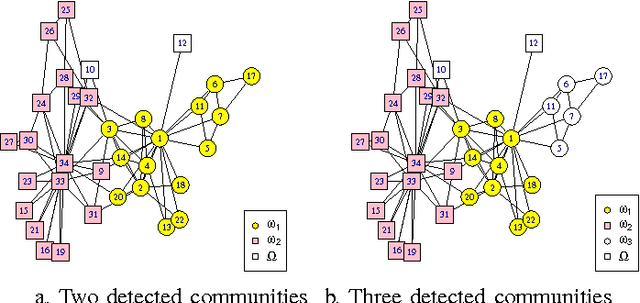
Community detection has attracted considerable attention crossing many areas as it can be used for discovering the structure and features of complex networks. With the increasing size of social networks in real world, community detection approaches should be fast and accurate. The Label Propagation Algorithm (LPA) is known to be one of the near-linear solutions and benefits of easy implementation, thus it forms a good basis for efficient community detection methods. In this paper, we extend the update rule and propagation criterion of LPA in the framework of belief functions. A new community detection approach, called Evidential Label Propagation (ELP), is proposed as an enhanced version of conventional LPA. The node influence is first defined to guide the propagation process. The plausibility is used to determine the domain label of each node. The update order of nodes is discussed to improve the robustness of the method. ELP algorithm will converge after the domain labels of all the nodes become unchanged. The mass assignments are calculated finally as memberships of nodes. The overlapping nodes and outliers can be detected simultaneously through the proposed method. The experimental results demonstrate the effectiveness of ELP.

The belief noisy-or model applied to network reliability analysis

One difficulty faced in knowledge engineering for Bayesian Network (BN) is the quan-tification step where the Conditional Probability Tables (CPTs) are determined. The number of parameters included in CPTs increases exponentially with the number of parent variables. The most common solution is the application of the so-called canonical gates. The Noisy-OR (NOR) gate, which takes advantage of the independence of causal interactions, provides a logarithmic reduction of the number of parameters required to specify a CPT. In this paper, an extension of NOR model based on the theory of belief functions, named Belief Noisy-OR (BNOR), is proposed. BNOR is capable of dealing with both aleatory and epistemic uncertainty of the network. Compared with NOR, more rich information which is of great value for making decisions can be got when the available knowledge is uncertain. Specially, when there is no epistemic uncertainty, BNOR degrades into NOR. Additionally, different structures of BNOR are presented in this paper in order to meet various needs of engineers. The application of BNOR model on the reliability evaluation problem of networked systems demonstrates its effectiveness.

ECMdd: Evidential c-medoids clustering with multiple prototypes

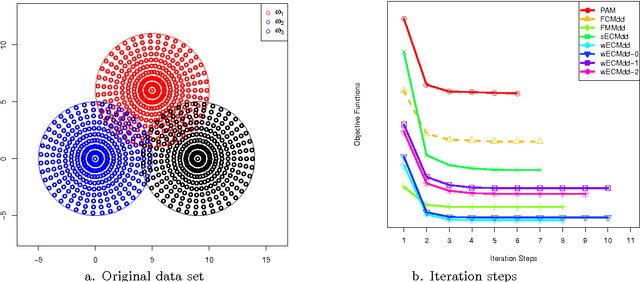
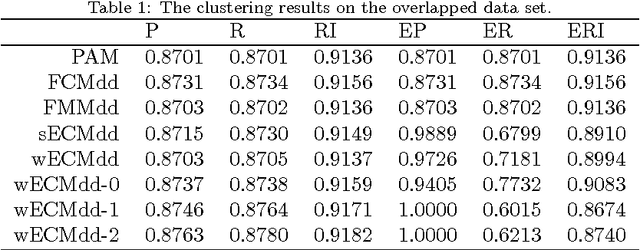
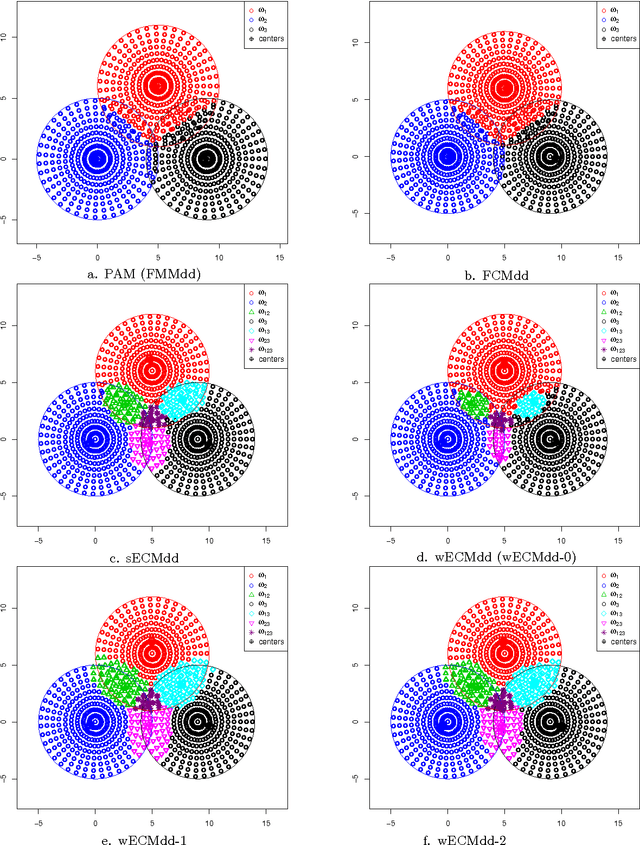
In this work, a new prototype-based clustering method named Evidential C-Medoids (ECMdd), which belongs to the family of medoid-based clustering for proximity data, is proposed as an extension of Fuzzy C-Medoids (FCMdd) on the theoretical framework of belief functions. In the application of FCMdd and original ECMdd, a single medoid (prototype), which is supposed to belong to the object set, is utilized to represent one class. For the sake of clarity, this kind of ECMdd using a single medoid is denoted by sECMdd. In real clustering applications, using only one pattern to capture or interpret a class may not adequately model different types of group structure and hence limits the clustering performance. In order to address this problem, a variation of ECMdd using multiple weighted medoids, denoted by wECMdd, is presented. Unlike sECMdd, in wECMdd objects in each cluster carry various weights describing their degree of representativeness for that class. This mechanism enables each class to be represented by more than one object. Experimental results in synthetic and real data sets clearly demonstrate the superiority of sECMdd and wECMdd. Moreover, the clustering results by wECMdd can provide richer information for the inner structure of the detected classes with the help of prototype weights.

Evidential relational clustering using medoids

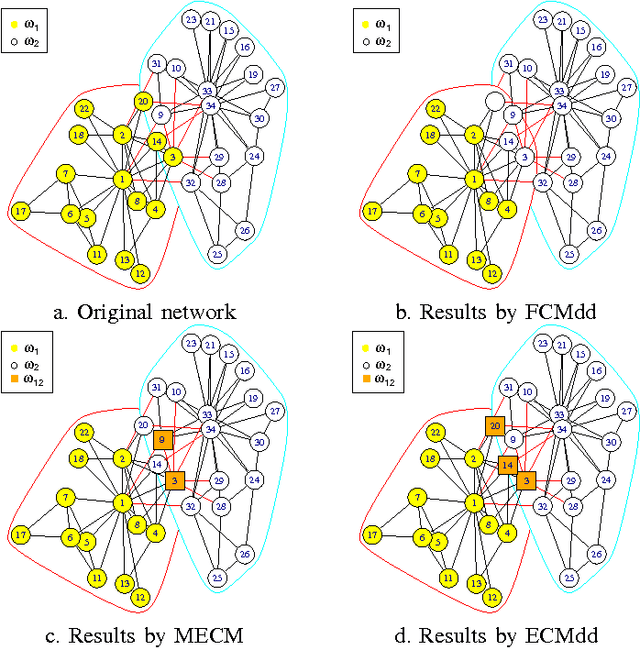
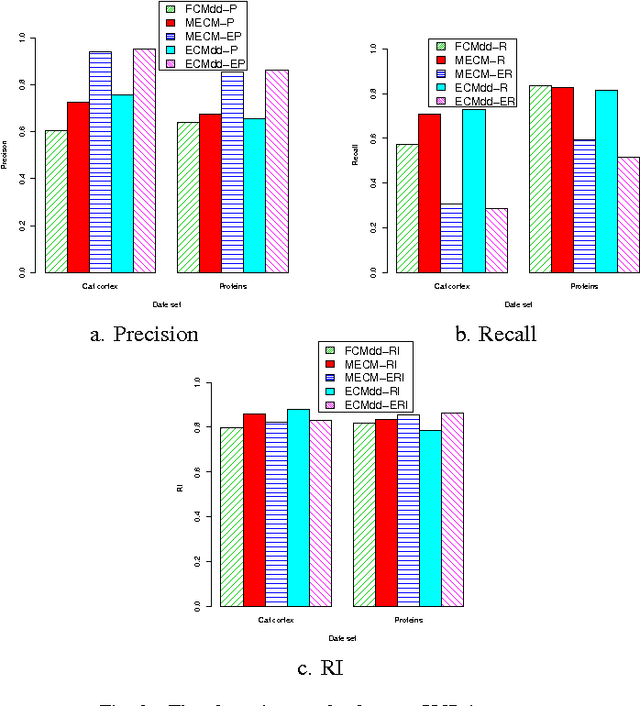
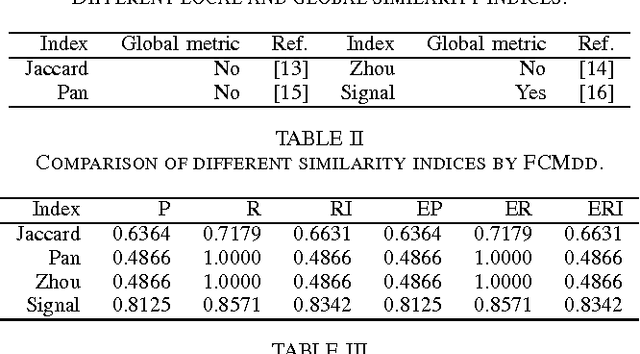
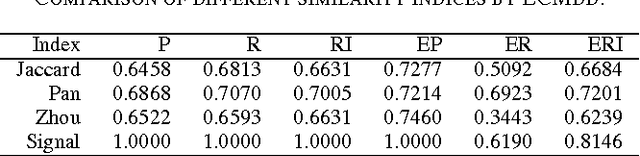
In real clustering applications, proximity data, in which only pairwise similarities or dissimilarities are known, is more general than object data, in which each pattern is described explicitly by a list of attributes. Medoid-based clustering algorithms, which assume the prototypes of classes are objects, are of great value for partitioning relational data sets. In this paper a new prototype-based clustering method, named Evidential C-Medoids (ECMdd), which is an extension of Fuzzy C-Medoids (FCMdd) on the theoretical framework of belief functions is proposed. In ECMdd, medoids are utilized as the prototypes to represent the detected classes, including specific classes and imprecise classes. Specific classes are for the data which are distinctly far from the prototypes of other classes, while imprecise classes accept the objects that may be close to the prototypes of more than one class. This soft decision mechanism could make the clustering results more cautious and reduce the misclassification rates. Experiments in synthetic and real data sets are used to illustrate the performance of ECMdd. The results show that ECMdd could capture well the uncertainty in the internal data structure. Moreover, it is more robust to the initializations compared with FCMdd.

Belief Hierarchical Clustering

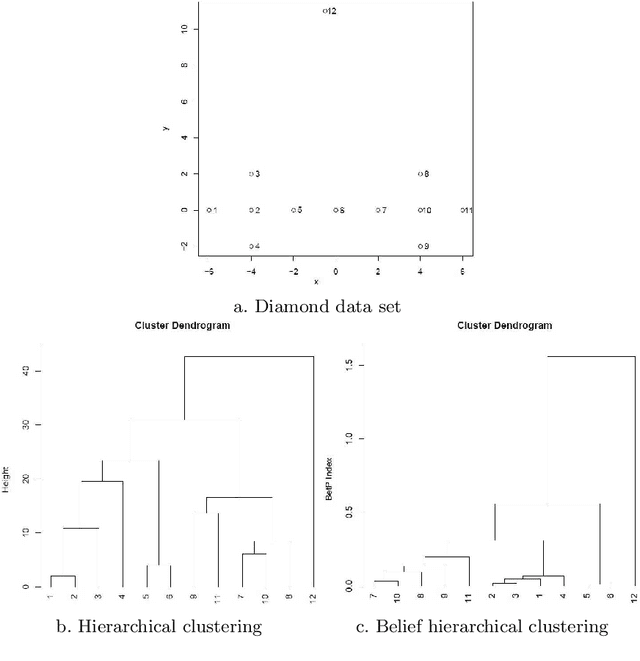
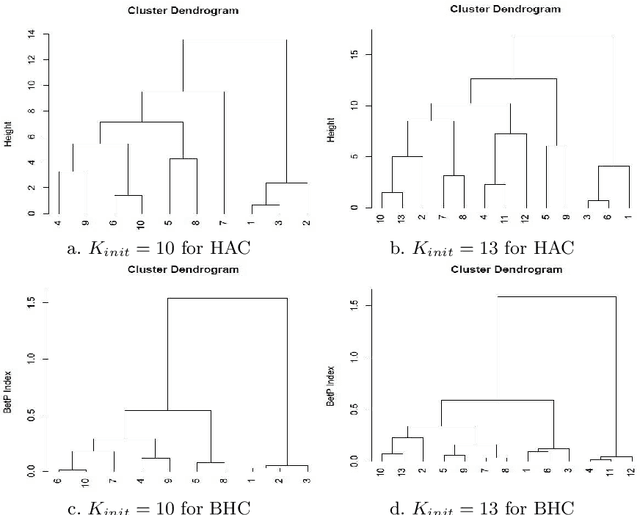
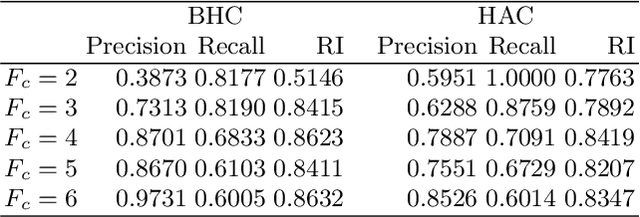
In the data mining field many clustering methods have been proposed, yet standard versions do not take into account uncertain databases. This paper deals with a new approach to cluster uncertain data by using a hierarchical clustering defined within the belief function framework. The main objective of the belief hierarchical clustering is to allow an object to belong to one or several clusters. To each belonging, a degree of belief is associated, and clusters are combined based on the pignistic properties. Experiments with real uncertain data show that our proposed method can be considered as a propitious tool.