Zhun-Ga Liu
Palaiseau
Evidential Label Propagation Algorithm for Graphs
Jun 13, 2016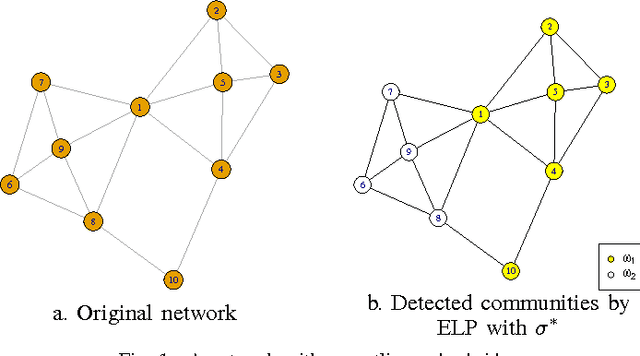
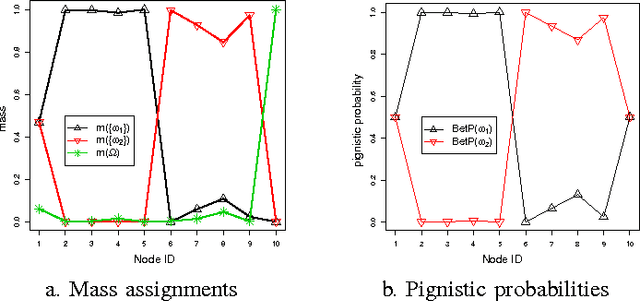
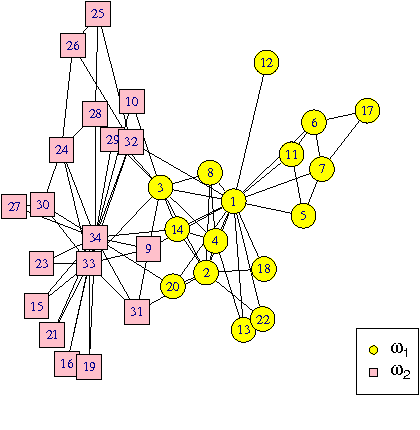
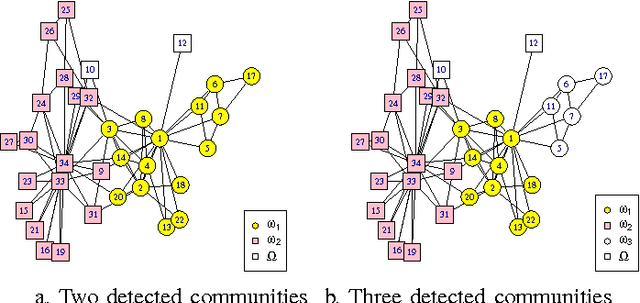
Abstract:Community detection has attracted considerable attention crossing many areas as it can be used for discovering the structure and features of complex networks. With the increasing size of social networks in real world, community detection approaches should be fast and accurate. The Label Propagation Algorithm (LPA) is known to be one of the near-linear solutions and benefits of easy implementation, thus it forms a good basis for efficient community detection methods. In this paper, we extend the update rule and propagation criterion of LPA in the framework of belief functions. A new community detection approach, called Evidential Label Propagation (ELP), is proposed as an enhanced version of conventional LPA. The node influence is first defined to guide the propagation process. The plausibility is used to determine the domain label of each node. The update order of nodes is discussed to improve the robustness of the method. ELP algorithm will converge after the domain labels of all the nodes become unchanged. The mass assignments are calculated finally as memberships of nodes. The overlapping nodes and outliers can be detected simultaneously through the proposed method. The experimental results demonstrate the effectiveness of ELP.
ECMdd: Evidential c-medoids clustering with multiple prototypes
Jun 03, 2016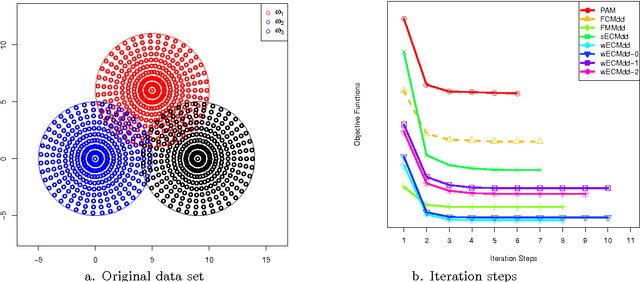
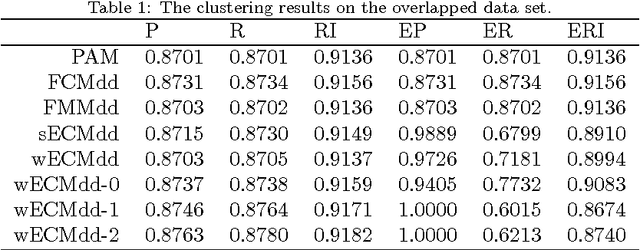
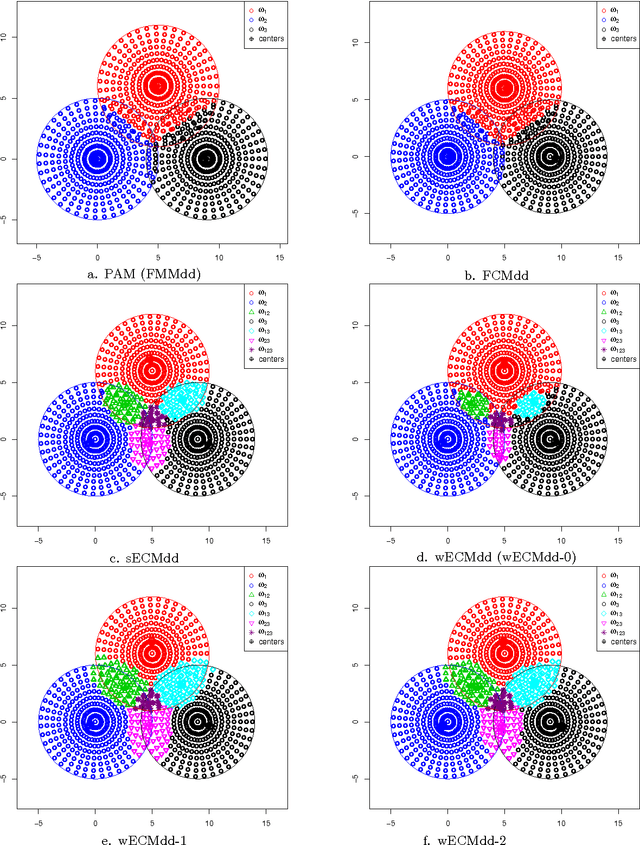

Abstract:In this work, a new prototype-based clustering method named Evidential C-Medoids (ECMdd), which belongs to the family of medoid-based clustering for proximity data, is proposed as an extension of Fuzzy C-Medoids (FCMdd) on the theoretical framework of belief functions. In the application of FCMdd and original ECMdd, a single medoid (prototype), which is supposed to belong to the object set, is utilized to represent one class. For the sake of clarity, this kind of ECMdd using a single medoid is denoted by sECMdd. In real clustering applications, using only one pattern to capture or interpret a class may not adequately model different types of group structure and hence limits the clustering performance. In order to address this problem, a variation of ECMdd using multiple weighted medoids, denoted by wECMdd, is presented. Unlike sECMdd, in wECMdd objects in each cluster carry various weights describing their degree of representativeness for that class. This mechanism enables each class to be represented by more than one object. Experimental results in synthetic and real data sets clearly demonstrate the superiority of sECMdd and wECMdd. Moreover, the clustering results by wECMdd can provide richer information for the inner structure of the detected classes with the help of prototype weights.
Adaptive imputation of missing values for incomplete pattern classification
Feb 08, 2016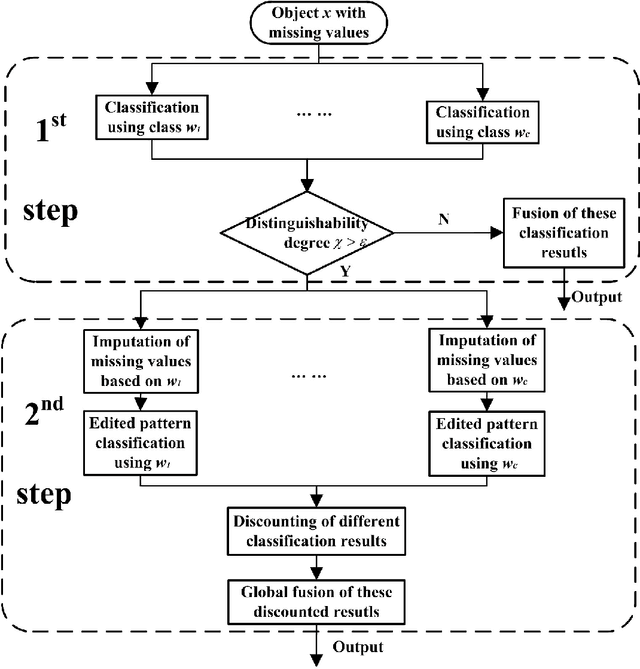
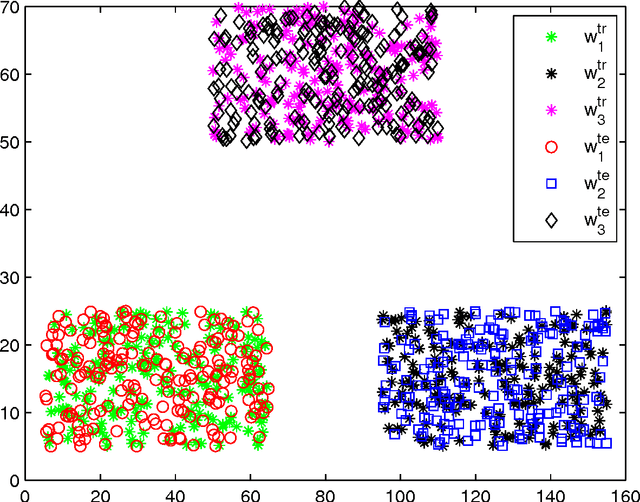

Abstract:In classification of incomplete pattern, the missing values can either play a crucial role in the class determination, or have only little influence (or eventually none) on the classification results according to the context. We propose a credal classification method for incomplete pattern with adaptive imputation of missing values based on belief function theory. At first, we try to classify the object (incomplete pattern) based only on the available attribute values. As underlying principle, we assume that the missing information is not crucial for the classification if a specific class for the object can be found using only the available information. In this case, the object is committed to this particular class. However, if the object cannot be classified without ambiguity, it means that the missing values play a main role for achieving an accurate classification. In this case, the missing values will be imputed based on the K-nearest neighbor (K-NN) and self-organizing map (SOM) techniques, and the edited pattern with the imputation is then classified. The (original or edited) pattern is respectively classified according to each training class, and the classification results represented by basic belief assignments are fused with proper combination rules for making the credal classification. The object is allowed to belong with different masses of belief to the specific classes and meta-classes (which are particular disjunctions of several single classes). The credal classification captures well the uncertainty and imprecision of classification, and reduces effectively the rate of misclassifications thanks to the introduction of meta-classes. The effectiveness of the proposed method with respect to other classical methods is demonstrated based on several experiments using artificial and real data sets.
Evidential relational clustering using medoids
Jul 15, 2015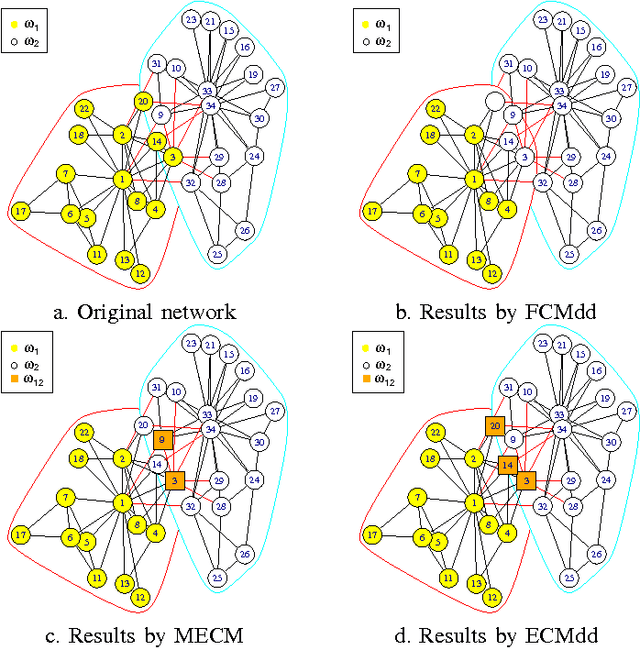
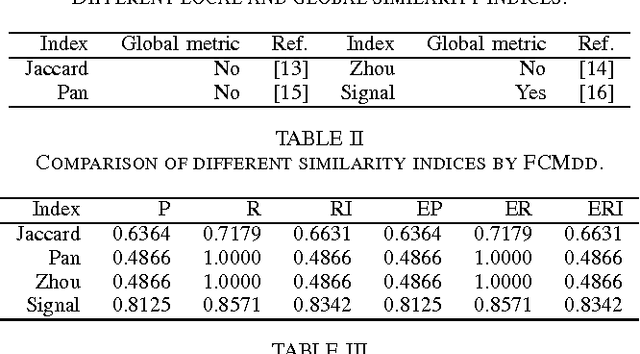
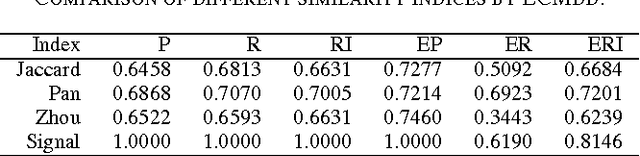
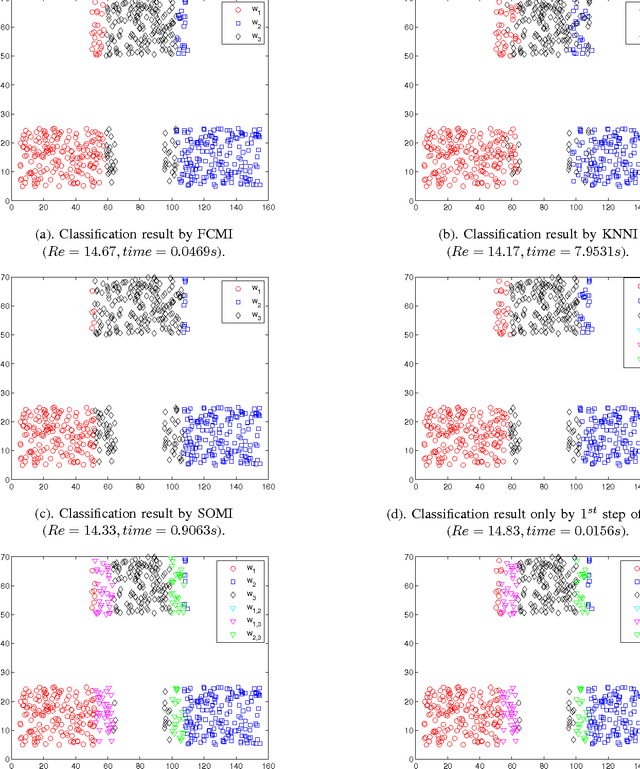
Abstract:In real clustering applications, proximity data, in which only pairwise similarities or dissimilarities are known, is more general than object data, in which each pattern is described explicitly by a list of attributes. Medoid-based clustering algorithms, which assume the prototypes of classes are objects, are of great value for partitioning relational data sets. In this paper a new prototype-based clustering method, named Evidential C-Medoids (ECMdd), which is an extension of Fuzzy C-Medoids (FCMdd) on the theoretical framework of belief functions is proposed. In ECMdd, medoids are utilized as the prototypes to represent the detected classes, including specific classes and imprecise classes. Specific classes are for the data which are distinctly far from the prototypes of other classes, while imprecise classes accept the objects that may be close to the prototypes of more than one class. This soft decision mechanism could make the clustering results more cautious and reduce the misclassification rates. Experiments in synthetic and real data sets are used to illustrate the performance of ECMdd. The results show that ECMdd could capture well the uncertainty in the internal data structure. Moreover, it is more robust to the initializations compared with FCMdd.
Median evidential c-means algorithm and its application to community detection
Jan 07, 2015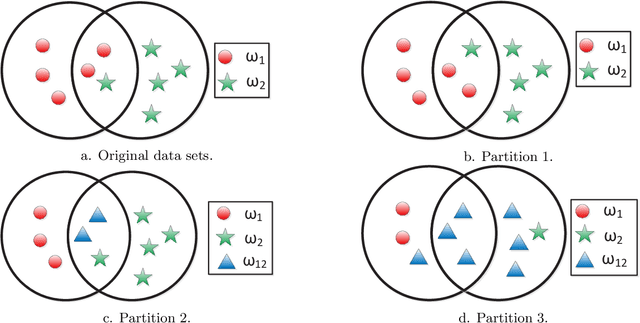

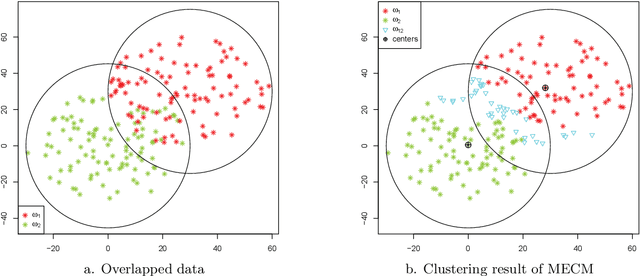
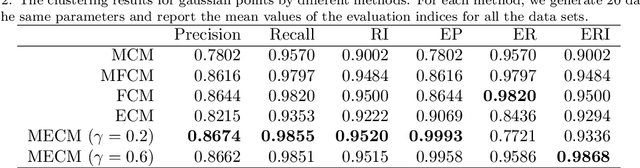
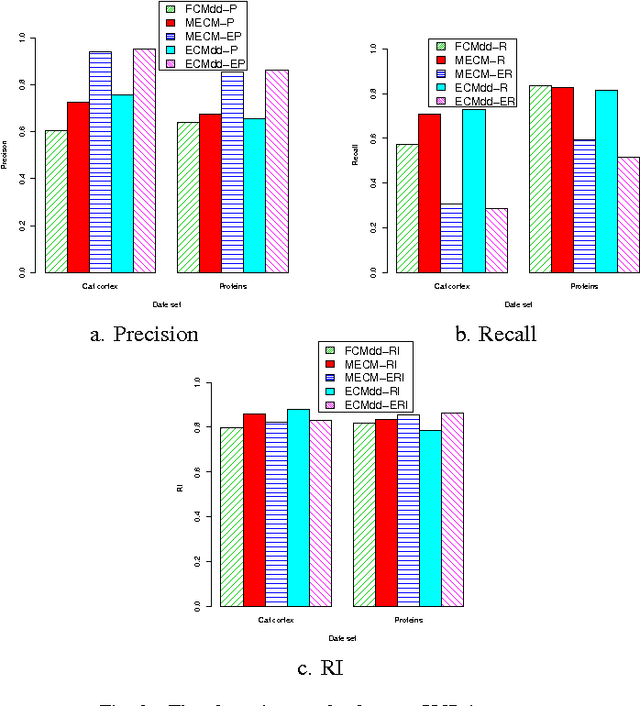
Abstract:Median clustering is of great value for partitioning relational data. In this paper, a new prototype-based clustering method, called Median Evidential C-Means (MECM), which is an extension of median c-means and median fuzzy c-means on the theoretical framework of belief functions is proposed. The median variant relaxes the restriction of a metric space embedding for the objects but constrains the prototypes to be in the original data set. Due to these properties, MECM could be applied to graph clustering problems. A community detection scheme for social networks based on MECM is investigated and the obtained credal partitions of graphs, which are more refined than crisp and fuzzy ones, enable us to have a better understanding of the graph structures. An initial prototype-selection scheme based on evidential semi-centrality is presented to avoid local premature convergence and an evidential modularity function is defined to choose the optimal number of communities. Finally, experiments in synthetic and real data sets illustrate the performance of MECM and show its difference to other methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge