Median evidential c-means algorithm and its application to community detection
Paper and Code
Jan 07, 2015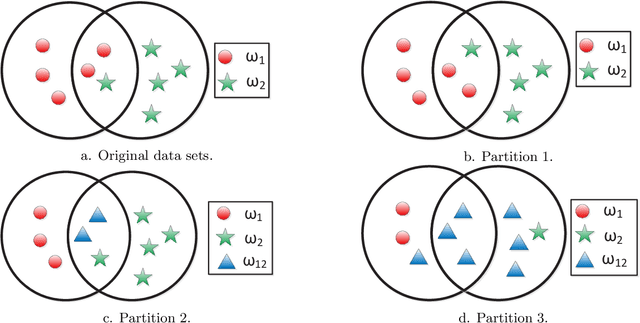

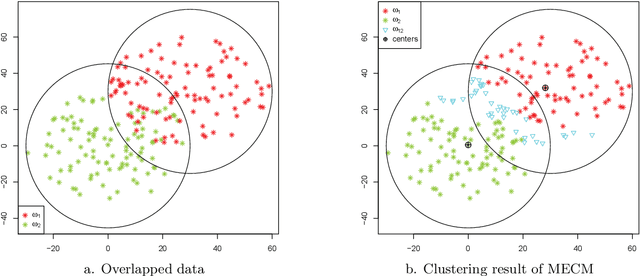
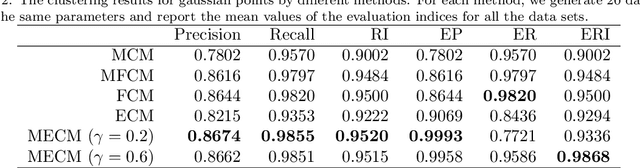
Median clustering is of great value for partitioning relational data. In this paper, a new prototype-based clustering method, called Median Evidential C-Means (MECM), which is an extension of median c-means and median fuzzy c-means on the theoretical framework of belief functions is proposed. The median variant relaxes the restriction of a metric space embedding for the objects but constrains the prototypes to be in the original data set. Due to these properties, MECM could be applied to graph clustering problems. A community detection scheme for social networks based on MECM is investigated and the obtained credal partitions of graphs, which are more refined than crisp and fuzzy ones, enable us to have a better understanding of the graph structures. An initial prototype-selection scheme based on evidential semi-centrality is presented to avoid local premature convergence and an evidential modularity function is defined to choose the optimal number of communities. Finally, experiments in synthetic and real data sets illustrate the performance of MECM and show its difference to other methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge