GraIP: A Benchmarking Framework For Neural Graph Inverse Problems

A wide range of graph learning tasks, such as structure discovery, temporal graph analysis, and combinatorial optimization, focus on inferring graph structures from data, rather than making predictions on given graphs. However, the respective methods to solve such problems are often developed in an isolated, task-specific manner and thus lack a unifying theoretical foundation. Here, we provide a stepping stone towards the formation of such a foundation and further development by introducing the Neural Graph Inverse Problem (GraIP) conceptual framework, which formalizes and reframes a broad class of graph learning tasks as inverse problems. Unlike discriminative approaches that directly predict target variables from given graph inputs, the GraIP paradigm addresses inverse problems, i.e., it relies on observational data and aims to recover the underlying graph structure by reversing the forward process, such as message passing or network dynamics, that produced the observed outputs. We demonstrate the versatility of GraIP across various graph learning tasks, including rewiring, causal discovery, and neural relational inference. We also propose benchmark datasets and metrics for each GraIP domain considered, and characterize and empirically evaluate existing baseline methods used to solve them. Overall, our unifying perspective bridges seemingly disparate applications and provides a principled approach to structural learning in constrained and combinatorial settings while encouraging cross-pollination of existing methods across graph inverse problems.

Preference-Based Gradient Estimation for ML-Based Approximate Combinatorial Optimization

Combinatorial optimization (CO) problems arise in a wide range of fields from medicine to logistics and manufacturing. While exact solutions are often not necessary, many applications require finding high-quality solutions quickly. For this purpose, we propose a data-driven approach to improve existing non-learned approximation algorithms for CO. We parameterize the approximation algorithm and train a graph neural network (GNN) to predict parameter values that lead to the best possible solutions. Our pipeline is trained end-to-end in a self-supervised fashion using gradient estimation, treating the approximation algorithm as a black box. We propose a novel gradient estimation scheme for this purpose, which we call preference-based gradient estimation. Our approach combines the benefits of the neural network and the non-learned approximation algorithm: The GNN leverages the information from the dataset to allow the approximation algorithm to find better solutions, while the approximation algorithm guarantees that the solution is feasible. We validate our approach on two well-known combinatorial optimization problems, the travelling salesman problem and the minimum k-cut problem, and show that our method is competitive with state of the art learned CO solvers.

Efficient Learning of Fast Inverse Kinematics with Collision Avoidance

Fast inverse kinematics (IK) is a central component in robotic motion planning. For complex robots, IK methods are often based on root search and non-linear optimization algorithms. These algorithms can be massively sped up using a neural network to predict a good initial guess, which can then be refined in a few numerical iterations. Besides previous work on learning-based IK, we present a learning approach for the fundamentally more complex problem of IK with collision avoidance. We do this in diverse and previously unseen environments. From a detailed analysis of the IK learning problem, we derive a network and unsupervised learning architecture that removes the need for a sample data generation step. Using the trained network's prediction as an initial guess for a two-stage Jacobian-based solver allows for fast and accurate computation of the collision-free IK. For the humanoid robot, Agile Justin (19 DoF), the collision-free IK is solved in less than 10 milliseconds (on a single CPU core) and with an accuracy of 10^-4 m and 10^-3 rad based on a high-resolution world model generated from the robot's integrated 3D sensor. Our method massively outperforms a random multi-start baseline in a benchmark with the 19 DoF humanoid and challenging 3D environments. It requires ten times less training time than a supervised training method while achieving comparable results.

Deep Learning for 2D and 3D Rotatable Data: An Overview of Methods

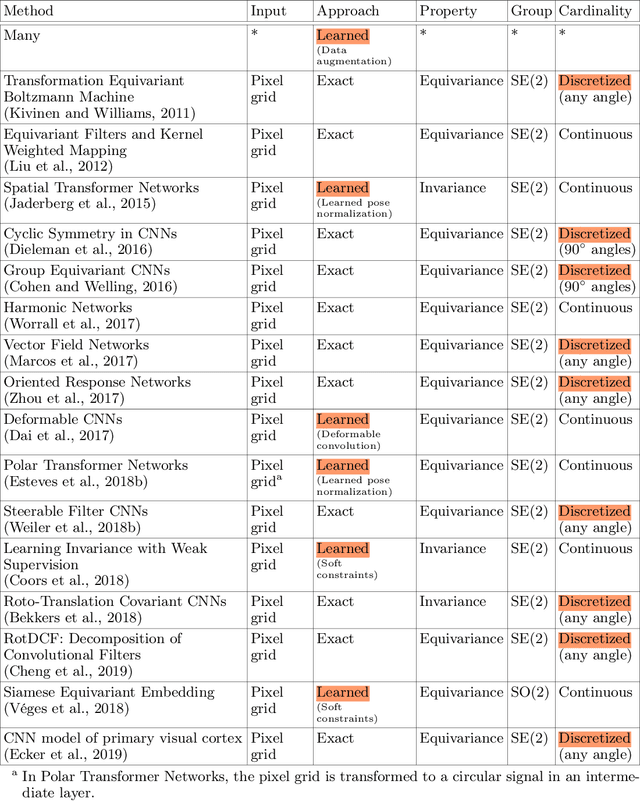
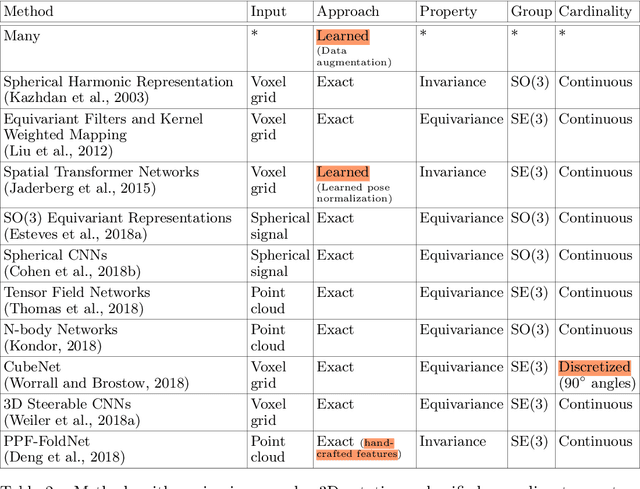
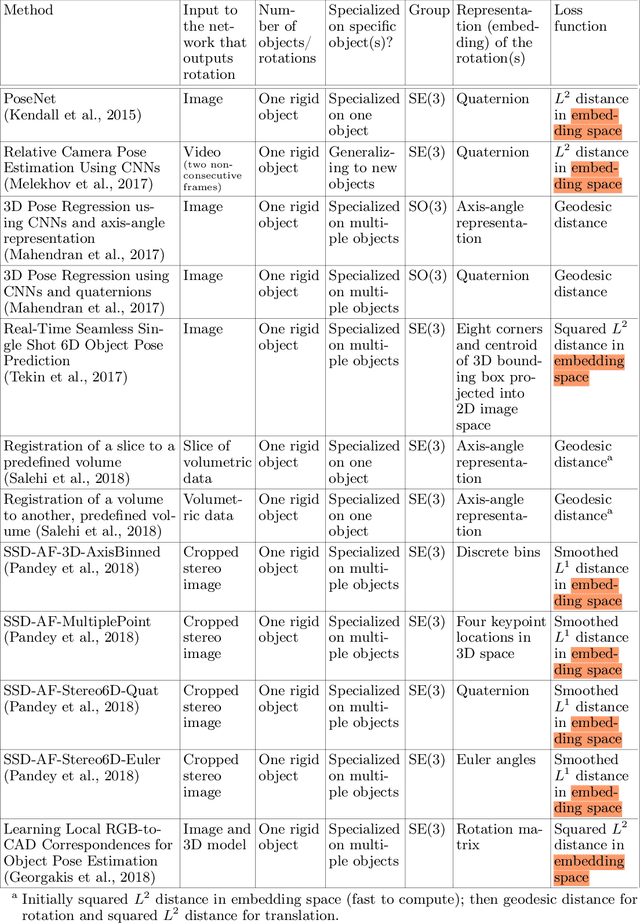
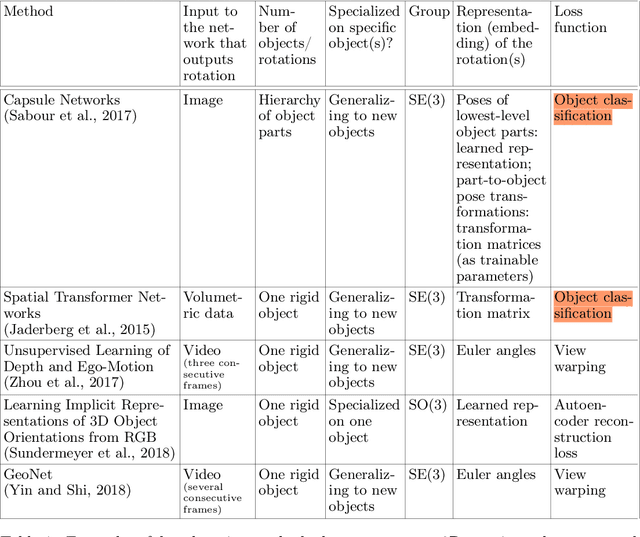
One of the reasons for the success of convolutional networks is their equivariance/invariance under translations. However, rotatable data such as molecules, living cells, everyday objects, or galaxies require processing with equivariance/invariance under rotations in cases where the rotation of the coordinate system does not affect the meaning of the data (e.g. object classification). On the other hand, estimation/processing of rotations is necessary in cases where rotations are important (e.g. motion estimation). There has been recent progress in methods and theory in all these regards. Here we provide an overview of existing methods, both for 2D and 3D rotations (and translations), and identify commonalities and links between them, in the hope that our insights will be useful for choosing and perfecting the methods.