Deep Learning for 2D and 3D Rotatable Data: An Overview of Methods

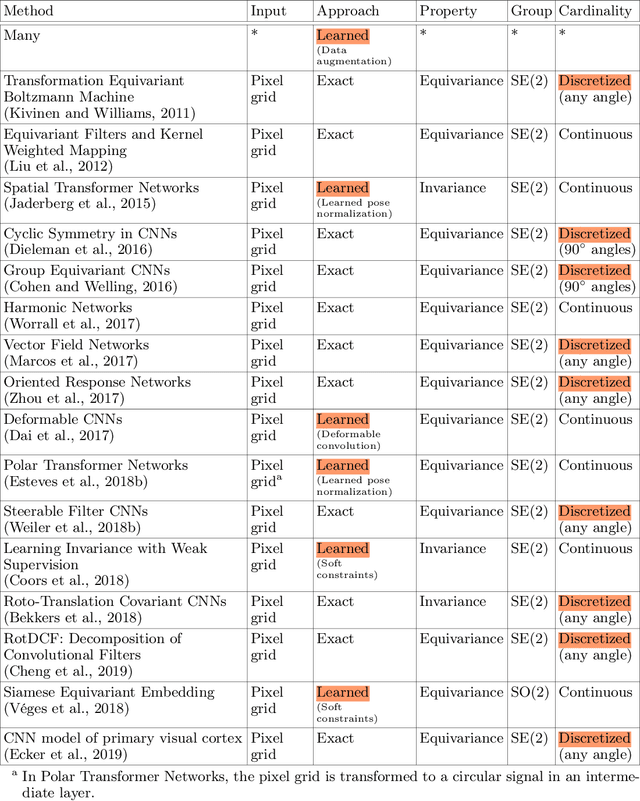
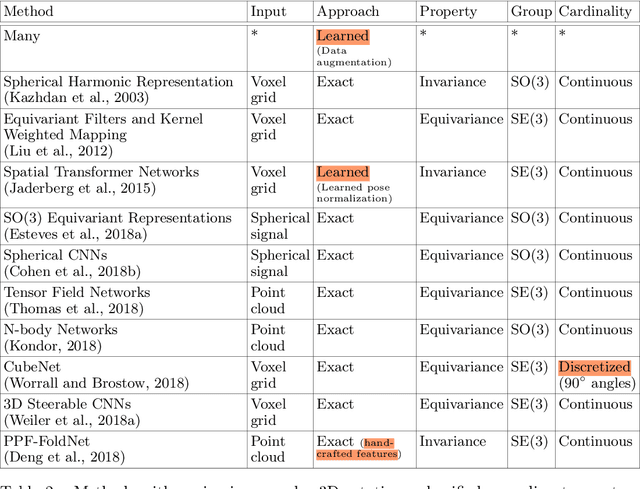
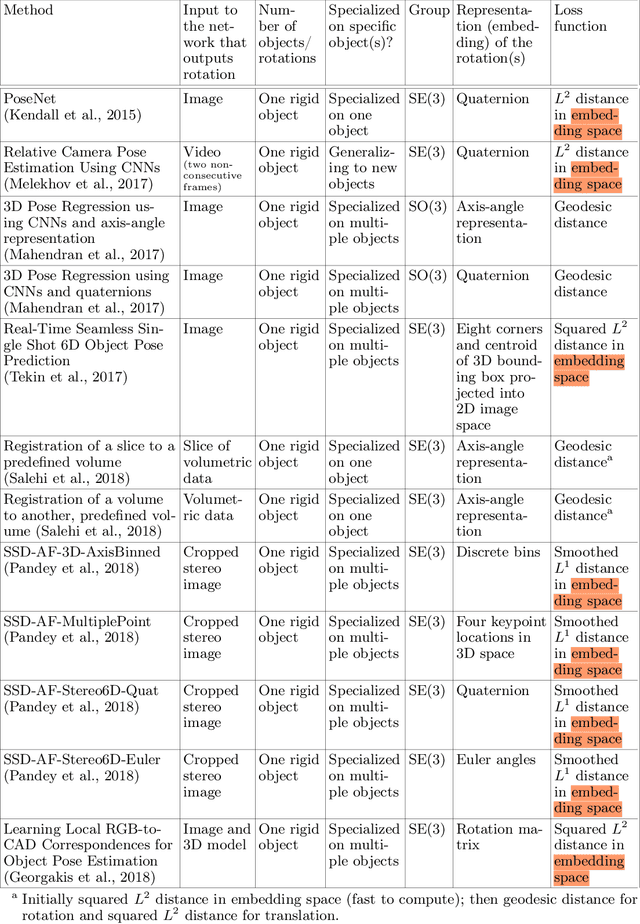
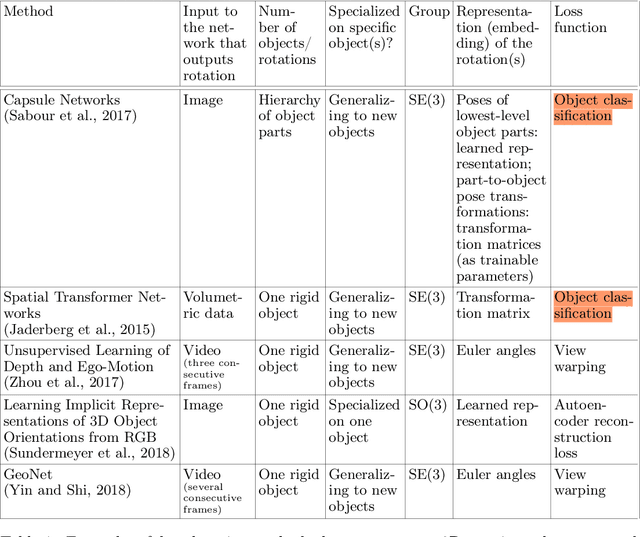
One of the reasons for the success of convolutional networks is their equivariance/invariance under translations. However, rotatable data such as molecules, living cells, everyday objects, or galaxies require processing with equivariance/invariance under rotations in cases where the rotation of the coordinate system does not affect the meaning of the data (e.g. object classification). On the other hand, estimation/processing of rotations is necessary in cases where rotations are important (e.g. motion estimation). There has been recent progress in methods and theory in all these regards. Here we provide an overview of existing methods, both for 2D and 3D rotations (and translations), and identify commonalities and links between them, in the hope that our insights will be useful for choosing and perfecting the methods.