Approximation and learning with compositional tensor trains

We introduce compositional tensor trains (CTTs) for the approximation of multivariate functions, a class of models obtained by composing low-rank functions in the tensor-train format. This format can encode standard approximation tools, such as (sparse) polynomials, deep neural networks (DNNs) with fixed width, or tensor networks with arbitrary permutation of the inputs, or more general affine coordinate transformations, with similar complexities. This format can be viewed as a DNN with width exponential in the input dimension and structured weights matrices. Compared to DNNs, this format enables controlled compression at the layer level using efficient tensor algebra. On the optimization side, we derive a layerwise algorithm inspired by natural gradient descent, allowing to exploit efficient low-rank tensor algebra. This relies on low-rank estimations of Gram matrices, and tensor structured random sketching. Viewing the format as a discrete dynamical system, we also derive an optimization algorithm inspired by numerical methods in optimal control. Numerical experiments on regression tasks demonstrate the expressivity of the new format and the relevance of the proposed optimization algorithms. Overall, CTTs combine the expressivity of compositional models with the algorithmic efficiency of tensor algebra, offering a scalable alternative to standard deep neural networks.

Surrogate to Poincaré inequalities on manifolds for dimension reduction in nonlinear feature spaces

We aim to approximate a continuously differentiable function $u:\mathbb{R}^d \rightarrow \mathbb{R}$ by a composition of functions $f\circ g$ where $g:\mathbb{R}^d \rightarrow \mathbb{R}^m$, $m\leq d$, and $f : \mathbb{R}^m \rightarrow \mathbb{R}$ are built in a two stage procedure. For a fixed $g$, we build $f$ using classical regression methods, involving evaluations of $u$. Recent works proposed to build a nonlinear $g$ by minimizing a loss function $\mathcal{J}(g)$ derived from Poincar\'e inequalities on manifolds, involving evaluations of the gradient of $u$. A problem is that minimizing $\mathcal{J}$ may be a challenging task. Hence in this work, we introduce new convex surrogates to $\mathcal{J}$. Leveraging concentration inequalities, we provide sub-optimality results for a class of functions $g$, including polynomials, and a wide class of input probability measures. We investigate performances on different benchmarks for various training sample sizes. We show that our approach outperforms standard iterative methods for minimizing the training Poincar\'e inequality based loss, often resulting in better approximation errors, especially for rather small training sets and $m=1$.

Weighted least-squares approximation with determinantal point processes and generalized volume sampling

We consider the problem of approximating a function from $L^2$ by an element of a given $m$-dimensional space $V_m$, associated with some feature map $\varphi$, using evaluations of the function at random points $x_1,\dots,x_n$. After recalling some results on optimal weighted least-squares using independent and identically distributed points, we consider weighted least-squares using projection determinantal point processes (DPP) or volume sampling. These distributions introduce dependence between the points that promotes diversity in the selected features $\varphi(x_i)$. We first provide a generalized version of volume-rescaled sampling yielding quasi-optimality results in expectation with a number of samples $n = O(m\log(m))$, that means that the expected $L^2$ error is bounded by a constant times the best approximation error in $L^2$. Also, further assuming that the function is in some normed vector space $H$ continuously embedded in $L^2$, we further prove that the approximation is almost surely bounded by the best approximation error measured in the $H$-norm. This includes the cases of functions from $L^\infty$ or reproducing kernel Hilbert spaces. Finally, we present an alternative strategy consisting in using independent repetitions of projection DPP (or volume sampling), yielding similar error bounds as with i.i.d. or volume sampling, but in practice with a much lower number of samples. Numerical experiments illustrate the performance of the different strategies.

Approximation with Tensor Networks. Part III: Multivariate Approximation

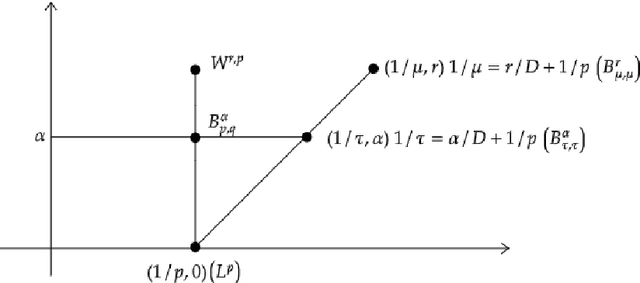
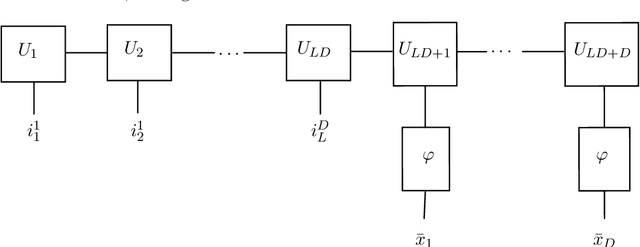
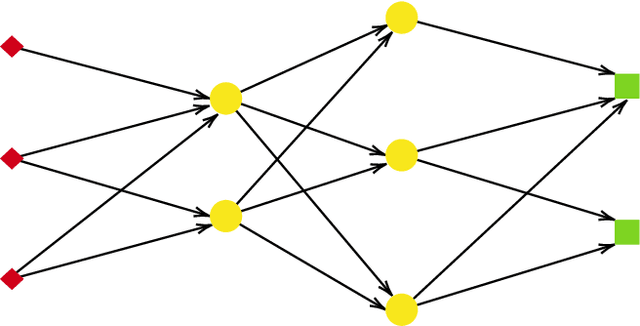
We study the approximation of multivariate functions with tensor networks (TNs). The main conclusion of this work is an answer to the following two questions: "What are the approximation capabilities of TNs?" and "What is an appropriate model class of functions that can be approximated with TNs?" To answer the former: we show that TNs can (near to) optimally replicate $h$-uniform and $h$-adaptive approximation, for any smoothness order of the target function. Tensor networks thus exhibit universal expressivity w.r.t. isotropic, anisotropic and mixed smoothness spaces that is comparable with more general neural networks families such as deep rectified linear unit (ReLU) networks. Put differently, TNs have the capacity to (near to) optimally approximate many function classes -- without being adapted to the particular class in question. To answer the latter: as a candidate model class we consider approximation classes of TNs and show that these are (quasi-)Banach spaces, that many types of classical smoothness spaces are continuously embedded into said approximation classes and that TN approximation classes are themselves not embedded in any classical smoothness space.

Approximation of Smoothness Classes by Deep ReLU Networks

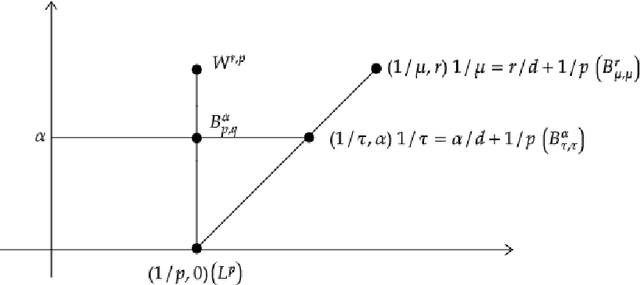
We consider approximation rates of sparsely connected deep rectified linear unit (ReLU) and rectified power unit (RePU) neural networks for functions in Besov spaces $B^\alpha_{q}(L^p)$ in arbitrary dimension $d$, on bounded or unbounded domains. We show that RePU networks with a fixed activation function attain optimal approximation rates for functions in the Besov space $B^\alpha_{\tau}(L^\tau)$ on the critical embedding line $1/\tau=\alpha/d+1/p$ for arbitrary smoothness order $\alpha>0$. Moreover, we show that ReLU networks attain near to optimal rates for any Besov space strictly above the critical line. Using interpolation theory, this implies that the entire range of smoothness classes at or above the critical line is (near to) optimally approximated by deep ReLU/RePU networks.

A PAC algorithm in relative precision for bandit problem with costly sampling

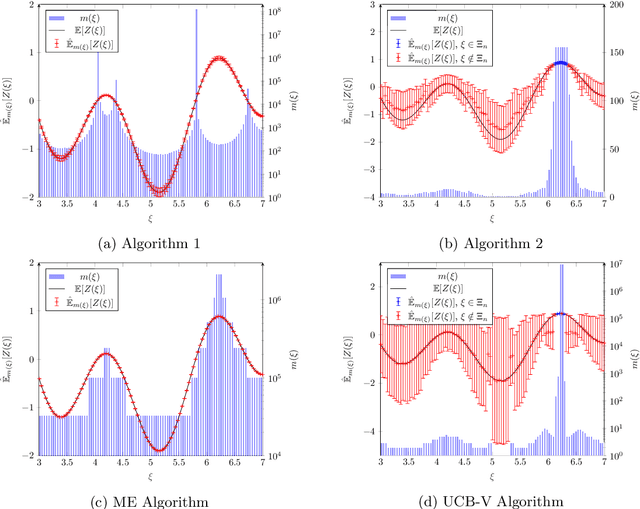
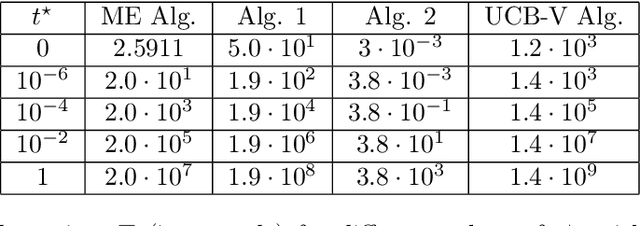
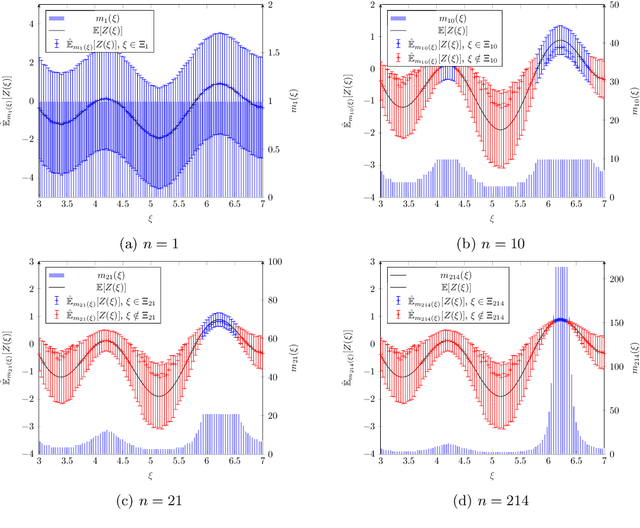
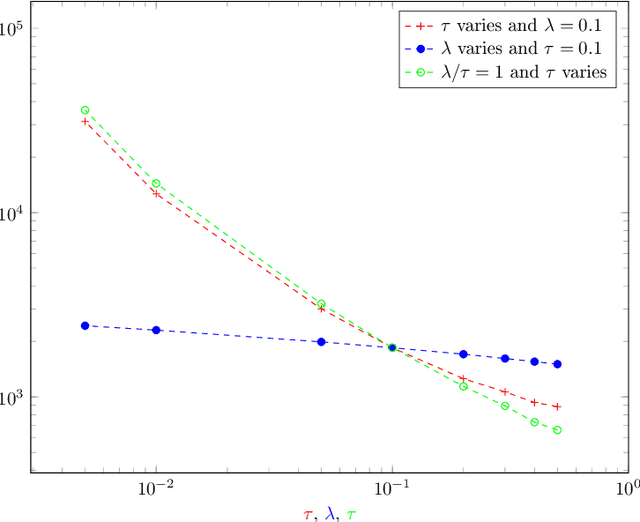
This paper considers the problem of maximizing an expectation function over a finite set, or finite-arm bandit problem. We first propose a naive stochastic bandit algorithm for obtaining a probably approximately correct (PAC) solution to this discrete optimization problem in relative precision, that is a solution which solves the optimization problem up to a relative error smaller than a prescribed tolerance, with high probability. We also propose an adaptive stochastic bandit algorithm which provides a PAC-solution with the same guarantees. The adaptive algorithm outperforms the mean complexity of the naive algorithm in terms of number of generated samples and is particularly well suited for applications with high sampling cost.

Learning with tree tensor networks: complexity estimates and model selection

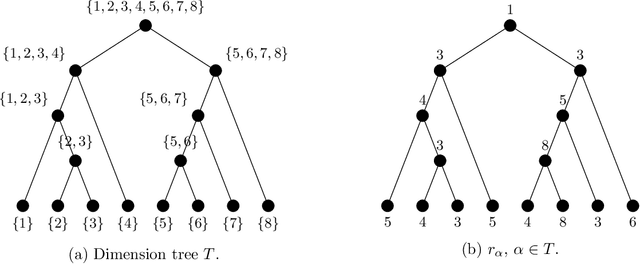
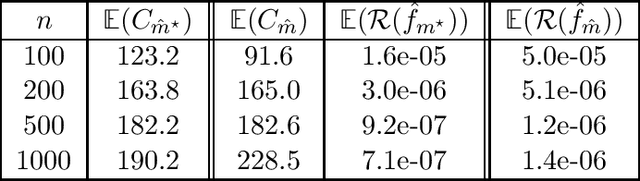
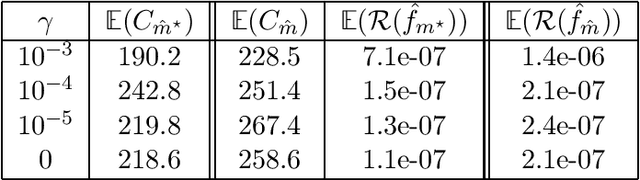
In this paper, we propose and analyze a model selection method for tree tensor networks in an empirical risk minimization framework. Tree tensor networks, or tree-based tensor formats, are prominent model classes for the approximation of high-dimensional functions in numerical analysis and data science. They correspond to sum-product neural networks with a sparse connectivity associated with a dimension partition tree $T$, widths given by a tuple $r$ of tensor ranks, and multilinear activation functions (or units). The approximation power of these model classes has been proved to be near-optimal for classical smoothness classes. However, in an empirical risk minimization framework with a limited number of observations, the dimension tree $T$ and ranks $r$ should be selected carefully to balance estimation and approximation errors. In this paper, we propose a complexity-based model selection strategy \`a la Barron, Birg\'e, Massart. Given a family of model classes, with different trees, ranks and tensor product feature spaces, a model is selected by minimizing a penalized empirical risk, with a penalty depending on the complexity of the model class. After deriving bounds of the metric entropy of tree tensor networks with bounded parameters, we deduce a form of the penalty from bounds on suprema of empirical processes. This choice of penalty yields a risk bound for the predictor associated with the selected model. For classical smoothness spaces, we show that the proposed strategy is minimax optimal in a least-squares setting. In practice, the amplitude of the penalty is calibrated with a slope heuristics method. Numerical experiments in a least-squares regression setting illustrate the performance of the strategy for the approximation of multivariate functions and univariate functions identified with tensors by tensorization (quantization).

Approximation with Tensor Networks. Part II: Approximation Rates for Smoothness Classes

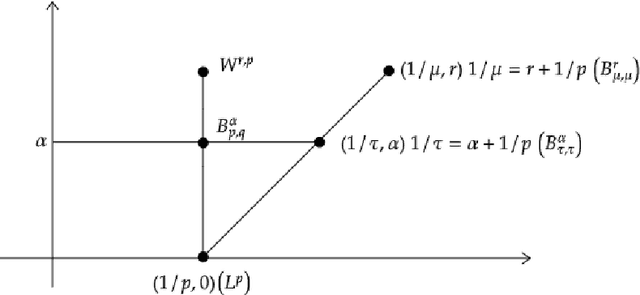
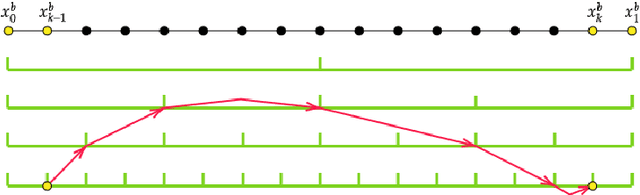
We study the approximation by tensor networks (TNs) of functions from classical smoothness classes. The considered approximation tool combines a tensorization of functions in $L^p([0,1))$, which allows to identify a univariate function with a multivariate function (or tensor), and the use of tree tensor networks (the tensor train format) for exploiting low-rank structures of multivariate functions. The resulting tool can be interpreted as a feed-forward neural network, with first layers implementing the tensorization, interpreted as a particular featuring step, followed by a sum-product network with sparse architecture. In part I of this work, we presented several approximation classes associated with different measures of complexity of tensor networks and studied their properties. In this work (part II), we show how classical approximation tools, such as polynomials or splines (with fixed or free knots), can be encoded as a tensor network with controlled complexity. We use this to derive direct (Jackson) inequalities for the approximation spaces of tensor networks. This is then utilized to show that Besov spaces are continuously embedded into these approximation spaces. In other words, we show that arbitrary Besov functions can be approximated with optimal or near to optimal rate. We also show that an arbitrary function in the approximation class possesses no Besov smoothness, unless one limits the depth of the tensor network.

Approximation with Tensor Networks. Part I: Approximation Spaces

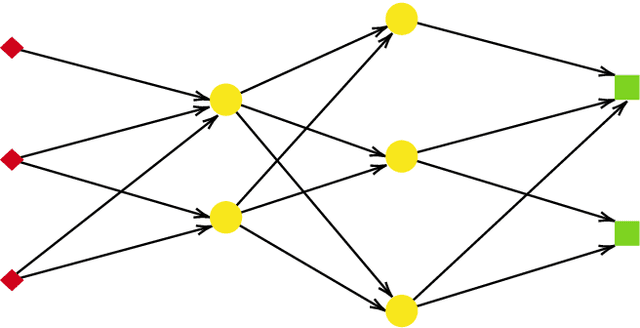
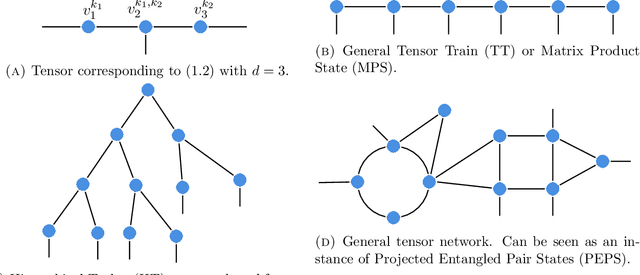
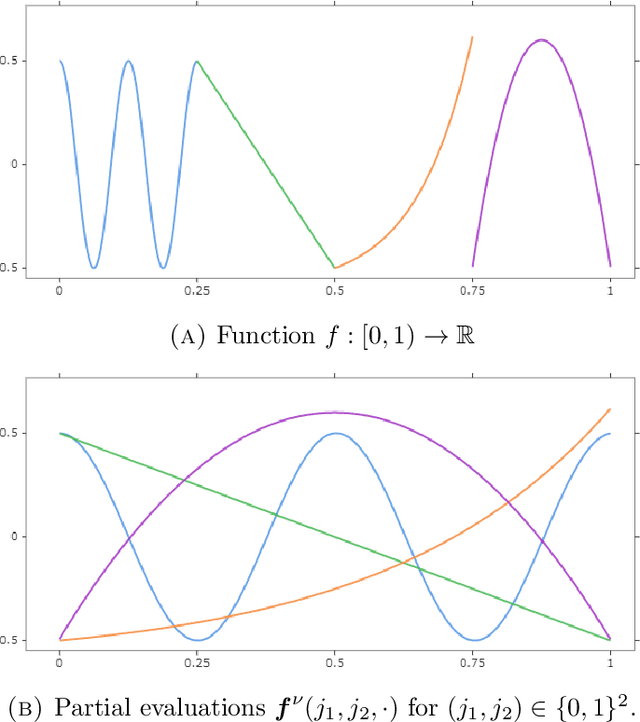
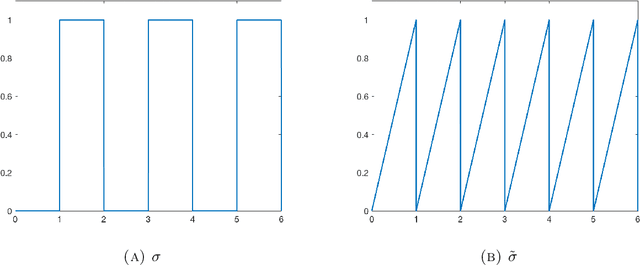
We study the approximation of functions by tensor networks (TNs). We show that Lebesgue $L^p$-spaces in one dimension can be identified with tensor product spaces of arbitrary order through tensorization. We use this tensor product structure to define subsets of $L^p$ of rank-structured functions of finite representation complexity. These subsets are then used to define different approximation classes of tensor networks, associated with different measures of complexity. These approximation classes are shown to be quasi-normed linear spaces. We study some elementary properties and relationships of said spaces. In part II of this work, we will show that classical smoothness (Besov) spaces are continuously embedded into these approximation classes. We will also show that functions in these approximation classes do not possess any Besov smoothness, unless one restricts the depth of the tensor networks. The results of this work are both an analysis of the approximation spaces of TNs and a study of the expressivity of a particular type of neural networks (NN) -- namely feed-forward sum-product networks with sparse architecture. The input variables of this network result from the tensorization step, interpreted as a particular featuring step which can also be implemented with a neural network with a specific architecture. We point out interesting parallels to recent results on the expressivity of rectified linear unit (ReLU) networks -- currently one of the most popular type of NNs.

Learning high-dimensional probability distributions using tree tensor networks

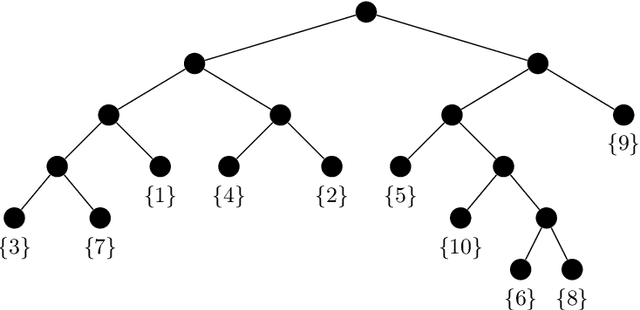
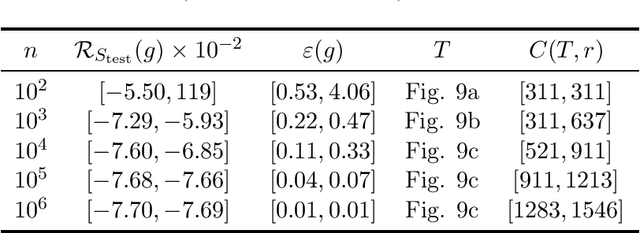
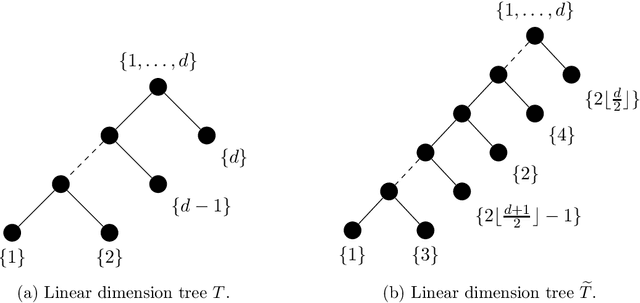
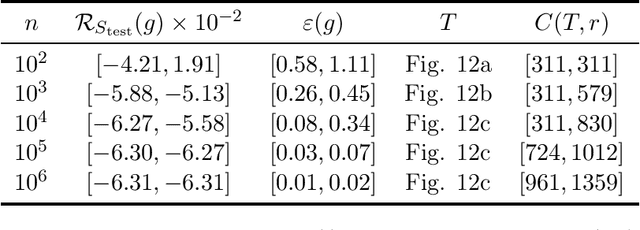
We consider the problem of the estimation of a high-dimensional probability distribution using model classes of functions in tree-based tensor formats, a particular case of tensor networks associated with a dimension partition tree. The distribution is assumed to admit a density with respect to a product measure, possibly discrete for handling the case of discrete random variables. After discussing the representation of classical model classes in tree-based tensor formats, we present learning algorithms based on empirical risk minimization using a $L^2$ contrast. These algorithms exploit the multilinear parametrization of the formats to recast the nonlinear minimization problem into a sequence of empirical risk minimization problems with linear models. A suitable parametrization of the tensor in tree-based tensor format allows to obtain a linear model with orthogonal bases, so that each problem admits an explicit expression of the solution and cross-validation risk estimates. These estimations of the risk enable the model selection, for instance when exploiting sparsity in the coefficients of the representation. A strategy for the adaptation of the tensor format (dimension tree and tree-based ranks) is provided, which allows to discover and exploit some specific structures of high-dimensional probability distributions such as independence or conditional independence. We illustrate the performances of the proposed algorithms for the approximation of classical probabilistic models (such as Gaussian distribution, graphical models, Markov chain).