Approximation with Tensor Networks. Part III: Multivariate Approximation

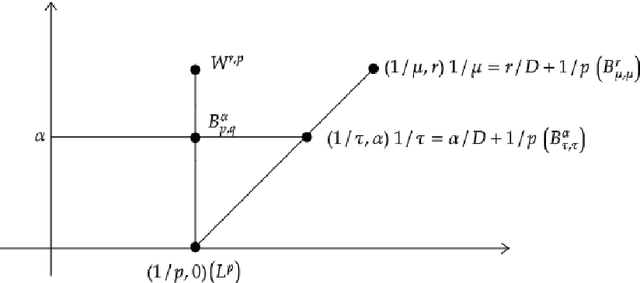
We study the approximation of multivariate functions with tensor networks (TNs). The main conclusion of this work is an answer to the following two questions: "What are the approximation capabilities of TNs?" and "What is an appropriate model class of functions that can be approximated with TNs?" To answer the former: we show that TNs can (near to) optimally replicate $h$-uniform and $h$-adaptive approximation, for any smoothness order of the target function. Tensor networks thus exhibit universal expressivity w.r.t. isotropic, anisotropic and mixed smoothness spaces that is comparable with more general neural networks families such as deep rectified linear unit (ReLU) networks. Put differently, TNs have the capacity to (near to) optimally approximate many function classes -- without being adapted to the particular class in question. To answer the latter: as a candidate model class we consider approximation classes of TNs and show that these are (quasi-)Banach spaces, that many types of classical smoothness spaces are continuously embedded into said approximation classes and that TN approximation classes are themselves not embedded in any classical smoothness space.

Approximation of Smoothness Classes by Deep ReLU Networks

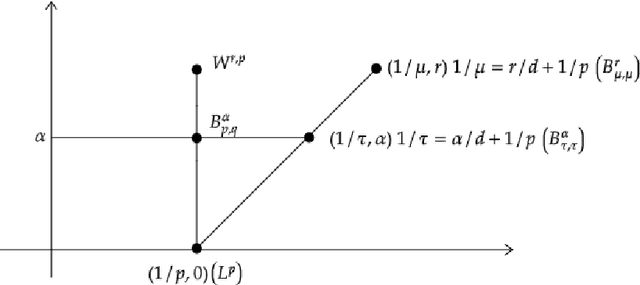
We consider approximation rates of sparsely connected deep rectified linear unit (ReLU) and rectified power unit (RePU) neural networks for functions in Besov spaces $B^\alpha_{q}(L^p)$ in arbitrary dimension $d$, on bounded or unbounded domains. We show that RePU networks with a fixed activation function attain optimal approximation rates for functions in the Besov space $B^\alpha_{\tau}(L^\tau)$ on the critical embedding line $1/\tau=\alpha/d+1/p$ for arbitrary smoothness order $\alpha>0$. Moreover, we show that ReLU networks attain near to optimal rates for any Besov space strictly above the critical line. Using interpolation theory, this implies that the entire range of smoothness classes at or above the critical line is (near to) optimally approximated by deep ReLU/RePU networks.

Approximation with Tensor Networks. Part II: Approximation Rates for Smoothness Classes

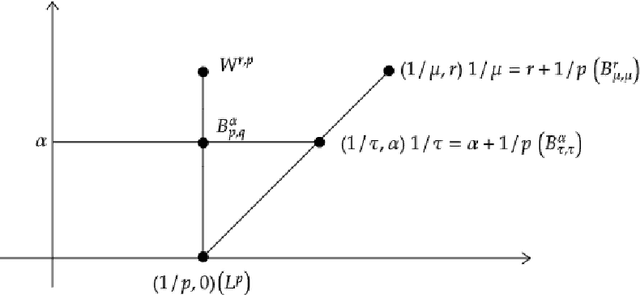
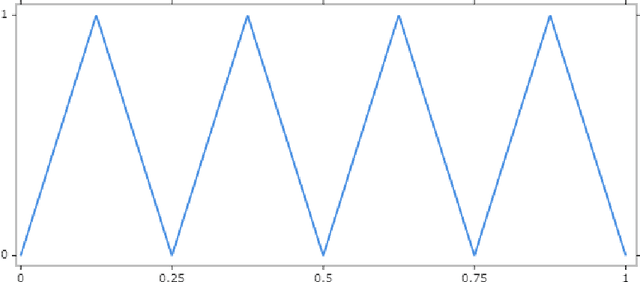
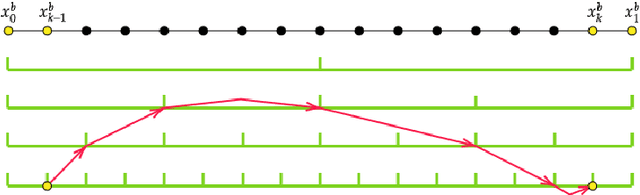
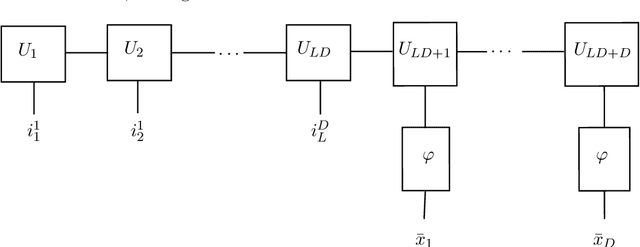
We study the approximation by tensor networks (TNs) of functions from classical smoothness classes. The considered approximation tool combines a tensorization of functions in $L^p([0,1))$, which allows to identify a univariate function with a multivariate function (or tensor), and the use of tree tensor networks (the tensor train format) for exploiting low-rank structures of multivariate functions. The resulting tool can be interpreted as a feed-forward neural network, with first layers implementing the tensorization, interpreted as a particular featuring step, followed by a sum-product network with sparse architecture. In part I of this work, we presented several approximation classes associated with different measures of complexity of tensor networks and studied their properties. In this work (part II), we show how classical approximation tools, such as polynomials or splines (with fixed or free knots), can be encoded as a tensor network with controlled complexity. We use this to derive direct (Jackson) inequalities for the approximation spaces of tensor networks. This is then utilized to show that Besov spaces are continuously embedded into these approximation spaces. In other words, we show that arbitrary Besov functions can be approximated with optimal or near to optimal rate. We also show that an arbitrary function in the approximation class possesses no Besov smoothness, unless one limits the depth of the tensor network.

Approximation with Tensor Networks. Part I: Approximation Spaces

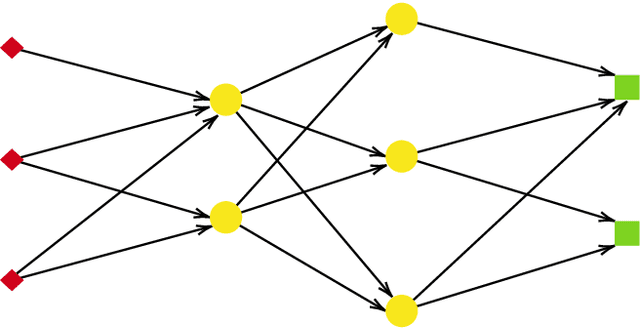
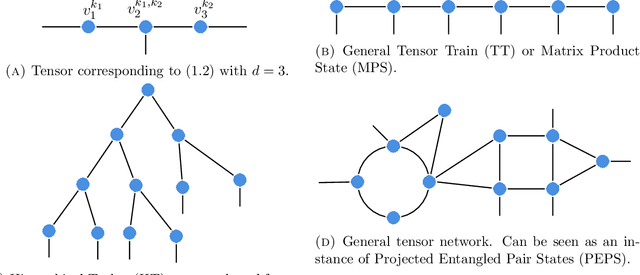
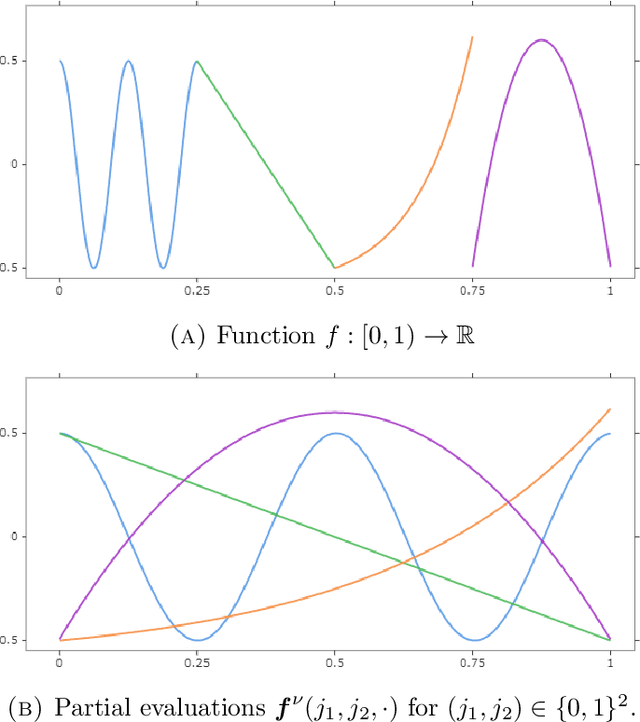
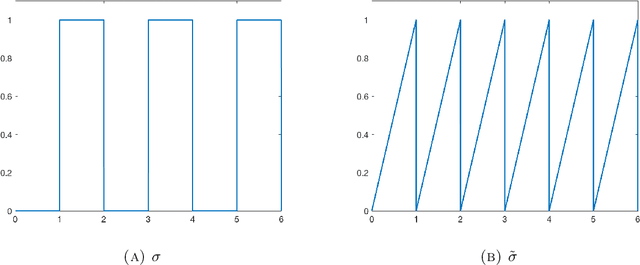
We study the approximation of functions by tensor networks (TNs). We show that Lebesgue $L^p$-spaces in one dimension can be identified with tensor product spaces of arbitrary order through tensorization. We use this tensor product structure to define subsets of $L^p$ of rank-structured functions of finite representation complexity. These subsets are then used to define different approximation classes of tensor networks, associated with different measures of complexity. These approximation classes are shown to be quasi-normed linear spaces. We study some elementary properties and relationships of said spaces. In part II of this work, we will show that classical smoothness (Besov) spaces are continuously embedded into these approximation classes. We will also show that functions in these approximation classes do not possess any Besov smoothness, unless one restricts the depth of the tensor networks. The results of this work are both an analysis of the approximation spaces of TNs and a study of the expressivity of a particular type of neural networks (NN) -- namely feed-forward sum-product networks with sparse architecture. The input variables of this network result from the tensorization step, interpreted as a particular featuring step which can also be implemented with a neural network with a specific architecture. We point out interesting parallels to recent results on the expressivity of rectified linear unit (ReLU) networks -- currently one of the most popular type of NNs.