Approximation with Tensor Networks. Part III: Multivariate Approximation

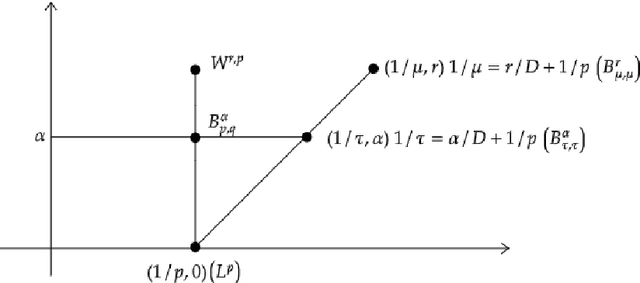
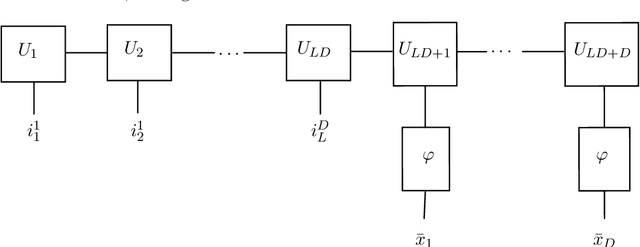
We study the approximation of multivariate functions with tensor networks (TNs). The main conclusion of this work is an answer to the following two questions: "What are the approximation capabilities of TNs?" and "What is an appropriate model class of functions that can be approximated with TNs?" To answer the former: we show that TNs can (near to) optimally replicate $h$-uniform and $h$-adaptive approximation, for any smoothness order of the target function. Tensor networks thus exhibit universal expressivity w.r.t. isotropic, anisotropic and mixed smoothness spaces that is comparable with more general neural networks families such as deep rectified linear unit (ReLU) networks. Put differently, TNs have the capacity to (near to) optimally approximate many function classes -- without being adapted to the particular class in question. To answer the latter: as a candidate model class we consider approximation classes of TNs and show that these are (quasi-)Banach spaces, that many types of classical smoothness spaces are continuously embedded into said approximation classes and that TN approximation classes are themselves not embedded in any classical smoothness space.