Learning with tree-based tensor formats

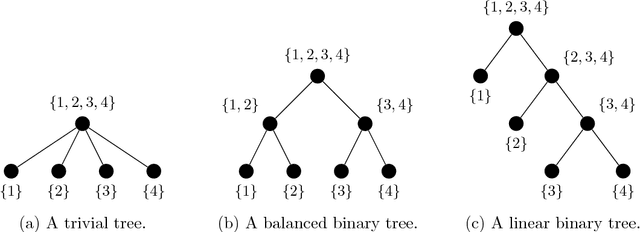
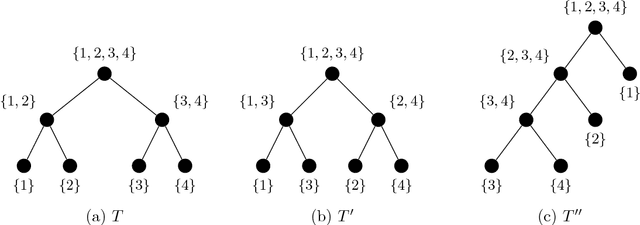
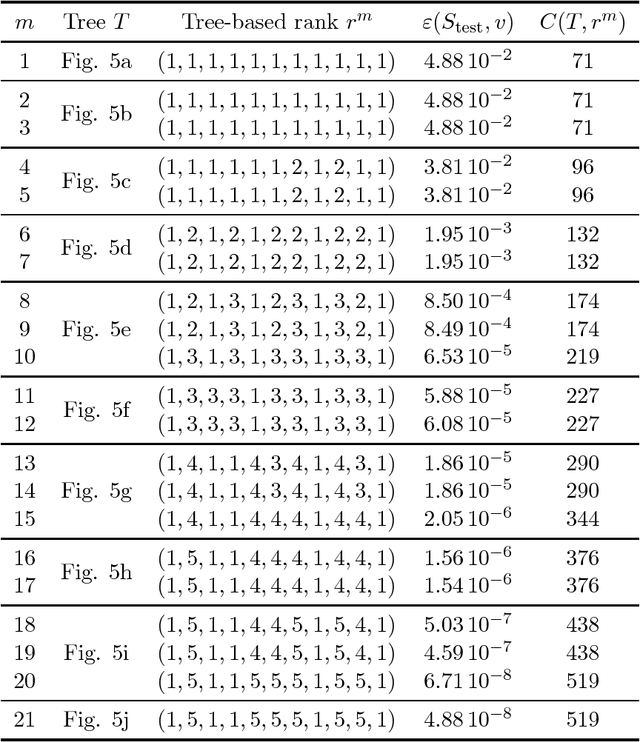
This paper is concerned with the approximation of high-dimensional functions in a statistical learning setting, by empirical risk minimization over model classes of functions in tree-based tensor format. These are particular classes of rank-structured functions that can be seen as deep neural networks with a sparse architecture related to the tree and multilinear activation functions. For learning in a given model class, we exploit the fact that tree-based tensor formats are multilinear models and recast the problem of risk minimization over a nonlinear set into a succession of learning problems with linear models. Suitable changes of representation yield numerically stable learning problems and allow to exploit sparsity. For high-dimensional problems or when only a small data set is available, the selection of a good model class is a critical issue. For a given tree, the selection of the tuple of tree-based ranks that minimize the risk is a combinatorial problem. Here, we propose a rank adaptation strategy which provides in practice a good convergence of the risk as a function of the model class complexity. Finding a good tree is also a combinatorial problem, which can be related to the choice of a particular sparse architecture for deep neural networks. Here, we propose a stochastic algorithm for minimizing the complexity of the representation of a given function over a class of trees with a given arity, allowing changes in the topology of the tree. This tree optimization algorithm is then included in a learning scheme that successively adapts the tree and the corresponding tree-based ranks. Contrary to classical learning algorithms for nonlinear model classes, the proposed algorithms are numerically stable, reliable, and require only a low level expertise of the user.

A least-squares method for sparse low rank approximation of multivariate functions

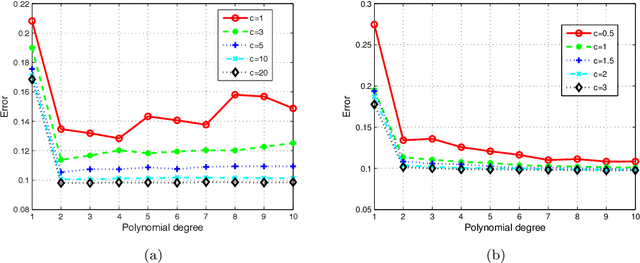
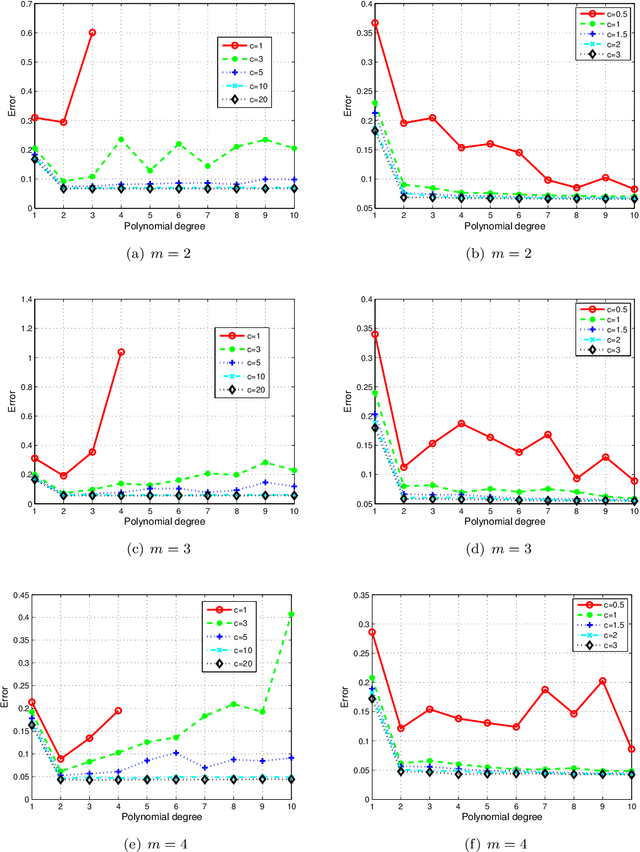
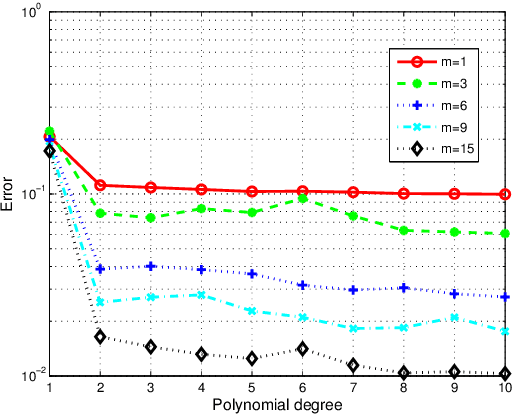
In this paper, we propose a low-rank approximation method based on discrete least-squares for the approximation of a multivariate function from random, noisy-free observations. Sparsity inducing regularization techniques are used within classical algorithms for low-rank approximation in order to exploit the possible sparsity of low-rank approximations. Sparse low-rank approximations are constructed with a robust updated greedy algorithm which includes an optimal selection of regularization parameters and approximation ranks using cross validation techniques. Numerical examples demonstrate the capability of approximating functions of many variables even when very few function evaluations are available, thus proving the interest of the proposed algorithm for the propagation of uncertainties through complex computational models.