Detection of Thermal Events by Semi-Supervised Learning for Tokamak First Wall Safety

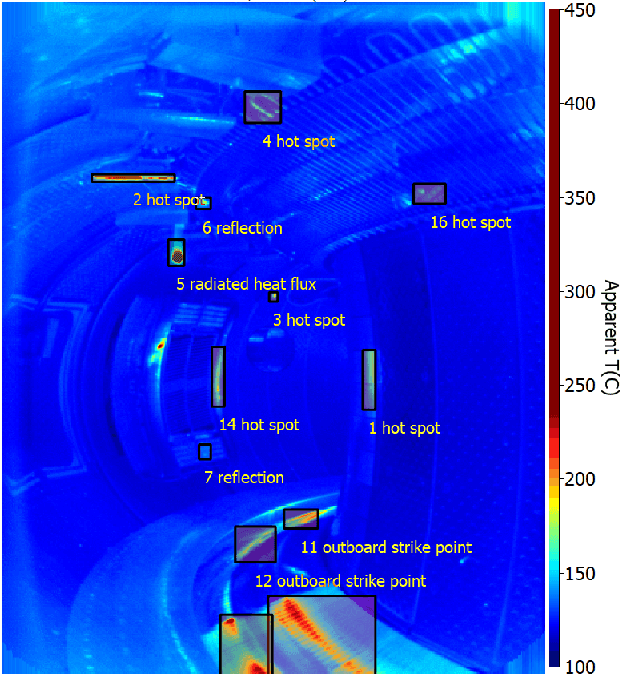
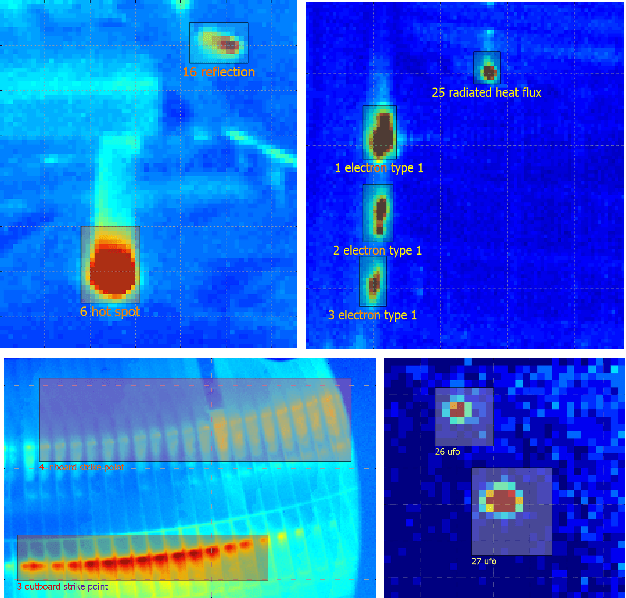
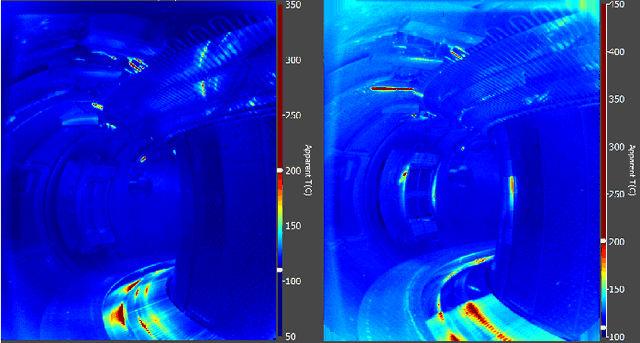
This paper explores a semi-supervised object detection approach to detect hot spots on the internal wall of Tokamaks. A huge amount of data is produced during an experimental campaign by the infrared (IR) viewing systems used to monitor the inner thermal shields during machine operation. The amount of data to be processed and analysed is such that protecting the first wall is an overwhelming job. Automatizing this job with artificial intelligence (AI) is an attractive solution, but AI requires large labelled databases which are not readily available for Tokamak walls. Semi-supervised learning (SSL) is a possible solution to being able to train deep learning models with a small amount of labelled data and a large amount of unlabelled data. SSL is explored as a possible tool to rapidly adapt a model trained on an experimental campaign A of Tokamak WEST to a new experimental campaign B by using labelled data from campaign A, a little labelled data from campaign B and a lot of unlabelled data from campaign B. Model performances are evaluated on two labelled datasets and two methods including semi-supervised learning. Semi-supervised learning increased the mAP metric by over six percentage points on the first smaller scale database and over four percentage points on the second larger scale dataset depending on the employed method.

Learning high-dimensional probability distributions using tree tensor networks

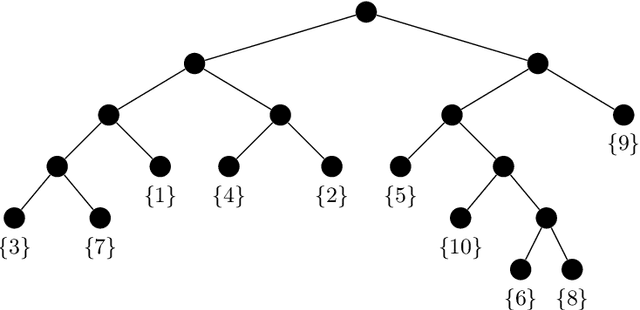
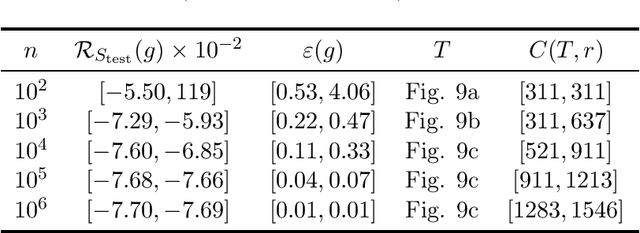
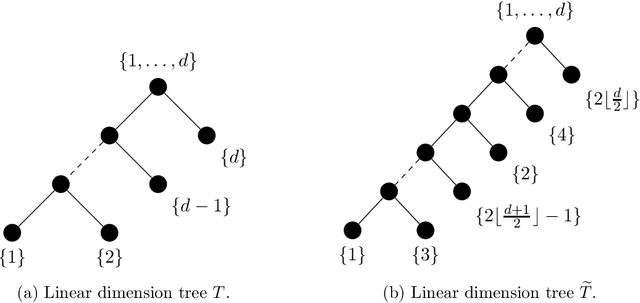
We consider the problem of the estimation of a high-dimensional probability distribution using model classes of functions in tree-based tensor formats, a particular case of tensor networks associated with a dimension partition tree. The distribution is assumed to admit a density with respect to a product measure, possibly discrete for handling the case of discrete random variables. After discussing the representation of classical model classes in tree-based tensor formats, we present learning algorithms based on empirical risk minimization using a $L^2$ contrast. These algorithms exploit the multilinear parametrization of the formats to recast the nonlinear minimization problem into a sequence of empirical risk minimization problems with linear models. A suitable parametrization of the tensor in tree-based tensor format allows to obtain a linear model with orthogonal bases, so that each problem admits an explicit expression of the solution and cross-validation risk estimates. These estimations of the risk enable the model selection, for instance when exploiting sparsity in the coefficients of the representation. A strategy for the adaptation of the tensor format (dimension tree and tree-based ranks) is provided, which allows to discover and exploit some specific structures of high-dimensional probability distributions such as independence or conditional independence. We illustrate the performances of the proposed algorithms for the approximation of classical probabilistic models (such as Gaussian distribution, graphical models, Markov chain).

Learning with tree-based tensor formats

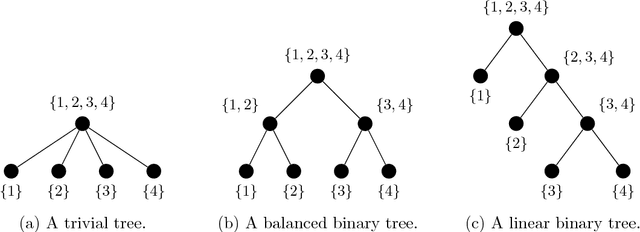
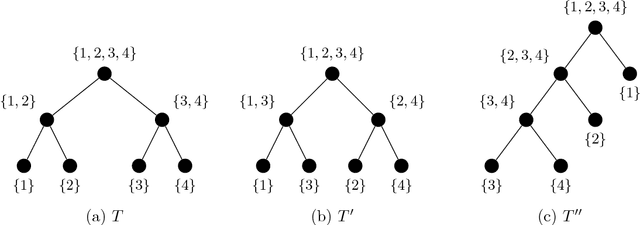
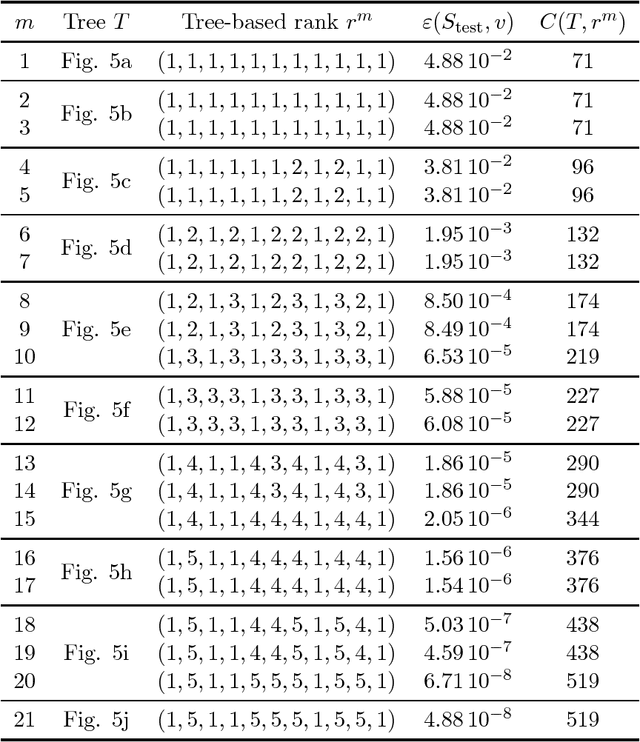
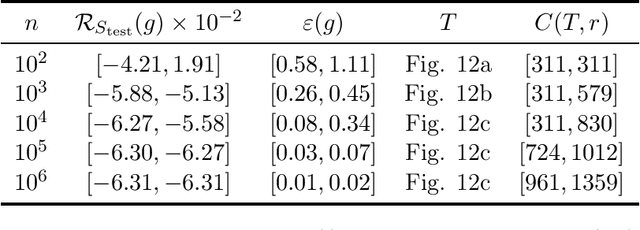
This paper is concerned with the approximation of high-dimensional functions in a statistical learning setting, by empirical risk minimization over model classes of functions in tree-based tensor format. These are particular classes of rank-structured functions that can be seen as deep neural networks with a sparse architecture related to the tree and multilinear activation functions. For learning in a given model class, we exploit the fact that tree-based tensor formats are multilinear models and recast the problem of risk minimization over a nonlinear set into a succession of learning problems with linear models. Suitable changes of representation yield numerically stable learning problems and allow to exploit sparsity. For high-dimensional problems or when only a small data set is available, the selection of a good model class is a critical issue. For a given tree, the selection of the tuple of tree-based ranks that minimize the risk is a combinatorial problem. Here, we propose a rank adaptation strategy which provides in practice a good convergence of the risk as a function of the model class complexity. Finding a good tree is also a combinatorial problem, which can be related to the choice of a particular sparse architecture for deep neural networks. Here, we propose a stochastic algorithm for minimizing the complexity of the representation of a given function over a class of trees with a given arity, allowing changes in the topology of the tree. This tree optimization algorithm is then included in a learning scheme that successively adapts the tree and the corresponding tree-based ranks. Contrary to classical learning algorithms for nonlinear model classes, the proposed algorithms are numerically stable, reliable, and require only a low level expertise of the user.