A least-squares method for sparse low rank approximation of multivariate functions

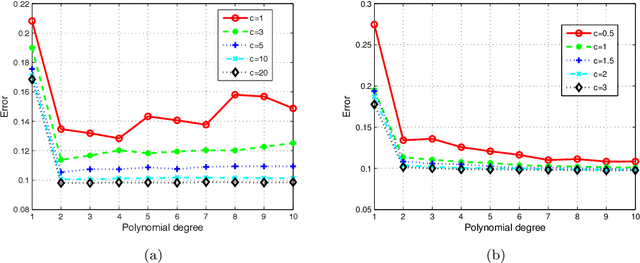
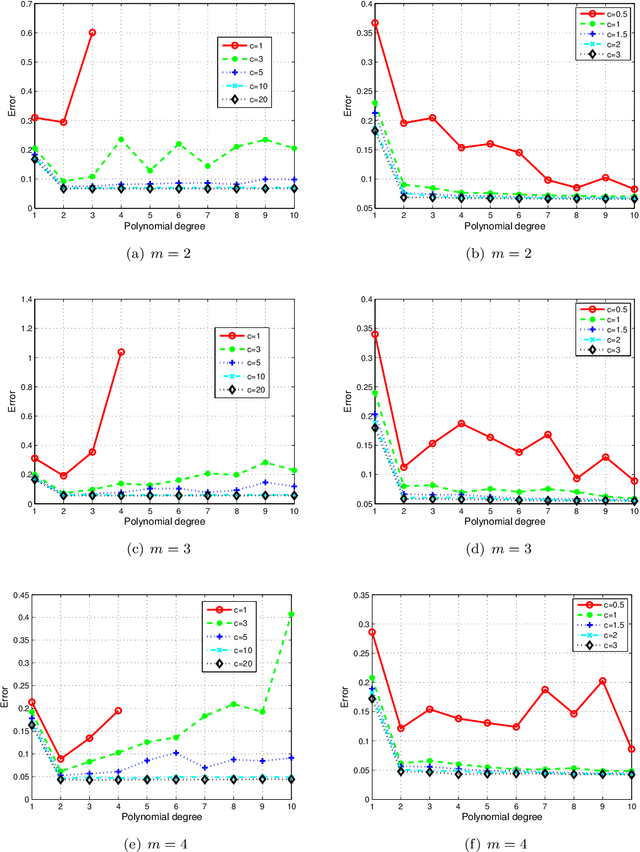
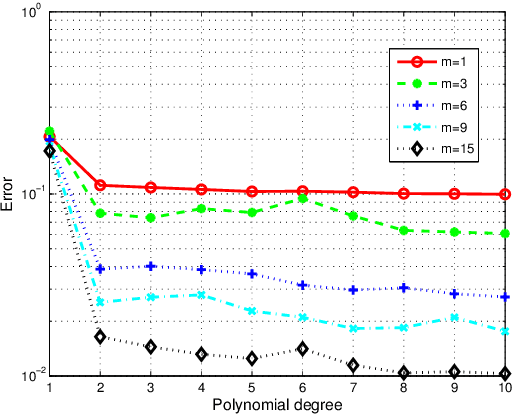
In this paper, we propose a low-rank approximation method based on discrete least-squares for the approximation of a multivariate function from random, noisy-free observations. Sparsity inducing regularization techniques are used within classical algorithms for low-rank approximation in order to exploit the possible sparsity of low-rank approximations. Sparse low-rank approximations are constructed with a robust updated greedy algorithm which includes an optimal selection of regularization parameters and approximation ranks using cross validation techniques. Numerical examples demonstrate the capability of approximating functions of many variables even when very few function evaluations are available, thus proving the interest of the proposed algorithm for the propagation of uncertainties through complex computational models.