In narrative texts punctuation marks obey the same statistics as words

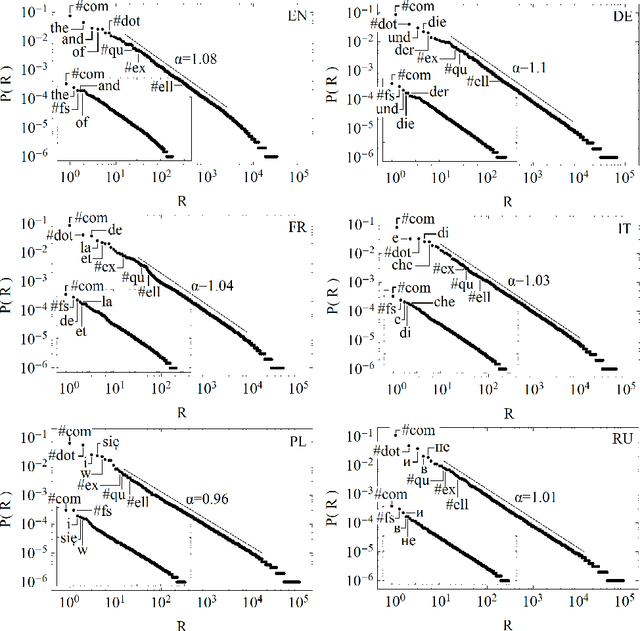
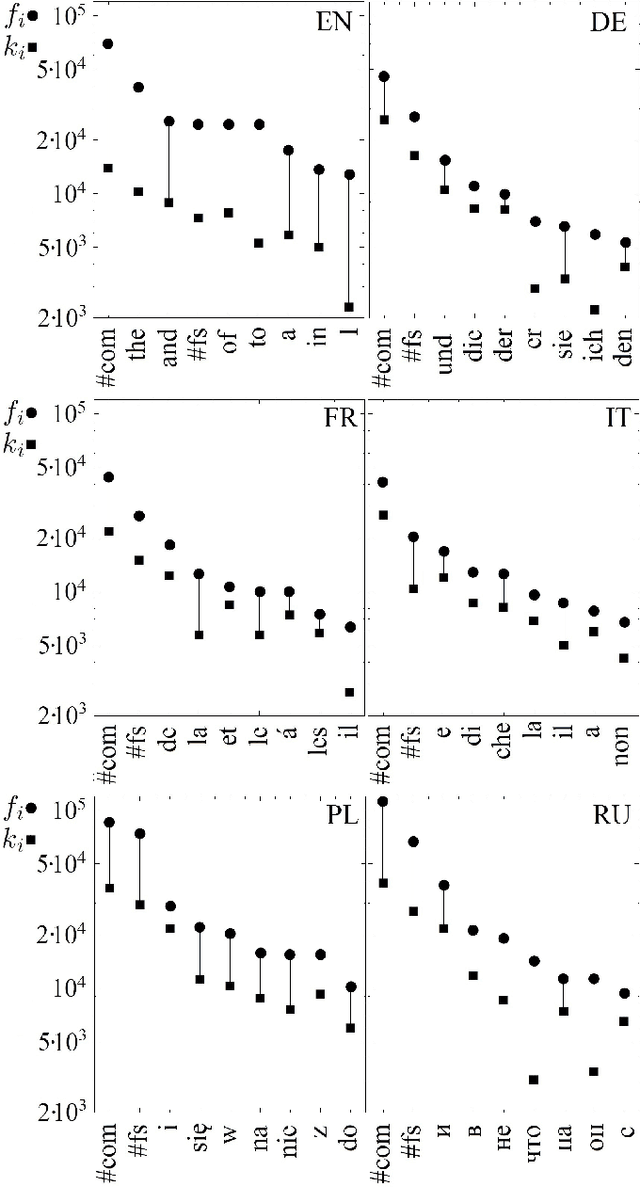
From a grammar point of view, the role of punctuation marks in a sentence is formally defined and well understood. In semantic analysis punctuation plays also a crucial role as a method of avoiding ambiguity of the meaning. A different situation can be observed in the statistical analyses of language samples, where the decision on whether the punctuation marks should be considered or should be neglected is seen rather as arbitrary and at present it belongs to a researcher's preference. An objective of this work is to shed some light onto this problem by providing us with an answer to the question whether the punctuation marks may be treated as ordinary words and whether they should be included in any analysis of the word co-occurences. We already know from our previous study (S.~Dro\.zd\.z {\it et al.}, Inf. Sci. 331 (2016) 32-44) that full stops that determine the length of sentences are the main carrier of long-range correlations. Now we extend that study and analyze statistical properties of the most common punctuation marks in a few Indo-European languages, investigate their frequencies, and locate them accordingly in the Zipf rank-frequency plots as well as study their role in the word-adjacency networks. We show that, from a statistical viewpoint, the punctuation marks reveal properties that are qualitatively similar to the properties of the most frequent words like articles, conjunctions, pronouns, and prepositions. This refers to both the Zipfian analysis and the network analysis. By adding the punctuation marks to the Zipf plots, we also show that these plots that are normally described by the Zipf-Mandelbrot distribution largely restore the power-law Zipfian behaviour for the most frequent items.

Quantifying origin and character of long-range correlations in narrative texts

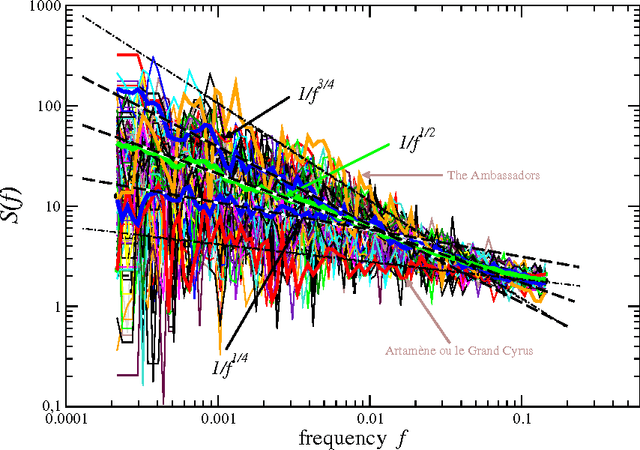
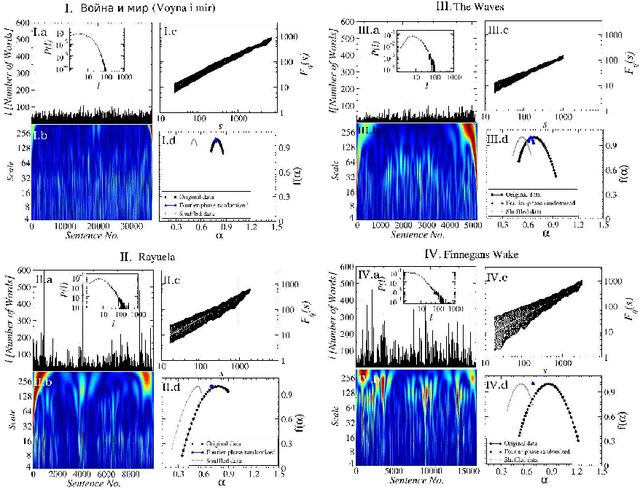
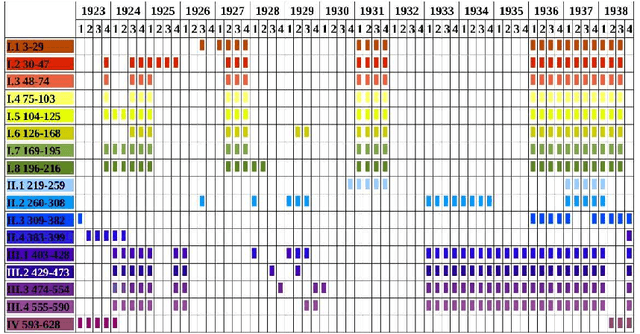
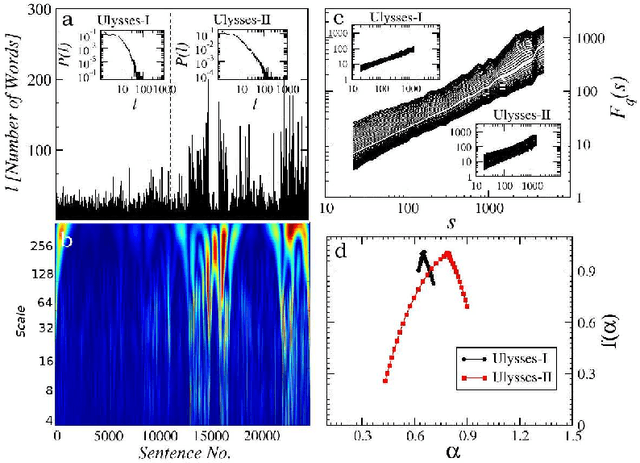
In natural language using short sentences is considered efficient for communication. However, a text composed exclusively of such sentences looks technical and reads boring. A text composed of long ones, on the other hand, demands significantly more effort for comprehension. Studying characteristics of the sentence length variability (SLV) in a large corpus of world-famous literary texts shows that an appealing and aesthetic optimum appears somewhere in between and involves selfsimilar, cascade-like alternation of various lengths sentences. A related quantitative observation is that the power spectra S(f) of thus characterized SLV universally develop a convincing `1/f^beta' scaling with the average exponent beta =~ 1/2, close to what has been identified before in musical compositions or in the brain waves. An overwhelming majority of the studied texts simply obeys such fractal attributes but especially spectacular in this respect are hypertext-like, "stream of consciousness" novels. In addition, they appear to develop structures characteristic of irreducibly interwoven sets of fractals called multifractals. Scaling of S(f) in the present context implies existence of the long-range correlations in texts and appearance of multifractality indicates that they carry even a nonlinear component. A distinct role of the full stops in inducing the long-range correlations in texts is evidenced by the fact that the above quantitative characteristics on the long-range correlations manifest themselves in variation of the full stops recurrence times along texts, thus in SLV, but to a much lesser degree in the recurrence times of the most frequent words. In this latter case the nonlinear correlations, thus multifractality, disappear even completely for all the texts considered. Treated as one extra word, the full stops at the same time appear to obey the Zipfian rank-frequency distribution, however.

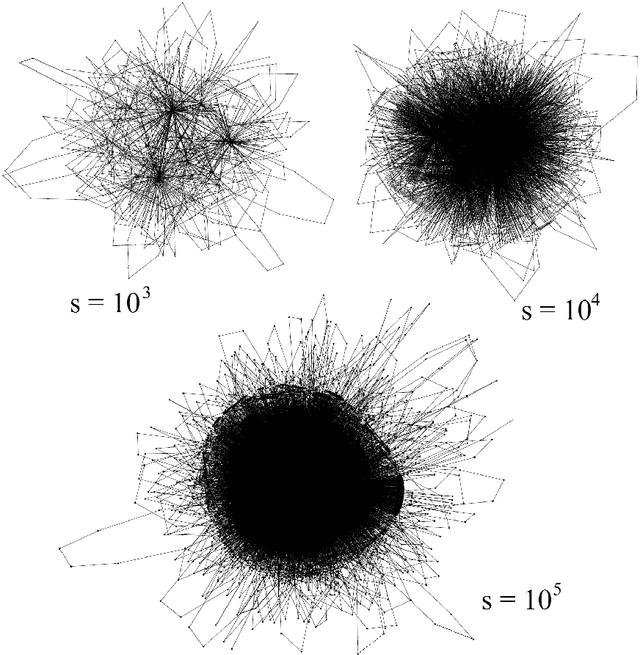
Modeling the average shortest path length in growth of word-adjacency networks

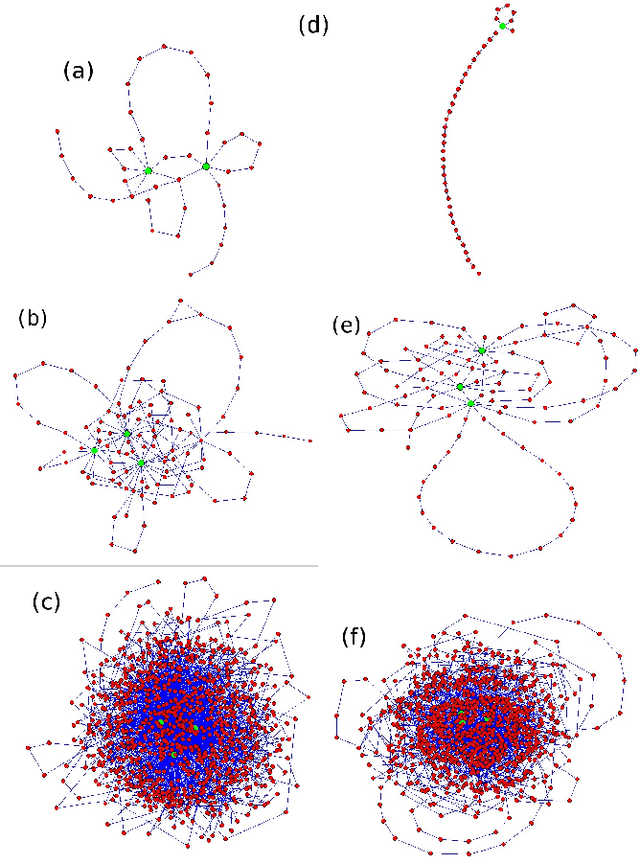
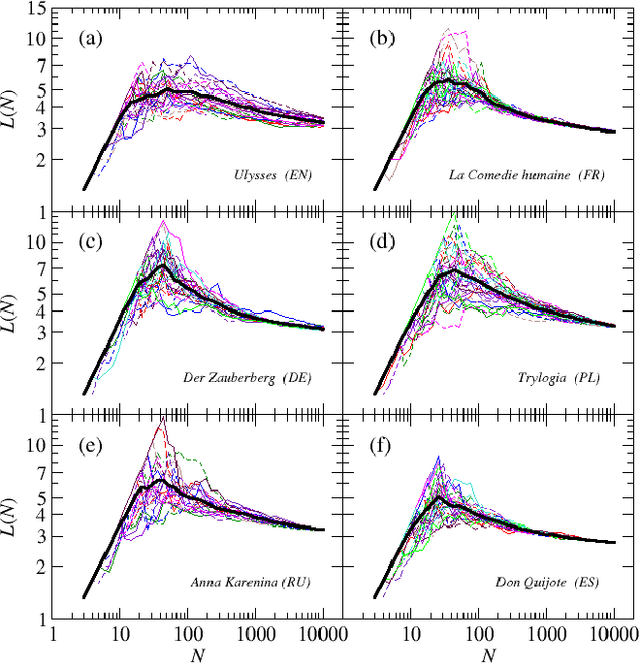
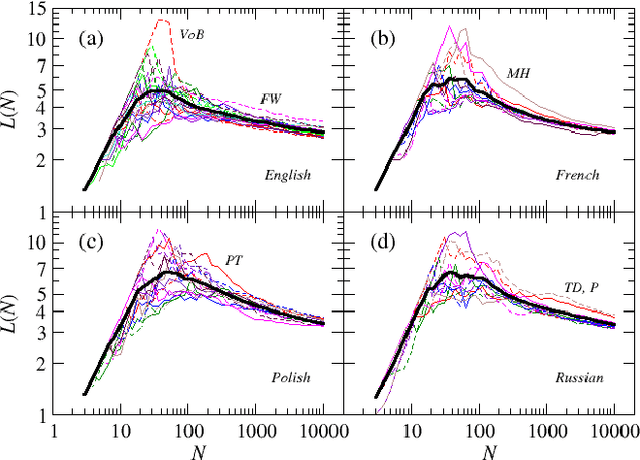
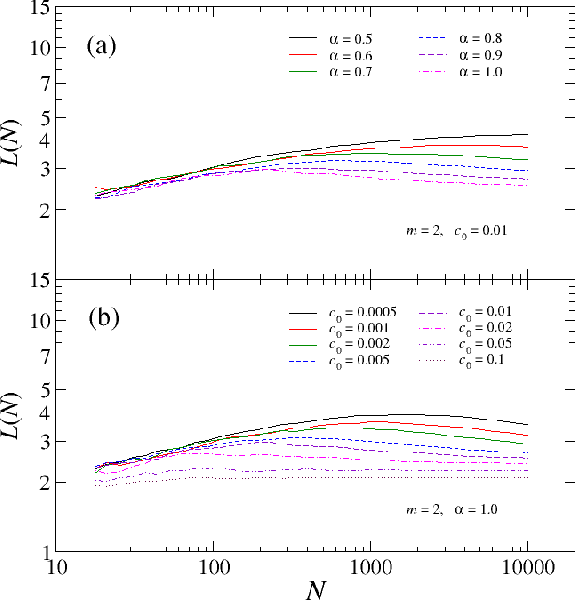
We investigate properties of evolving linguistic networks defined by the word-adjacency relation. Such networks belong to the category of networks with accelerated growth but their shortest path length appears to reveal the network size dependence of different functional form than the ones known so far. We thus compare the networks created from literary texts with their artificial substitutes based on different variants of the Dorogovtsev-Mendes model and observe that none of them is able to properly simulate the novel asymptotics of the shortest path length. Then, we identify the local chain-like linear growth induced by grammar and style as a missing element in this model and extend it by incorporating such effects. It is in this way that a satisfactory agreement with the empirical result is obtained.

Multifractal analysis of sentence lengths in English literary texts

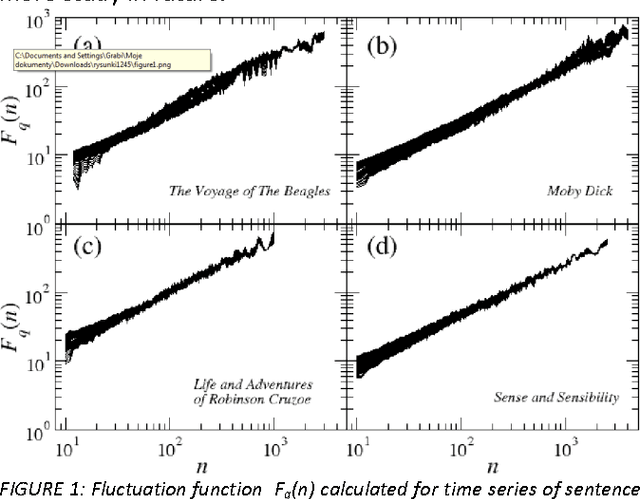
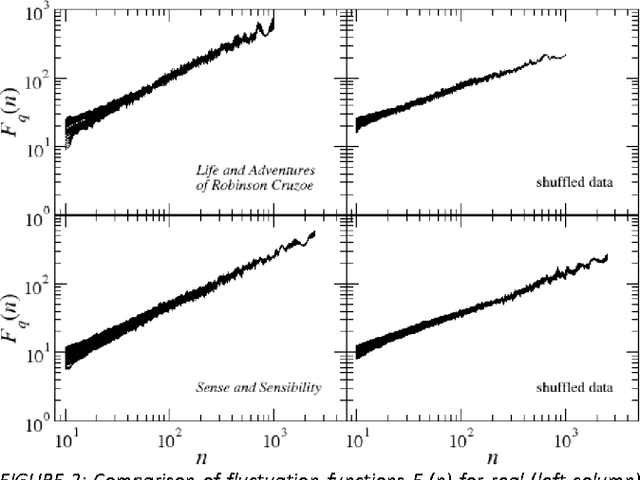
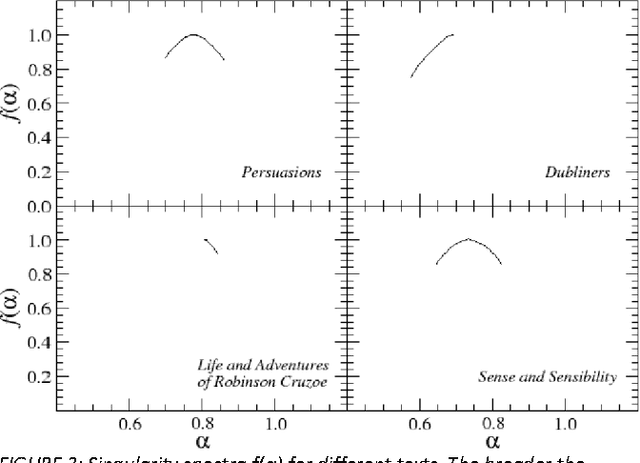
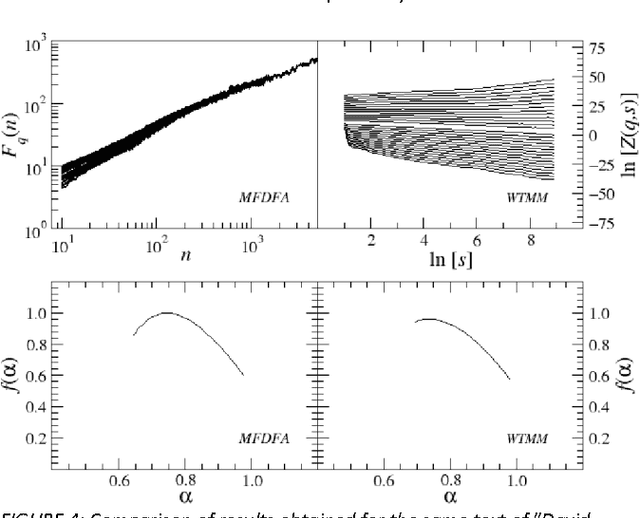
This paper presents analysis of 30 literary texts written in English by different authors. For each text, there were created time series representing length of sentences in words and analyzed its fractal properties using two methods of multifractal analysis: MFDFA and WTMM. Both methods showed that there are texts which can be considered multifractal in this representation but a majority of texts are not multifractal or even not fractal at all. Out of 30 books, only a few have so-correlated lengths of consecutive sentences that the analyzed signals can be interpreted as real multifractals. An interesting direction for future investigations would be identifying what are the specific features which cause certain texts to be multifractal and other to be monofractal or even not fractal at all.