Universal features of mountain ridge patterns on Earth

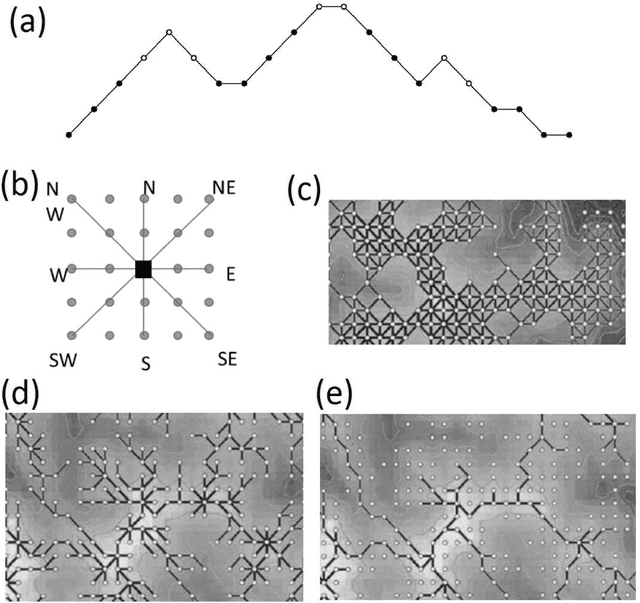
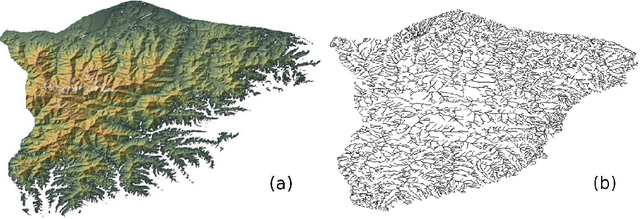
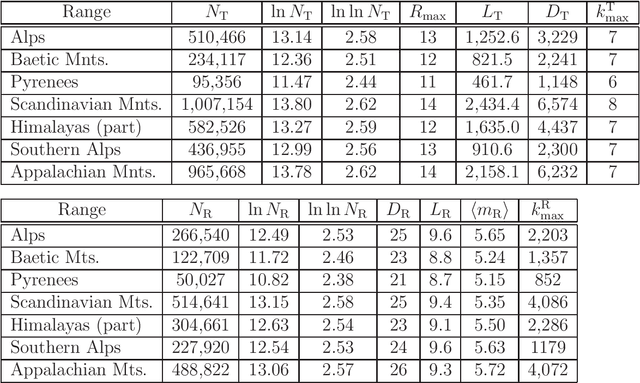
We study structure of the mountain ridge systems based on the empirical elevation data collected by Shuttle Radar Topography Mission (SRTM). We consider several prominent mountain ranges from different geological periods and different geographical locations: the Alps, the Pyrenees, the Baetic Mountains, the Scandinavian Mountains, the Southern Alps, the Appalachian Mountains, and a part of the Himalayas. By using a network-based approach, for each mountain range we construct a simple "topographic" network representation (i.e., the ridge junctions as nodes and the ridges connecting them as edges) as well as a "ridge" representation (i.e., the ridges as nodes and the ridge junctions as edges). Then we calculate the main parameters characterizing these networks, like the node degree distribution and the average shortest path length. We observe that the topographic networks inherit the fractal structure of the mountain ranges but do not show any other complex features. In contrast, the ridge networks, while lacking the proper fractality, reveal the power-law cumulative degree distributions (cdfs) with a scaling exponent $1.6 \le \beta \le 1.7$. By taking into account the fact that the analyzed mountains differ in many properties, like their area, height, age, and geological origin, these values of $\beta$ seem to be universal for the earthly mountainous terrain.

Modeling the average shortest path length in growth of word-adjacency networks

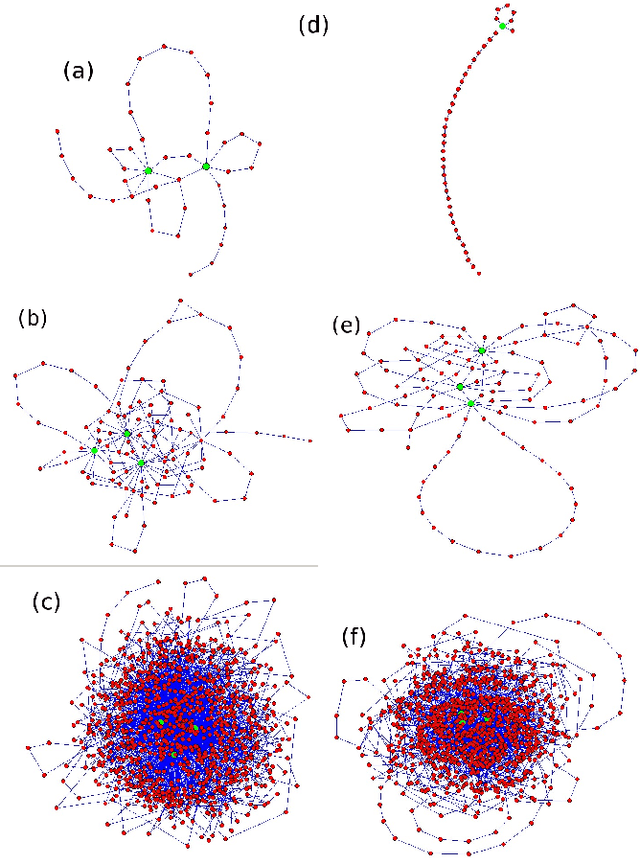
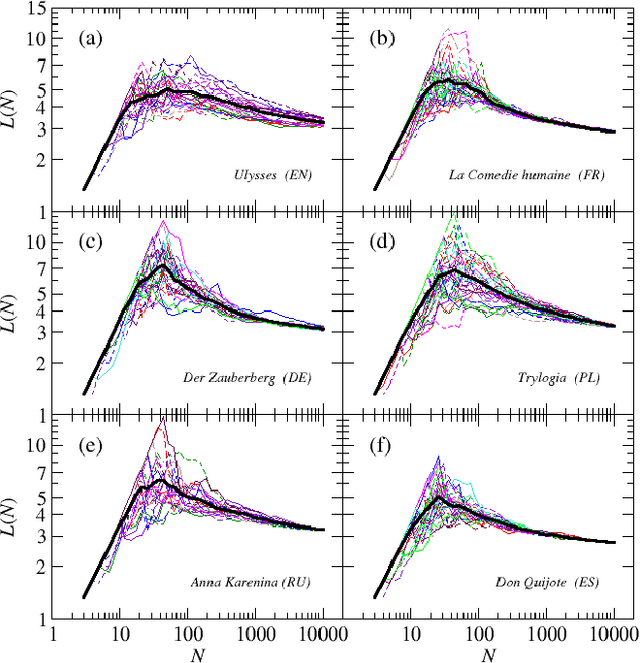
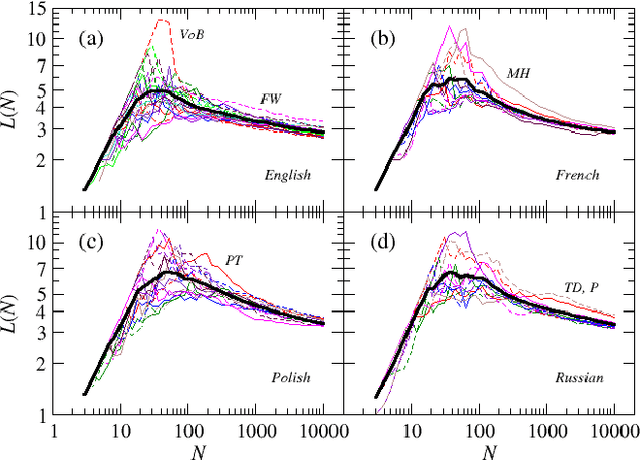
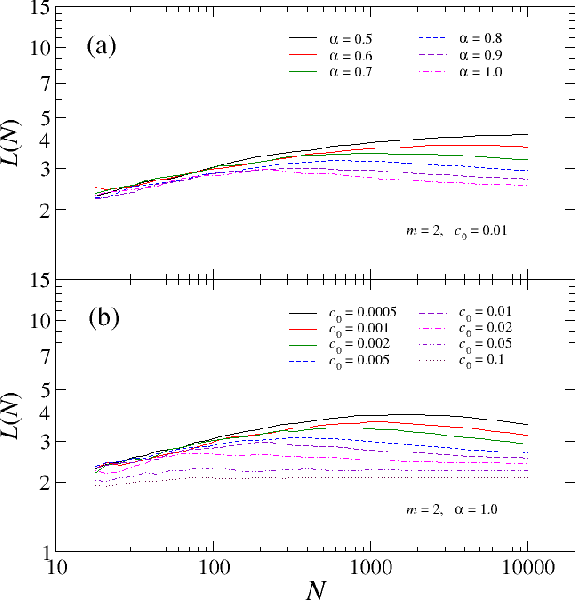
We investigate properties of evolving linguistic networks defined by the word-adjacency relation. Such networks belong to the category of networks with accelerated growth but their shortest path length appears to reveal the network size dependence of different functional form than the ones known so far. We thus compare the networks created from literary texts with their artificial substitutes based on different variants of the Dorogovtsev-Mendes model and observe that none of them is able to properly simulate the novel asymptotics of the shortest path length. Then, we identify the local chain-like linear growth induced by grammar and style as a missing element in this model and extend it by incorporating such effects. It is in this way that a satisfactory agreement with the empirical result is obtained.