Universal features of mountain ridge patterns on Earth

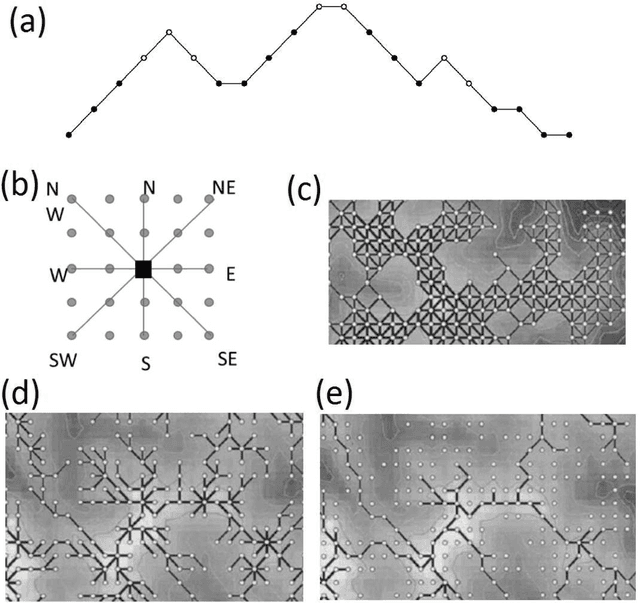
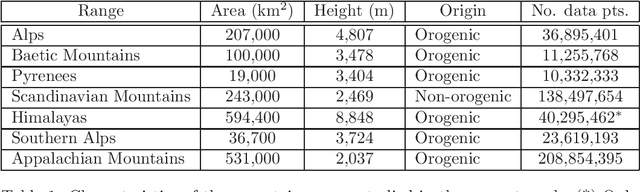
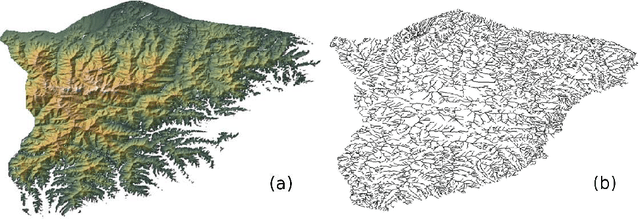
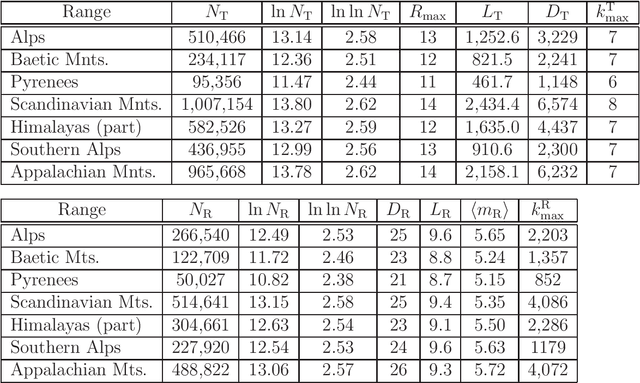
We study structure of the mountain ridge systems based on the empirical elevation data collected by Shuttle Radar Topography Mission (SRTM). We consider several prominent mountain ranges from different geological periods and different geographical locations: the Alps, the Pyrenees, the Baetic Mountains, the Scandinavian Mountains, the Southern Alps, the Appalachian Mountains, and a part of the Himalayas. By using a network-based approach, for each mountain range we construct a simple "topographic" network representation (i.e., the ridge junctions as nodes and the ridges connecting them as edges) as well as a "ridge" representation (i.e., the ridges as nodes and the ridge junctions as edges). Then we calculate the main parameters characterizing these networks, like the node degree distribution and the average shortest path length. We observe that the topographic networks inherit the fractal structure of the mountain ranges but do not show any other complex features. In contrast, the ridge networks, while lacking the proper fractality, reveal the power-law cumulative degree distributions (cdfs) with a scaling exponent $1.6 \le \beta \le 1.7$. By taking into account the fact that the analyzed mountains differ in many properties, like their area, height, age, and geological origin, these values of $\beta$ seem to be universal for the earthly mountainous terrain.