Marek Stanuszek
Quantifying origin and character of long-range correlations in narrative texts
Oct 14, 2015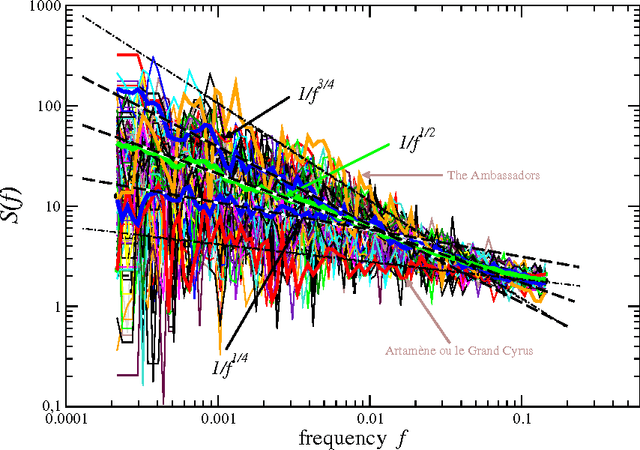
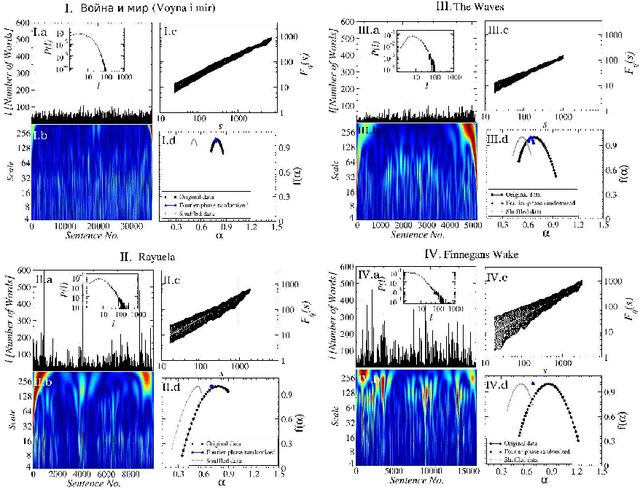
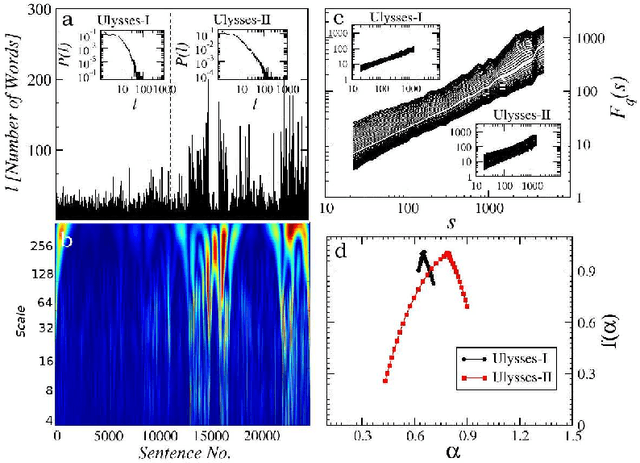
Abstract:In natural language using short sentences is considered efficient for communication. However, a text composed exclusively of such sentences looks technical and reads boring. A text composed of long ones, on the other hand, demands significantly more effort for comprehension. Studying characteristics of the sentence length variability (SLV) in a large corpus of world-famous literary texts shows that an appealing and aesthetic optimum appears somewhere in between and involves selfsimilar, cascade-like alternation of various lengths sentences. A related quantitative observation is that the power spectra S(f) of thus characterized SLV universally develop a convincing `1/f^beta' scaling with the average exponent beta =~ 1/2, close to what has been identified before in musical compositions or in the brain waves. An overwhelming majority of the studied texts simply obeys such fractal attributes but especially spectacular in this respect are hypertext-like, "stream of consciousness" novels. In addition, they appear to develop structures characteristic of irreducibly interwoven sets of fractals called multifractals. Scaling of S(f) in the present context implies existence of the long-range correlations in texts and appearance of multifractality indicates that they carry even a nonlinear component. A distinct role of the full stops in inducing the long-range correlations in texts is evidenced by the fact that the above quantitative characteristics on the long-range correlations manifest themselves in variation of the full stops recurrence times along texts, thus in SLV, but to a much lesser degree in the recurrence times of the most frequent words. In this latter case the nonlinear correlations, thus multifractality, disappear even completely for all the texts considered. Treated as one extra word, the full stops at the same time appear to obey the Zipfian rank-frequency distribution, however.
* 28 pages, 8 figures, accepted for publication in Information Sciences
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge