Finding Maximum Independent Sets in Dynamic Graphs using Unsupervised Learning

We present the first unsupervised learning model for finding Maximum Independent Sets (MaxIS) in dynamic graphs where edges change over time. Our method combines structural learning from graph neural networks (GNNs) with a learned distributed update mechanism that, given an edge addition or deletion event, modifies nodes' internal memories and infers their MaxIS membership in a single, parallel step. We parameterize our model by the update mechanism's radius and investigate the resulting performance-runtime tradeoffs for various dynamic graph topologies. We evaluate our model against state-of-the-art MaxIS methods for static graphs, including a mixed integer programming solver, deterministic rule-based algorithms, and a heuristic learning framework based on dynamic programming and GNNs. Across synthetic and real-world dynamic graphs of 100-10,000 nodes, our model achieves competitive approximation ratios with excellent scalability; on large graphs, it significantly outperforms the state-of-the-art heuristic learning framework in solution quality, runtime, and memory usage. Our model generalizes well on graphs 100x larger than the ones used for training, achieving performance at par with both a greedy technique and a commercial mixed integer programming solver while running 1.5-23x faster than greedy.

Distributed Online Rollout for Multivehicle Routing in Unmapped Environments

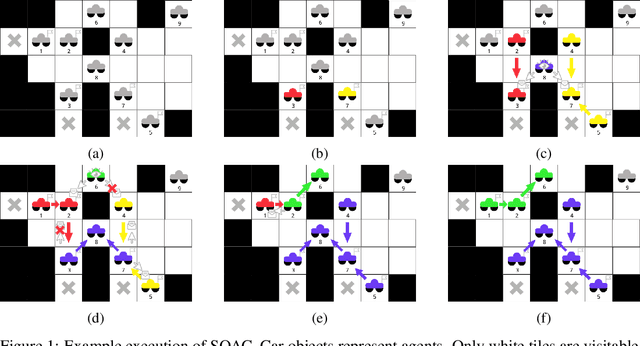
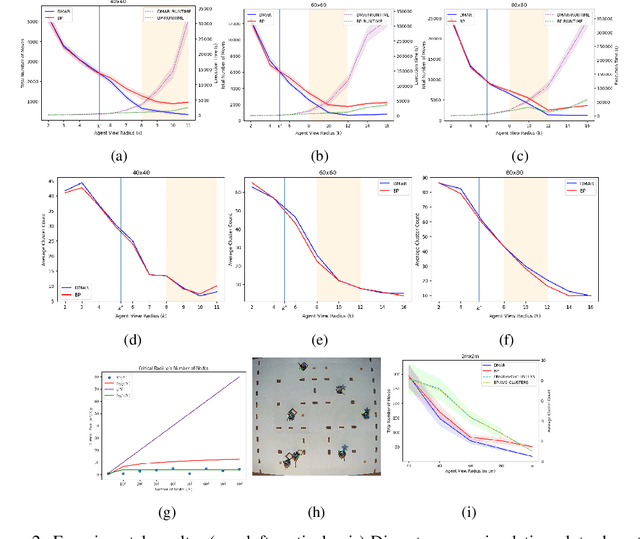
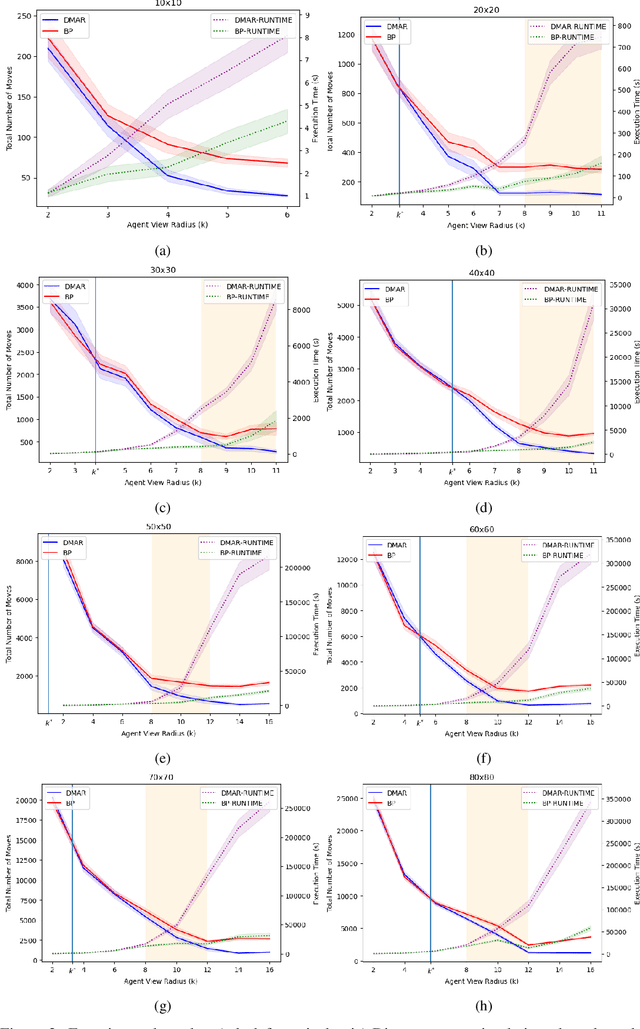
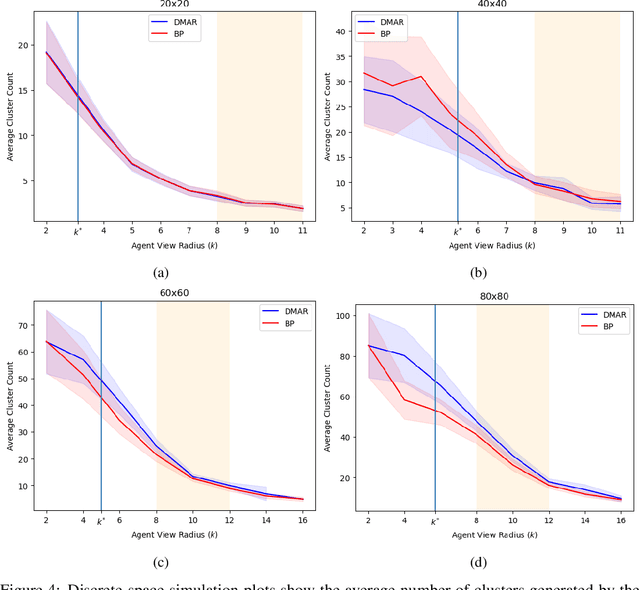
In this work we consider a generalization of the well-known multivehicle routing problem: given a network, a set of agents occupying a subset of its nodes, and a set of tasks, we seek a minimum cost sequence of movements subject to the constraint that each task is visited by some agent at least once. The classical version of this problem assumes a central computational server that observes the entire state of the system perfectly and directs individual agents according to a centralized control scheme. In contrast, we assume that there is no centralized server and that each agent is an individual processor with no a priori knowledge of the underlying network (including task and agent locations). Moreover, our agents possess strictly local communication and sensing capabilities (restricted to a fixed radius around their respective locations), aligning more closely with several real-world multiagent applications. These restrictions introduce many challenges that are overcome through local information sharing and direct coordination between agents. We present a fully distributed, online, and scalable reinforcement learning algorithm for this problem whereby agents self-organize into local clusters and independently apply a multiagent rollout scheme locally to each cluster. We demonstrate empirically via extensive simulations that there exists a critical sensing radius beyond which the distributed rollout algorithm begins to improve over a greedy base policy. This critical sensing radius grows proportionally to the $\log^*$ function of the size of the network, and is, therefore, a small constant for any relevant network. Our decentralized reinforcement learning algorithm achieves approximately a factor of two cost improvement over the base policy for a range of radii bounded from below and above by two and three times the critical sensing radius, respectively.

Asynchronous Deterministic Leader Election in Three-Dimensional Programmable Matter

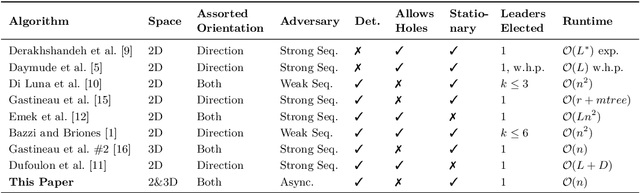
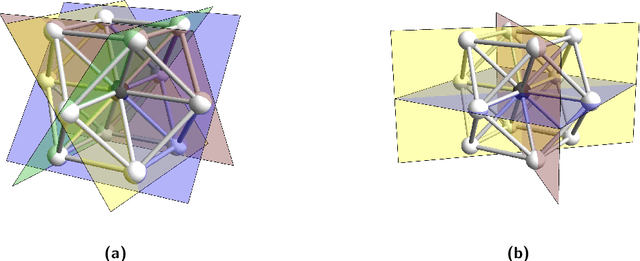
Over three decades of scientific endeavors to realize programmable matter, a substance that can change its physical properties based on user input or responses to its environment, there have been many advances in both the engineering of modular robotic systems and the corresponding algorithmic theory of collective behavior. However, while the design of modular robots routinely addresses the challenges of realistic three-dimensional (3D) space, algorithmic theory remains largely focused on 2D abstractions such as planes and planar graphs. In this work, we present the 3D geometric space variant for the well-established amoebot model of programmable matter, using the face-centered cubic (FCC) lattice to represent space and define local spatial orientations. We then give a distributed algorithm for the classical problem of leader election that can be applied to 2D or 3D geometric amoebot systems, proving that it deterministically elects exactly one leader in $\mathcal{O}(n)$ rounds under an unfair sequential adversary, where $n$ is the number of amoebots in the system. We conclude by demonstrating how this algorithm can be transformed using the concurrency control framework for amoebot algorithms (DISC 2021) to obtain the first known amoebot algorithm, both in 2D and 3D space, to solve leader election under an unfair asynchronous adversary.

Deadlock and Noise in Self-Organized Aggregation Without Computation

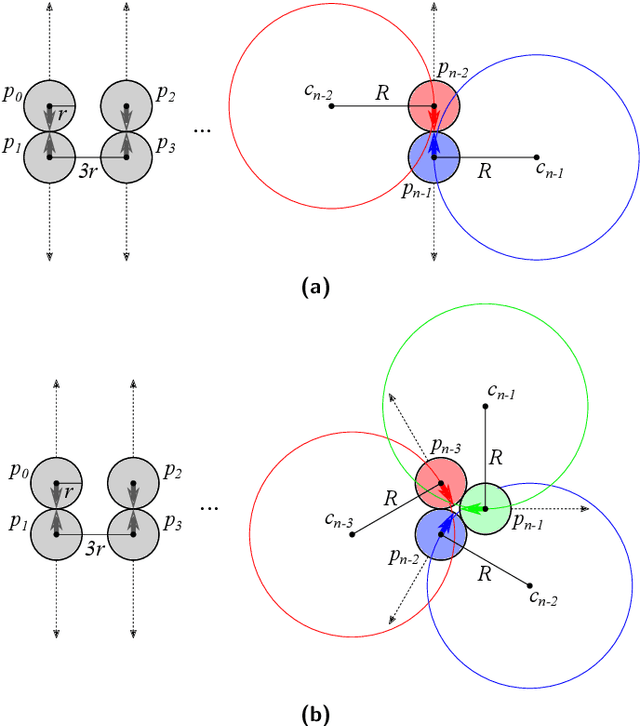
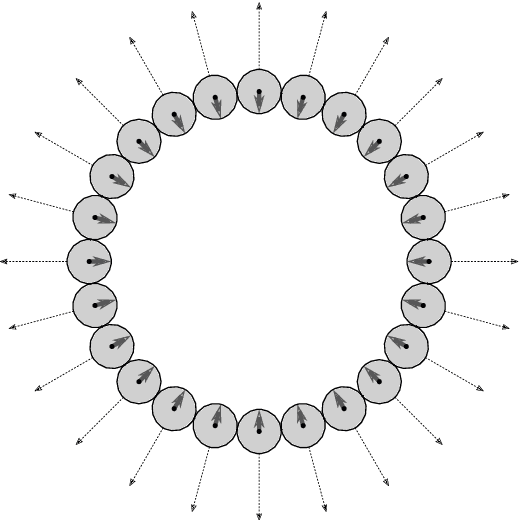
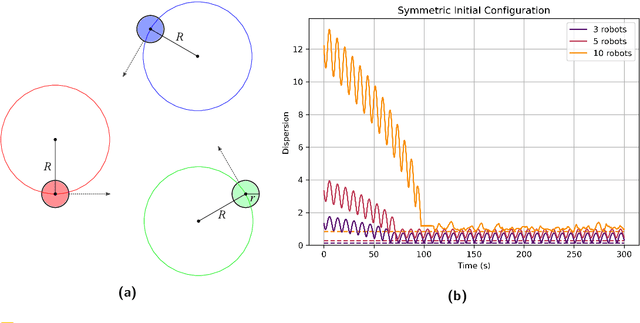
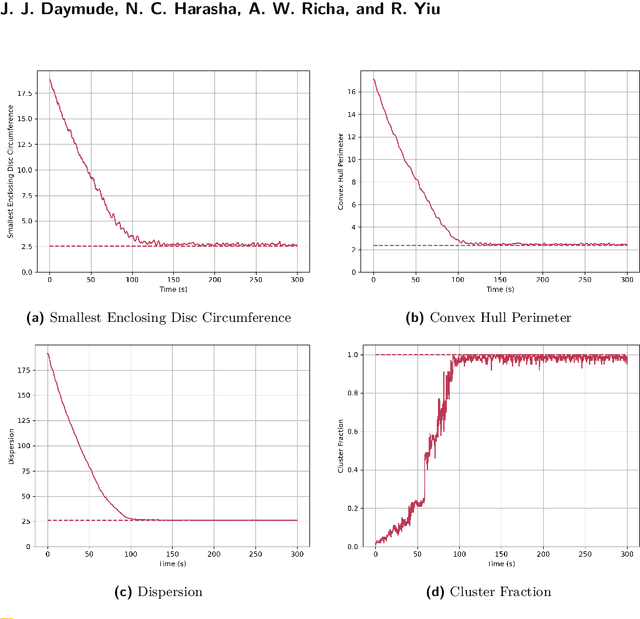
Aggregation is a fundamental behavior for swarm robotics that requires a system to gather together in a compact, connected cluster. In 2014, Gauci et al. proposed a surprising algorithm that reliably achieves swarm aggregation using only a binary line-of-sight sensor and no arithmetic computation or persistent memory. It has been rigorously proven that this algorithm will aggregate one robot to another, but it remained open whether it would always aggregate a system of $n > 2$ robots as was observed in experiments and simulations. We prove that there exist deadlocked configurations from which this algorithm cannot achieve aggregation for $n > 3$ robots when the robots' motion is uniform and deterministic. On the positive side, we show that the algorithm (i) is robust to small amounts of error, enabling deadlock avoidance, and (ii) provably achieves a linear runtime speedup for the $n = 2$ case when using a cone-of-sight sensor. Finally, we introduce a noisy, discrete adaptation of this algorithm that is more amenable to rigorous analysis of noise and whose simulation results align qualitatively with the original, continuous algorithm.

The Canonical Amoebot Model: Algorithms and Concurrency Control

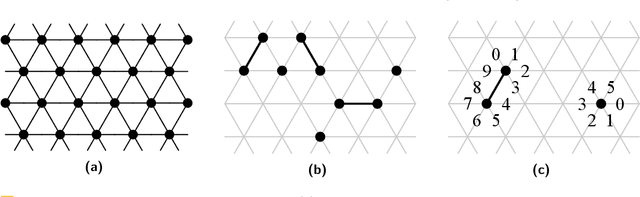
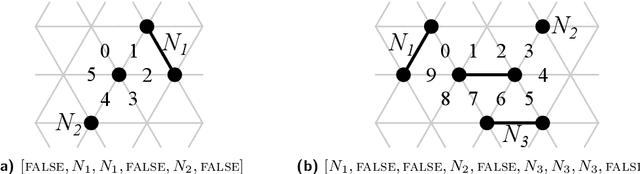
The amoebot model abstracts active programmable matter as a collection of simple computational elements called amoebots that interact locally to collectively achieve tasks of coordination and movement. Since its introduction (SPAA 2014), a growing body of literature has adapted its assumptions for a variety of problems; however, without a standardized hierarchy of assumptions, precise systematic comparison of results under the amoebot model is difficult. We propose the canonical amoebot model, an updated formalization that distinguishes between core model features and families of assumption variants. A key improvement addressed by the canonical amoebot model is concurrency. Much of the existing literature implicitly assumes amoebot actions are isolated and reliable, reducing analysis to the sequential setting where at most one amoebot is active at a time. However, real programmable matter systems are concurrent. The canonical amoebot model formalizes all amoebot communication as message passing, leveraging adversarial activation models of concurrent executions. Under this granular treatment of time, we take two complementary approaches to concurrent algorithm design. In the first, using hexagon formation as a case study, we establish a set of sufficient conditions that guarantee an algorithm's correctness under any concurrent execution, embedding concurrency control directly in algorithm design. In the second, we present a concurrency control protocol that uses locks to convert amoebot algorithms that terminate in the sequential setting and satisfy certain conventions into algorithms that exhibit equivalent behavior in the concurrent setting. These complementary approaches to concurrent algorithm design under the canonical amoebot model open new directions for distributed computing research on programmable matter and form a rigorous foundation for connections to related literature.

Programming Active Granular Matter with Mechanically Induced Phase Changes

Emergent behavior of particles on a lattice has been analyzed extensively in mathematics with possible analogies to physical phenomena such as clustering in colloidal systems. While there exists a rich pool of interesting results, most are yet to be explored physically due to the lack of experimental validation. Here we show how the individual moves of robotic agents are tightly mapped to a discrete algorithm and the emergent behaviors such as clustering are as predicted by the analysis of this algorithm. Taking advantage of the algorithmic perspective, we further designed robotic controls to manipulate the clustering behavior and show the potential for useful applications such as the transport of obstacles.

Bio-Inspired Energy Distribution for Programmable Matter

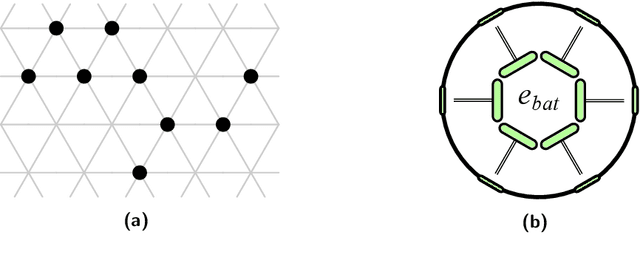
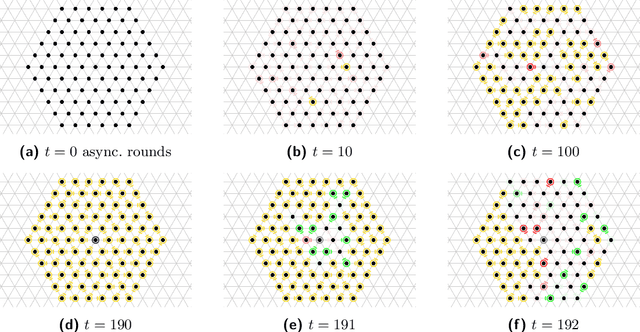
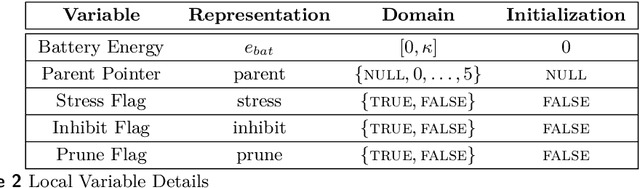
In systems of active programmable matter, individual modules require a constant supply of energy to participate in the system's collective behavior. These systems are often powered by an external energy source accessible by at least one module and rely on module-to-module power transfer to distribute energy throughout the system. While much effort has gone into addressing challenging aspects of power management in programmable matter hardware, algorithmic theory for programmable matter has largely ignored the impact of energy usage and distribution on algorithm feasibility and efficiency. In this work, we present an algorithm for energy distribution in the amoebot model inspired by the growth behavior of Bacillus subtilis bacterial biofilms. These bacteria use chemical signaling to communicate their metabolic states and regulate nutrient consumption throughout the biofilm, ensuring that all bacteria receive the nutrients they need. Our algorithm similarly uses communication to inhibit energy usage when there are starving modules, enabling all modules to receive sufficient energy to meet their demands. As a supporting but independent result, we extend the amoebot model's well-established spanning forest primitive so that it self-stabilizes in the presence of crash failures. We conclude by showing how this self-stabilizing primitive can be leveraged to compose our energy distribution algorithm with existing amoebot model algorithms, effectively generalizing previous work to also consider energy constraints.