The Canonical Amoebot Model: Algorithms and Concurrency Control
Paper and Code
May 06, 2021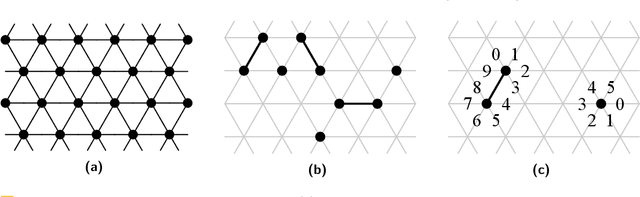


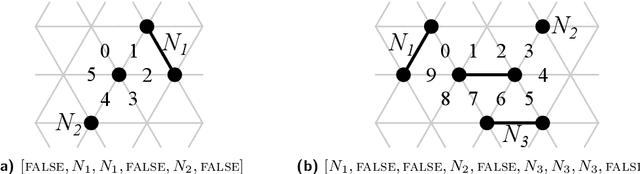
The amoebot model abstracts active programmable matter as a collection of simple computational elements called amoebots that interact locally to collectively achieve tasks of coordination and movement. Since its introduction (SPAA 2014), a growing body of literature has adapted its assumptions for a variety of problems; however, without a standardized hierarchy of assumptions, precise systematic comparison of results under the amoebot model is difficult. We propose the canonical amoebot model, an updated formalization that distinguishes between core model features and families of assumption variants. A key improvement addressed by the canonical amoebot model is concurrency. Much of the existing literature implicitly assumes amoebot actions are isolated and reliable, reducing analysis to the sequential setting where at most one amoebot is active at a time. However, real programmable matter systems are concurrent. The canonical amoebot model formalizes all amoebot communication as message passing, leveraging adversarial activation models of concurrent executions. Under this granular treatment of time, we take two complementary approaches to concurrent algorithm design. In the first, using hexagon formation as a case study, we establish a set of sufficient conditions that guarantee an algorithm's correctness under any concurrent execution, embedding concurrency control directly in algorithm design. In the second, we present a concurrency control protocol that uses locks to convert amoebot algorithms that terminate in the sequential setting and satisfy certain conventions into algorithms that exhibit equivalent behavior in the concurrent setting. These complementary approaches to concurrent algorithm design under the canonical amoebot model open new directions for distributed computing research on programmable matter and form a rigorous foundation for connections to related literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge